Intuitive

In this theory, the quantum particle (be it a photon, a positron, an electron, and so on) goes from an initial event to a (nearby) later event along each and every path - there’s an infinity of them (shades of Huygens Principle). The final amplitude is found by adding up the contributions from all these alternative paths. However, as the different paths have different lengths, then the phase-advance will be different and not necessarily equal to a whole number of wavelengths, and so the waves will not arrive instep. Only a very few nearby paths will add coherently and contribute significantly to the final amplitude; most paths will add destructively and yield no net contribution. (As Freeman Dyson reported it: “Dick Feynman told me. . . “The electron does anything it likes. . . It just goes in any direction at any speed. . . however it likes, and then you add up the amplitude and it gives you the wave-function.” I said to him, “You’re crazy.” But he wasn’t.”) Feynman’s beautifully simple theory not only agrees very precisely with experiment but explains away the teleological objection - that the particle doesn’t ‘know’ which path to follow - wrong, it follows all paths. Also, the theory goes over into the classical limit: for massive particles, say, a football moving at 10 ms$^{–1}$, the wavelength is so miniscule (around $10^{-34}$ m) that there isn’t the remotest hope for paths to interfere constructively - only one path survives, the very path predicted by the Principle of Least Action.

The Lazy Universe by Coopersmith

Origin of the Path Integral

The path integral idea emerges naturally when we consider what happens when we have many double slit experiments in a row:

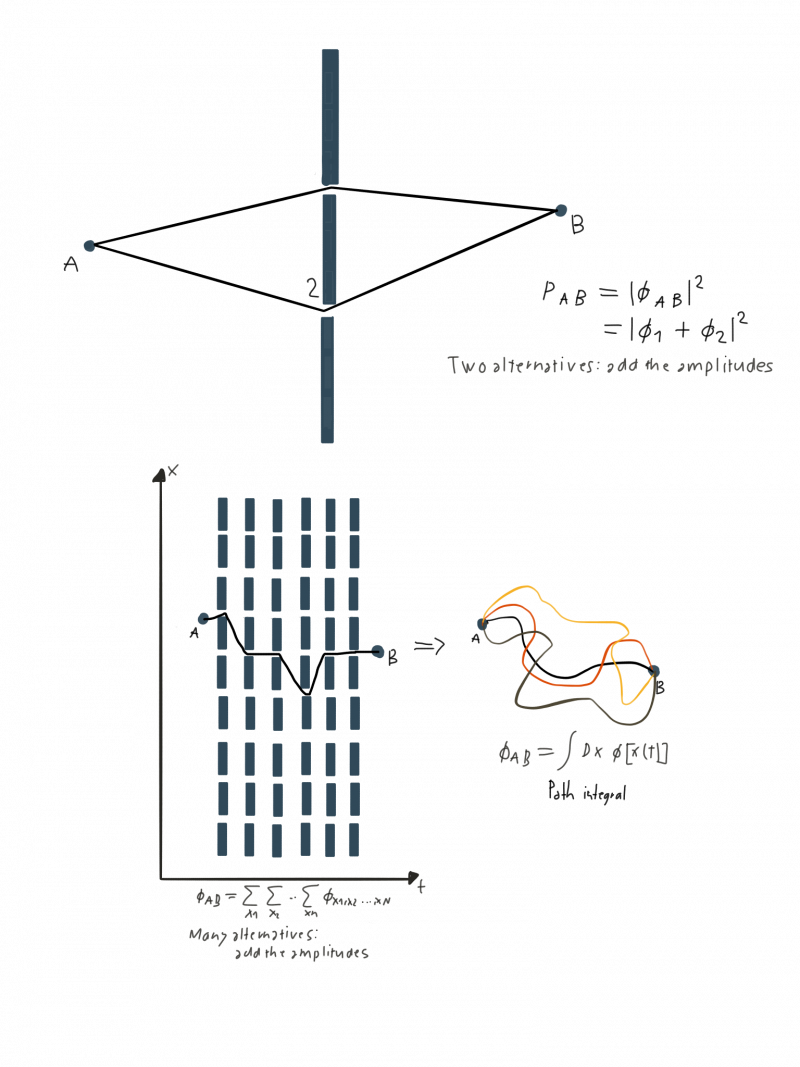
Recall the famous double-slit experiment in quantum mechanics, in which a beam of electrons is fired through two slits. If the electrons are classical particles like tiny balls, then we should expect the screen to have two bright strips corresponding to where the electrons hit, i.e. we would not expect interference pattern, which is a characteristic of wave. However, when the experiment is conducted, we observe interference pattern { electrons do have wave properties! It is not that the electrons are interfering with each other and thus somehow cause the interference pattern, since by firing the electrons one at a time, interference pattern still build up gradually as more and more electrons go through the slits. Quantum mechanically, we often say that the wave function will be the sum of two possible states: one that passes through slit A and one that passes through slit B, and the wave function is in a superposition of states. However there is no reason why we should stop at two slits, we could have three, and then the wave function will be the sum of three possible states. We can also have more than one screen. Therefore we could have say first screen with 2 slits, second screen with 3 slits etc. and stack them all together. That is, we have to consider all the probabilities of particle passing through the i-th slit of the k-th screen. Now imagine that we increase the number of screens and the number of slits and continue to do so in the limit towards infinity. In the limit with infinitely many slits, the slits are not there anymore! Therefore we reached a seemingly absurd [what isn’t in quantum mechanics?] conclusion that even in empty space without physical screens, we have to consider the probabilities of the particles taking all possible paths from one point to another instead of just the classical path [which is the unique path determined by solving differential equation of the Newtonian equation of motion given some initial condition.] As Zee described it, this is almost Zen. Where is the Commutation Relation Hiding in the Path Integral Formulation by Yen Chin Ong

Perhaps the best way to introduce the path integral formalism is by telling a story, certainly apocryphal as many physics stories are. Long ago, in a quantum mechanics class, the professor droned on and on about the double-slit experiment, giving the standard treatment. A particle emitted from a source S (fig. I.2.1) at time t = 0 passes through one or the other of two holes, $A_1$ and $A_2$ , drilled in a screen and is detected at time t = T by a detector located at O. The amplitude for detection is given by a fundamental postulate of quantum mechanics, the superposition principle, as the sum of the amplitude for the particle to propagate from the source S through the hole $A_1$ and then onward to the point O and the amplitude for the particle to propagate from the source S through the hole $A_2$ and then onward to the point O. Suddenly, a very bright student, let us call him Feynman, asked, “Professor, what if we drill a third hole in the screen?” The professor replied, “Clearly, the amplitude for the particle to be detected at the point O is now given by the sum of three amplitudes, the amplitude for the particle to propagate from the source S through the hole $A_1$ and then onward to the point O, the amplitude for the particle to propagate from the source S through the hole $A_2$ and then onward to the point O, and the amplitude for the particle to propagate from the source S through the hole A 3 and then onward to the point O.” The professor was just about ready to continue when Feynman interjected again, “What if I drill a fourth and a fifth hole in the screen?” Now the professor is visibly losing his patience: “All right, wise guy, I think it is obvious to the whole class that we just sum over all the holes.” To make what the professor said precise, denote the amplitude for the particle to propagate from the source S through the hole $A_i$ and then onward to the point O as A(S → A_i → O). Then the amplitude for the particle to be detected at the point O is

$$ A(\text{detected at O})= \sum_i A(S → A_i → O) $$

But Feynman persisted, “What if we now add another screen (fig. I.2.2) with some holes drilled in it?” The professor was really losing his patience: “Look, can’t you see that you just take the amplitude to go from the source S to the hole $A_i$ in the first screen, then to the hole $B_j$ in the second screen, then to the detector at O , and then sum over all i and j ?” Feynman continued to pester, “What if I put in a third screen, a fourth screen, eh? What if I put in a screen and drill an infinite number of holes in it so that the screen is no longer there?” The professor sighed, “Let’s move on; there is a lot of material to cover in this course.”

But dear reader, surely you see what that wise guy Feynman was driving at. I especially enjoy his observation that if you put in a screen and drill an infinite number of holes in it, then that screen is not really there. Very Zen! What Feynman showed is that even if there were just empty space between the source and the detector, the amplitude for the particle to propagate from the source to the detector is the sum of the amplitudes for the particle to go through each one of the holes in each one of the (nonexistent) screens. In other words, we have to sum over the amplitude for the particle to propagate from the source to the detector following all possible paths between the source and the detector (fig. I.2.3).

$$A(\text{particle to go from S to O in time T} ) = $$ $$\sum_{\text{paths}} ( \text{A particle to go from S to O in time T following a particular path }) $$

Page 7 in QFT in a Nutshell by A. Zee

• A perfect layman explanation of the path integral formalism can be found in the book Quantum Electrodynamics by Richard P. Feynman
• See also: https://gravityandlevity.wordpress.com/2009/08/05/the-path-integral-calculating-the-future-from-an-unknown-past/
• http://www.thephysicsmill.com/2013/07/16/reality-is-the-feynman-path-integral/

Concrete

In the path integral formalism, we calculate the probability that a particle, which starts at some point $S$, ends up at some point $P$, by summing over all possible paths that connect $S$ and $P$.

For each path, we can calculate a probability amplitude $A_i$. To get the total probability that the particle ends up at $P$, we sum over all these amplitudes $A_i$ and then square the result.

Each amplitude is basically a complex number and thus can be represented by an arrow in the complex plane.

Recommended Resources:

• Path Integrals in Quantum Theories: A Pedagogic First Step by R. Klauber
• Teaching quantum physics by the sum over paths approach and GeoGebra simulations M Malgier et. al
• Path Integral Methods and Applications by Richard MacKenzie
• The physics behind path integrals in quantum mechanics by Phillip D. Mannheim
• http://www.quantumfieldtheory.info/website_Chap18.pdf
• http://www.physics.umd.edu/courses/Phys851/Luty/notes/pathint.pdf
• http://qu-bit.narod.ru/texts/feynman.pdf
• Shankar, Principles of QM, the Chapter "Path integrals revisited" is especially useful for students interested in condensed matter physics.
• Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets by H. Kleinert is the bible on path integrals.
• Majorana and the path-integral approach to Quantum Mechanics by S. Esposito, Annales de la Fondation Louis de Broglie, Volume 31 no 2-3, pp. 207-225, 2006

The path integral formalism is what we get when we apply the Lagrangian framework to quantum mechanics. This is described, for example, here.

Abstract

The use of Feynman path integrals in physics has been an extremely useful heuristic. From time to time, people ask, whether these integrals can be made rigorous, in the sense that they are defined by an underlying measure on path-space. The answer is that, even in the Gaussian case, there is no such measure. This is known as Cameron's theorem. It means that the usual manipulations of integral calculus, such as changing the order of integrations (Fubini's theorem), or differentiation under the integral sign, might give wrong answers. Often, the answer given by a Gaussian Feynman integral is correct. In such a case, one might find a justification by introducing concepts such the promeasures of Cecile deWitt-Morette. A more general method, which works in quantum field theories of space-time dimension 3, is to adopt a euclidean approach, in which functions are analytically continued to imaginary time, as in Glimm and Jaffe. This converts the Feynman integral to a Wiener integral (which does exist); the integrals can then be defined; physics then has to be recovered by analytic continuation back to real space-time, and the proof that this is possible is one of the harder parts of the analysis.Lost Causes in Theoretical Physics by Streater

• Glimm, J. & Jaffe, A. [1981] Quantum Physics. A Functional Integral Point of View. (Springer Verlag, New York).
• C. Grosche: An introduction into the Feynman path integral, preprint hep-th/9302097; C. Grosche, F. Steiner, Handbook of Feynman path integrals, Springer tracts in modern physics 145, Springer-Verlag, Berlin, 1998

For a possible physical interpretation of the path integral in terms of Random Walks, see

• https://arxiv.org/abs/quant-ph/0109092
• https://arxiv.org/abs/quant-ph/0206016
• https://arxiv.org/abs/quant-ph/0411005
• http://www.brannenworks.com/plavchan_feynmancheckerboard.pdf

Why is it interesting?

The path integral is extremely useful to understand global properties of a system in quantum field theory.

In addition to these standard applications, the path integral is also somewhat popular in quantitative finance.

One of the great advantages of the path integral formulation of quantum mechanics and field theory is the possibility of identifying nonperturbatively the stationary configurations that dominate the action and thereby identify and understand the essential physics of complex systems with many degrees of freedom.

Instantons, the QCD Vacuum, and Hadronic Physics ∗ J. W. Negele

One of the major advantages of the path integral representation of quantum mechanics is that it most transparently embodies the transition to classical mechanics, i.e. the semiclassical limit.

https://arxiv.org/pdf/hep-ph/0009136.pdf.

The most useful approach to the quantization of gauge theories appears to be Feynman's path integral method. From a geometric point of view, the path integral has the advantage of being able to take into account the global topology of the gauge potentials, while the canonical perturbation theory approach to quantization is sensitive only to the local topology.

http://home.fnal.gov/~leonardo/physicsnotes/notes/NotesInstantons.pdf

What do we learn from path integrals? As far as I am aware, path integrals give us no dramatic new results in the quantum mechanics of a single particle. Indeed, most if not all calculations in quantum mechanics which can be done by path integrals can be done with considerably greater ease using the standard formulations of quantum mechanics. (It is probably for this reason that path integrals are often left out of undergraduate-level quantum mechanics courses.) So why the fuss? As I will mention shortly, path integrals turn out to be considerably more useful in more complicated situations, such as field theory. But even if this were not the case, I believe that path integrals would be a very worthwhile contribution to our understanding of quantum mechanics. Firstly, they provide a physically extremely appealing and intuitive way of viewing quantum mechanics: anyone who can understand Young’s double slit experiment in optics should be able to understand the underlying ideas behind path integrals. Secondly, the classical limit of quantum mechanics can be understood in a particularly clean way via path integrals.

It is in quantum field theory, both relativistic and nonrelativistic, that path integrals (functional integrals is a more accurate term) play a much more important role, for several reasons. They provide a relatively easy road to quantization and to expressions for Green’s functions, which are closely related to amplitudes for physical processes such as scattering and decays of particles. The path integral treatment of gauge field theories (non-abelian ones, in particular) is very elegant: gauge fixing and ghosts appear quite effortlessly. Also, there are a whole host of nonperturbative phenomena such as solitons and instantons that are most easily viewed via path integrals. Furthermore, the close relation between statistical mechanics and quantum mechanics, or statistical field theory and quantum field theory, is plainly visible via path integrals. Path Integral Methods and Applications by Richard MacKenzie

The path integral formulation of quantum mechanics is the one in which one can see in the most natural and transparent way that the quantization of a given classical dynamical system depends often in a crucial way upon the global topological properties of the underlying configuration space. Indeed, the .propagator is expressed, roughly speaking, as a weighed sum over all possible paths connecting any two given points in configuration space. As the paths wander through all of the space, they also probe its topology.

Inequivalent Quantizations in Multiply Connected Spaces by P. A. HORVATHY et. al.

FAQ

How do particle arise in the path integral formulation?

See https://physics.stackexchange.com/questions/303984/particle-picture-in-the-path-integral-formulation-of-quantum-field-theory

Are the path integral formalism and the operator formalism inequivalent?

https://physics.stackexchange.com/questions/252213/are-the-path-integral-formalism-and-the-operator-formalism-inequivalent

Where are the canonical commutation relations hidden in the path integral formulation?

See Where is the Commutation Relation Hiding in the Path Integral Formulation by Yen Chin Ong

Why is the contribution of a path in Feynmans path integral formalism proportional to the action in the exponent?

see https://physics.stackexchange.com/questions/8663/why-is-the-contribution-of-a-path-in-feynmans-path-integral-formalism-sim-e

What's the physical Interpretation of the Integrand of the Feynman Path Integral?

see https://physics.stackexchange.com/questions/61139/physical-interpretation-of-the-integrand-of-the-feynman-path-integral/202298#202298

History

Thirty-one years ago, Dick Feynman told me about his ‘‘sum over histories’’ version of quantum mechanics. ‘‘The electron does anything it likes,’’ he said. ‘‘It just goes in any direction at any speed,… however it likes, and then you add up the amplitudes and it gives you the wavefunction.’’ I said to him, ‘‘You’re crazy.’’ But he wasn’t.

Freeman Dyson, 1980