Intuitive

Sometimes when people talk about ``quantization", what they really mean is discretization, i.e., a phenomenon where the constraints of the physical system have the effect that some physical quantity only appears in discrete jumps, while all values in between are physically forbidden.

The easiest example is a rope that is held under constant tension by two hands:

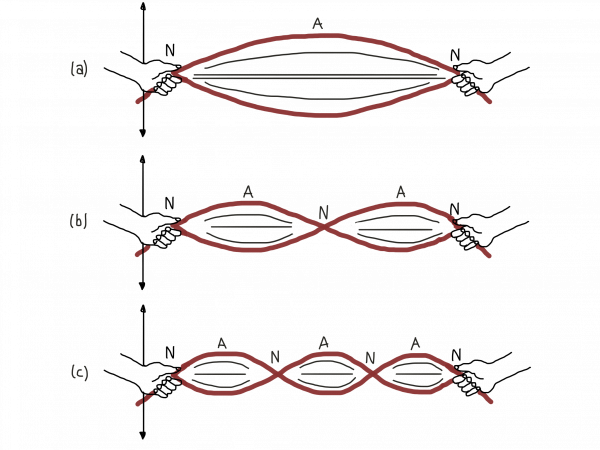
The thing is, no matter how the two hands try to make the rope vibrate, the rope will only vibrate with a quantized set of modes. The two hands fix the rope at both ends. As a result of this constraint, the rope can only vibrate with fixed frequencies. The frequencies between this fixed set of frequencies are physically impossible:

The same thing now happens also in quantum mechanics.

Here we describe particles using waves. If we then consider, for example, a particle in a box we notice that only a specific discrete set of wave functions are physically possible. Physically this means that the energy levels within the box are quantized in quantum mechanics, as a result of the constraints imposed by the box.

Quantization in the context of quantum mechanics

In quantum physics, quantization is the process of constructing the quantum formulation of a system from its classical description. Starting with a classical system, we wish to formulate a quantum theory, which in an appropriate limit, reduces back to the classical system.

The inverse procedure is called dequantization, or simply "taking the classical limit". Here we start with a quantum theory and arrive back at its classical counterpart.

After electrons and holes, the simplest example of the emergence of particles in rocks is sound quantization. This astonishing phenome­non is the closest thing to real magic I know. Sound is familiar to everyone as the vibration of elastic matter, typically air but also solid

Sound quantization is a particularly instructive example of parti­cle emergence because it can be worked out exactly, in all its detail, starting from the underlying laws of quantum mechanics obeyed by atoms-provided the atoms are first postulated to have perfectly crys­tallized. This is what we mean by quantized sound being a universal feature of crystallinity. This phenomenon is the prototypical example of Goldstone's theorem, the statement that particles necessarily emerge in any matter exhibiting spontaneous broken symmetry. The analysis also reveals that the particles of sound acquire more and more integrity as the corresponding tone is lowered in pitch, and become exact in the limit of low tone. Very high-pitched sound quanta propagating through a solid can decay probabilistically into two or more quanta of sound with a lower pitch, this decay being aptly anal­ogous to that of a radioactive nucleus or an elementary particle such as a pion. Their decay turns out to be the same thing as elastic nonlinearity—the failure of distortion of the solid to be proportional to the stress on it when the stress is large, such as occurs just before fracture. But these nonlinearities matter less and less as the sound wavelength increases, the time scale for the decay increases as the tone is lowered and eventually becomes infinite. Sound quantization is a beautiful case of magic in physics revealed by thoughtful analysis to be not magic at all but a failure of intuition.

The quantum properties of sound are identical to those of light. This fact is important, for it is not at all obvious, given that sound is a collective motion of elastic matter while light ostensibly is not. The analogy is revealed most simply and directly by heat capacity. The ability of crystalline insulators to store heat drops universally in cryo­genic environments as the cube of the temperature. This effect is a consequence of quantum mechanics, for it is easy to show that the heat capacity would have to be constant and large (as it is at room temperature) if all the atoms obeyed Newton's laws. The heat capacity of empty space follows the rule precisely. Space is not empty when it is heated of course, but filled with light, the color and intensity of which depend on the temperature. This effect is familiar from the red glow emitted from hot embers and the white light blazing from a light bulb filament or the surface of the sun. A warm crystal is likewise filled with sound.

In either case the specific temperature depen­dence of the heat capacity is accounted for quantitatively by the Planck law, a simple formula derived om the assumption that light or sound can be created or annihilated only in discrete amounts.8 In fact, the formula for the heat capacity of a crystalline solid is simply that of empty space, with the speed of sound Substituted for the speed of light.

The analogy between phonons and photons raises the obvious question of whether light itself might be emergent.

The similarity between sound and light requires explanation, for there is no obvious reason for their quantum mechanics to be the same. In the case of sound,quantization may be deduced om the underlying laws of quantum mechanics. In the case of light it must be postu­lated. This logical loose end is enormously embarrassing, and is some­thing we physicists prefer to disguise in formal language.

The emergent quantum of sound, known as a phonon,is aptly analogous to the quantum of light, the photon.

The similarity between sound and light requires explanation, for there is no obvious reason for their quantum mechanics to be the same. In the case of sound-quantization may be deduced from the underlying laws of quantum mechanics obeyed by the atoms. In the case of light it must be postu­lated. This logical loose end is enormously embarrassing, and is some­thing we physicists prefer to disguise in formal language. Thus we say that light and sound obey the Planck law by virtue of canonical quan­tization and the bosonic nature of the underlying degrees of freedom.But this is no explanation at all, for the reasoning is circular. Stripped of its complexity, "canonical quantization" simply boils down to re­quiring light to have properties modeled after those of sound.

Light has a vexing aspect, the gauge effect, that has no analogue in sound and is o en used to argue that light cannot be emergent. This argument is false, since there are plenty of ways one could imagine that light might emerge, but the effect is nonetheless a serious con­ceptual matter that points to an important physical distinction be­tween light and sound. Its simplest manifestation is in heat capacity.When a sound wave passes by, a given atom is displaced a bit om its static position in the lattice. There are three distinct ways it can do this-left-right, up-down, and forward-backward-each of which contributes separately to the heat capacity, effectively multiplyinG the final answer by three. But the corresponding multiplication factor for light is only two, even though light is also the displacement of something. On one of the three axes the stuff of the universe, what­ever it is, simply cannot vibrate-at least on time scales relevant to experimentally accessible temperatures-or store heat. The underly­ing microscopic reason is not known and is treated in modern physics as a postulate.

"A different Universe" by Robert Laughlin

Concrete

Canonical quantization means that we replace the classical Poisson brackets with commutator brackets

\begin{eqnarray} \text{Poisson bracket } \{\cdot,\cdot\} &\longrightarrow \text{commutator } i[\cdot,\cdot]\\ \end{eqnarray}

The procedure is called canonical because we are considering canonical variables here, e.g. the canonical momentum. A different way to describe a quantum theory is the path integral approach, which is also known as functional quantization.

Overview

Source: page 5 in Klauber's Student friendly QFT book

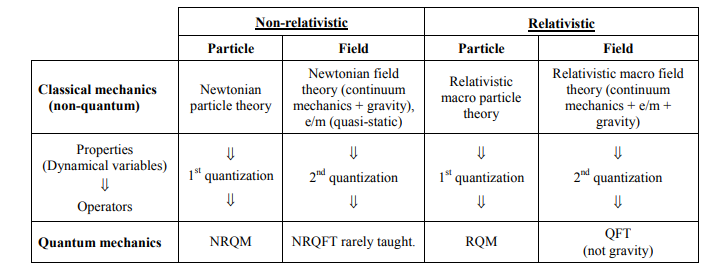
First Quantization = Quantization in Particle Theories

First quantization is used to get from a classical particle theory the corresponding quantum theory. The procedure can be summarized through the following two steps

1. We use the same Hamiltonian for the quantum particles that we would use if they were behaving classically.
2. We replace the classical Poisson brackets for conjugate variables with commutator brackets (divided by $i\hbar$): $$ \{q_i,p_j\} = \delta_{ij} \longrightarrow [\hat{q}_i,\hat{p}_j]= \hat{q}_i\hat{p}_j -\hat{p}_j \hat{q}_i = i \hbar \delta_{ij} $$

Now a crucial observation is that ordinary numbers and function commutate: $[f(x),g(x)]=0$ or also $[3,5]=3\cdot 5 - 5\cdot 3 =0$. Therefore, we learn here that the location $\hat{q}_i$ and the momentum $\hat{p}_j$ can no longer be mere numbers or functions, but must be operators. Operators are always denoted by a hat.

The operators are then interpreted as measurement operators. This means, for example, when we act with the momentum operator $\hat{p}_j$ on the wave function $\Psi$, which is the object that we use to describe, say a particle, we get as a result the momentum that the particle has in the $j$ direction: $\hat{p}_j \Psi = p_j \Psi$. (This only works so simple when the particle is in a momentum eigenstate, i.e. has a definite momentum. Otherwise the result is a superposition and more complicated.) For more on this, see the page about quantum mechanics.

Second Quantization = Quantization in Field Theories

Canonical second quantization works analogously:

1. We again use the same Hamiltonian for the quantum fields as if we were dealing with a classical field.
2. We replace the classical fields with operators and the Poisson brackets with commutators: $$i\{\phi_s(t,\vec{x},\pi_r(t,\vec{y}\} = \delta_{sr} \delta(\vec x - \vec y) \longrightarrow [\phi_s(t,\vec{x}),\pi_r(t,\vec{y}\,')]=i \hbar \delta_{sr} \delta(\vec{x}-\vec{y}\,') $$

Again these equation tell us that our dynamical variables, here the field and its conjugate momentum, are no long mere functions but instead operators. However, the interpretation of these operators is a bit more difficult and is best understood by looking at an explicit example.

The action functional $S[\phi(x)]$ for a free real scalar field of mass $m$ is \begin{eqnarray} S[\phi(x)]\equiv \int d^{4}x \,\mathcal{L}(\phi,\partial_{\mu}\phi)= {1\over 2}\int d^{4}x \,\left(\partial_{\mu}\phi\partial^{\mu}\phi- {m^{2}}\phi^2\right). \end{eqnarray} We can calculate the equations of motion are obtained by using the Euler-Lagrange equations \begin{eqnarray} \partial_{\mu}\left[\partial\mathcal{L}\over \partial(\partial_{\mu}\phi) \right]-{\partial\mathcal{L}\over \partial\phi}=0 \quad \Longrightarrow \quad (\partial_{\mu}\partial^{\mu}+m^{2})\phi=0. \label{eq:eomKG} \end{eqnarray}

The momentum canonically conjugated to the field $\phi(x)$ is given by \begin{eqnarray} \pi(x)\equiv {\partial\mathcal{L}\over \partial(\partial_{0}\phi)} ={\partial\phi\over\partial t}. \end{eqnarray}

We can solve the equations of motion by using the Fourier transform \begin{eqnarray} (\partial_{\mu}\partial^{\mu}+m^{2})\phi(x)=0 \quad \Longrightarrow \quad (-p^{2}+m^{2})\widetilde{\phi}(p)=0, \end{eqnarray} The general solution can then be written as \begin{eqnarray} \phi(x)&=&\int {d^{4}p\over (2\pi)^{4}}(2\pi)\delta(p^{2}-m^{2})\theta(p^{0}) \left[\alpha(p)e^{-ip\cdot x}+\alpha(p)^{*}e^{ip\cdot x}\right] \nonumber \\ &=& \int {d^{3}p\over (2\pi)^{3}}{1\over 2\omega_{p}} \left[\alpha(\vec{p}\,)e^{-i\omega_{p}t + \vec{p}\cdot \vec{x}} +\alpha(\vec{p}\,)^{*}e^{i\omega_{p}t-\vec{p}\cdot \vec{x}}\right] \label{eq:general_sol_phi} \end{eqnarray} The conjugate momentum is then \begin{eqnarray} \pi(x)= -{i\over 2}\int {d^{3}p\over (2\pi)^{3}} \left[\alpha(\vec{p}\,)e^{-i\omega_{p}t + \vec{p}\cdot \vec{x}} +\alpha(\vec{p}\,)^{*}e^{i\omega_{p}t-\vec{p}\cdot \vec{x}}\right]. \end{eqnarray}

Now $\phi(x)$ and $\pi(x)$ are promoted to operators by replacing the functions $\alpha(\vec{p})$, $\alpha(\vec{p})^{*}$ by the operators \begin{eqnarray} \alpha(\vec{p}\,)\longrightarrow \widehat{\alpha}(\vec{p}\,), \alpha(\vec{p}\,)^{*}\longrightarrow \widehat{\alpha}^{\dagger}(\vec{p}\,). \end{eqnarray} Moreover, demanding $[\phi(t,\vec{x}),\pi(t,\vec{x}\,')]= i\delta(\vec{x}-\vec{x}\,')$ tells us that the operators $\widehat{\alpha}(\vec{p})$, $\widehat{\alpha}(\vec{p})^{\dagger}$ fulfill the commutation relations

\begin{eqnarray} {}[\alpha(\vec{p}),\alpha^{\dagger}(\vec{p}\,')]&=&(2\pi)^{3} (2\omega_{p})\delta(\vec{p}-\vec{p}\,'), \nonumber \\ {}[\alpha(\vec{p}),\alpha(\vec{p}\,')] &=&[\alpha^{\dagger}(\vec{p}),\alpha^{\dagger}(\vec{p}\,')]=0. \end{eqnarray}

The interpretation of these operators is that they create particle. Concretely, we get a state describing a particle when we act with the creation operators $\alpha(\vec{p})$ on the vacuum state (=the state without any particle) $|0\rangle$ which satisfies \begin{eqnarray} \langle 0|0\rangle=1, \quad \widehat{P}^{\mu}|0\rangle=0, \quad \mathcal{U}(\Lambda)|0\rangle=|0\rangle, \quad \forall \Lambda \in {\rm SO}(1,3). \end{eqnarray} Therefore, we can write a general one-particle state $|f\rangle\in\mathcal{H}_{1}$ as \begin{eqnarray} |f\rangle=\int {d^{3}p\over (2\pi)^{3}}{1\over 2\omega_{p}}f(\vec{p}) \alpha^{\dagger}(\vec{p})|0\rangle, \end{eqnarray} while we write a $n$-particle state $|f\rangle\in\mathcal{H}_{1}^{\otimes\,n}$ as \begin{eqnarray} |f\rangle=\int \prod_{i=1}^{n}{d^{3}p_{i}\over (2\pi)^{3}} {1\over 2\omega_{p_{i}}}f(\vec{p}_{1},\ldots,\vec{p}_{n}) \alpha^{\dagger}(\vec{p}_{1})\ldots\alpha^{\dagger}(\vec{p}_{n})|0\rangle. \end{eqnarray}

For more on this, see the page about quantum field theory.

• A nice summary of the different quantization procedures can be found at page 4 and 5 in Klauber's Student friendly QFT.
• Also nice is http://www.scottaaronson.com/democritus/lec9.html

Abstract

There are many obstacles to make the process of quantization mathematical precise.

Already from first principles one encounters difficulties. Given that the classical description of a system is an approximation to its quantum description, obtained in a macroscopic limit (when $\hbar \to 0$), one expects that some information is lost in the limit. So quantization should somehow have to compensate for this. But how can a given quantization procedure select, from amongst the myriad of quantum theories all of which have the same classical limit, the physically correct one?Obstructions to Quantization by Mark J. Gotay

For this reason, many quantization schemes have been developed over the years which all have their individual shortcomings:

• Canonical quantization and its modern reformulation geometric quantization. Here we try to map the classical observables, which are functions in phase space, onto operators in a corresponding Hilbert space. The algebra of the observables in classical mechanics is given by the Poisson bracket, whereas the operators in Hilbert space obey the commutator algebra. (Both are instances of the Heisenberg algebra).
• Weyl quantization and its modern reformulation deformation quantization. Here we try to map the phase space formulation of classical mechanics (=Hamiltonian mechanics) onto the phase space formulation of quantum mechanics. This means that we map the Poisson bracket onto the Moyal bracket, which can be understood as a deformation of the Poisson bracket. In turn, the Moyal bracket becomes in the limit $\hbar \to 0$ the Poisson bracket.
• Path integral quantization.
• Group-theoretic approach to quantization, which is closely related to geometric quantization.
• Asymptotic quantization
• Stochastic quantization is based, roughly speaking, on the idea that the quantum indeterminacy is a result of a stochastic process.

• A nice summary can be found in Quantization Methods: A Guide for Physicists and Analysts by S. Twareque Ali, Miroslav Engliš.
• See also Obstructions to Quantization by Mark J. Gotay and Landsman, N.P.: Mathematical topics between classical and quantum mechanics. Springer Monographs in Mathematics. Springer-Verlag, New York, 1998.
• and the book Quantization of Gauge Systems by Henneaux and Teitelboim

Canonical Quantization

Whenever you have a classical phase space (symplectic manifold to mathematicians), functions on the phase space give an infinite dimensional Lie algebra, with Poisson bracket the Lie bracket. Dirac’s basic insight about quantization (“Poisson bracket goes to commutators”) was just that a quantum theory is supposed to be a unitary representation of this Lie algebra.

For a general symplectic manifold, how to produce such a representation is a complicated story (see the theory of “geometric quantization”). For a finite-dimensional linear phase space, the story is given in detail in the notes: it turns out that there’s only one interesting irreducible representation (Stone-von Neumann theorem), it’s determined by how you quantize linear functions, and you can’t extend it to functions beyond quadratic ones (Groenewold-van Hove no-go theorem). This is the basic story of canonical quantization.

For the infinite-dimensional linear phase spaces of quantum field theory, Stone-von Neumann is no longer true, and the fact that knowing the operator commutation relations no longer determines the state space is one source of the much greater complexity of QFT.

http://www.math.columbia.edu/~woit/wordpress/?p=7108

Canonical quantization is the original approach to quantization and goes back to Weyl, von Neumann, and Dirac

The procedure consists in assigning to the observables of classical mechanics (=real-valued functions $f(p,q)$ of $(p,q)=(p_1,\dots,p_n,q_1,\dots, q_n)\in\mathbb{R}^n\times\mathbb{R}^n$ (the phase space)), self-adjoint operators $Q_f$ on the Hilbert space $L^2(\mathbb{R}^n)$ in such a way that

• the correspondence $f\mapsto Q_f$ is linear;
• $Q_1=I$, where $1$ is the constant function, equal to one everywhere, and $I$ the identity operator;
• for any function $\phi:\mathbb{R}\to\mathbb{R}$ for which $Q_{\phi\circ f}$ and $\phi(Q_f)$ are well-defined, $Q_{\phi\circ f}=\phi(Q_f)$; and
• the operators $Q_{p_j}$ and $Q_{q_j}$ corresponding to the coordinate functions $p_j,q_j$ ($j=1,\dots,n$) are given by\begin{equation} Q_{q_j} \psi = q_j \psi, \qquad Q_{p_j} \psi =-\frac{ih}{2\pi} \,\frac{\partial \psi} {\partial q_j} \qquad \text{for } \psi \in L^2(\mathbb{R}^n,dq). \end{equation}

The Stone and von Neumann theorem then states that up to unitary equivalence, these operators are the unique operators acting on a Hilbert space $\mathcal H$, which satisfy an irreducibility condition.

• The standard reference is Dirac, P.A.M. [1967] The Principles of Quantum Mechanics. Revised Fourth Ed. (Oxford Univ. Press, Oxford).

Geometric Quantization

• For a short summary, see https://physics.stackexchange.com/questions/46015/why-quantum-mechanics/75775#75775
• For geometric quantization, great introductions are http://math.ucr.edu/home/baez//quantization.html and "Quantization is a mystery" by Ivan Todorov
• see also Geometric quantization; a crash course by Eugene Lerman
• Tuynman, G. What is prequantization, and what is geometric quantization?, in Proceedings, Seminar 1989 1990, Mathematical Structures in Field Theory is a very well-written introduction to the topic, and contains many references to further work.
• The standard textbook is "Geometric Quantization" by Woodhouse, see also the discussion about good literature on geometric quantization here.
• Higher prequantum geometry by Urs Schreiber
• Kirillov, A.A. [1990] Geometric quantization. In: Dynamical Systems IV: Symplectic Geometry and Its Applications. Arnol’d, V.I. and Novikov, S.P., Eds. Encyclopædia Math. Sci. IV. (Springer, New York) 137-172
• Souriau, J.-M. [1997] Structure of Dynamical Systems. (Birkhäuser, Boston).
• Woodhouse, N.M.J. [1992] Geometric quantization. Second Ed. (Clarendon Press, Oxford).

Weyl Quantization

• see Folland, G.B. [1989] Harmonic Analysis in Phase Space. Ann. Math. Ser. 122 (Princeton University Press, Princeton)

Deformation Quantization

These developments encourage attempts to view quantum mechanics as a theory of functions or distributions on phase space, with deformed products and brackets. We suggest that quantization be understood as a deformation of the structure of the algebra of classical observables, rather than as a radical change in the nature of the observables. Incidentally, the nontriviality of the deformations throws some light on the nontrivial Deformation theory and quantization I by Bayen, F., Flato, M., Fronsdal, C., Lichnerowicz, A., & Sternheimer, D. [1978]

• Deformations, stable theories and fundamental constants by R Vilela Mendes
• Deformation quantization: a survey by M Bordemann
• Bayen, F., Flato, M., Fronsdal, C., Lichnerowicz, A., & Sternheimer, D. [1978] Deformation theory and quantization I, II. Ann. Phys. 110, 61– 110, 111–151.
• Deformation Quantization in the Teaching of Quantum Mechanics by Allen C. Hirshfeld and Peter Henselder
• Deformation quantization in the teaching of Lie group representations by Alexander J. Balsomoa and Job A. Nable
• Rieffel, M.A. [1990] Deformation quantization and operator algebras. Proc. Sym. Pure Math. 45, 411–423.
• Rieffel, M.A. [1993] Quantization and C ∗ -algebras. In: C ∗ -Algebras: 1943- 1993, A Fifty Year Celebration. Doran, R.S., Ed. Contemp. Math. 167, 67–97.
• Rieffel, M.A. [1997] Questions on quantization. Preprint quant-ph/ 9712009.

Path Integral Quantization

see Path Integral Quantum Mechanics

Group-theoretic Approach to Quantization

In a previous paperl we have briefly outlined a method of quantization which follows closely the traditional method of geometric quantization of So uri au, Kostant, and others.2-4 The underlying rationale, however, is rather different: Instead of searching for quantizations of previously defined classical systems, the new approach tends to build directly, and without any ingredient other than a group law, the dynamical quantum systems. Thus, their quantum character is already determined by the symmetry group. The method is based on the close relation which exists among the spatial and dynamical properties of a system and its symmetry group, as well as of the slightly different character which the symmetry groups of classical and quantum systems present. Clearly, the difficulty of the procedure is the determination of the group for the case of interacting systems; in this respect, it fares no better than the conventional Kostant-Souriau (KS) theory. Nevertheless, our method may be applied directly in configuration space, thus avoiding the problem of characterizing the manifold of solutions5 of the classical system in order to quantize it. Quantization as a consequence of the symmetry group by Aldaya, V. & Azcarraga, J.A.

• Aldaya, V. & Azcarraga, J.A. [1982] Quantization as a consequence of the symmetry group: An approach to geometric quantization. J. Math. Phys. 23, 1297–1305.
• Isham, C.J. [1984] Topological and global aspects of quantum theory. In: Relativity, Groups, and Topology II. DeWitt, B.S. & Stora, R., Eds. (NorthHolland, Amsterdam) 1059–1290

Stochastic Quantization

see Review of stochastic mechanics by Edward Nelson

Quantization of Gauge Theories

• The standard book on the topic is Quantization of Gauge Systems by Marc Henneaux and Claudio Teitelboim

There are at least four extant approaches to quantization of gauge theories.

The first is gauge fixing: fix a gauge and quantize in that gauge. But when one tries to do this for Yang–Mills theories using the analogues of familiar gauge conditions (e.g. Lorentz gauge) the procedure may break down. The difficulty is explained by the fact that the gauge condition may fail to define a global transversal in the constraint surface, i.e. a hypersurface that meets each of the gauge orbits exactly once.

A second approach is reduced phase space quantization. Quotient out the gauge orbits to produce the reduced phase space. If this procedure goes smoothly (see section 10 below) the normal method of quantization can be applied to the resulting unconstrained Hamiltonian system. This approach faces the practical difficulty of having to solve the constraints, and even if one overcomes this difficulty one may find that the reduced phase space has features that complicate the quantization (see section 10 below).

The third approach is called Dirac constraint quantization. Here the procedure is to promote the first-class constraints to operators on a Hilbert space and then require that the vectors in the physical sector of this Hilbert space be annihilated by the constraint operators. Of course, the forming of the constraint operators is subject to operator ordering ambiguities. But even modulo such ambiguities, it can happen that the resulting Dirac quantization is inequivalent to that obtained by reduced phase space quantization. In such a case, which is the correct quantization? And how would one tell? I will return to these matters below.

The fourth approach is called BRST quantization after Becchi, Rouet, Stora, and Tyutin. The idea is to mirror the original gauge symmetry by a symmetry transformation on an extended phase space obtained by adding auxiliary variables. The additional phase space variables are chosen so that the BRST symmetry has a simple form that facilitates quantization.

http://pitt.edu/~jearman/Earman2003a.pdf

Quantization of Gravity

see also Quantum Gravity

What Quantization Scheme to Use? Well, in the 80 years people have pursued quantum gravity, they have tried every quantization scheme you could think of!

To get a sense of how complicated quantum gravity is (and an overview of the different approached), I recommend reading Rovelli's "Notes for a brief history of quantum gravity" arXiv:gr-qc/0006061, which is an easy read.

Just a few remarks about quantization schemes: quantization is always problematical on its own, in the sense that presumably nature is already quantum and formulating a procedure to go from classical to quantum is nonsensical. This is discussed in many articles, I'll give a few free good references, e.g., S Twareque Ali and Miroslav Engliš' "Quantization Methods: A Guide for Physicists and Analysts" (arXiv:math-ph/0405065) and MJ Gotay's " Obstructions to Quantization" (arXiv:math-ph/9809011).

http://physics.stackexchange.com/a/34410/37286

It is generally acknowledged that quantization is an ill-defined procedure which cannot be consistently applied to all classical systems.Obstructions to Quantization by Mark J. Gotay

Why is it interesting?

Quantization is what we call the difference between classical theories and quantum theories. A classical theory becomes a quantum theory through quantization.

Quantization is an art form which, when applied to classical physical theories, yields predictions of subatomic behavior which are in spectacular agreement with experiments. Ron Y. Donagi

Let me begin with a reminder that the quantum revolution did not erase our reliance on the earlier, classical physics. Indeed, when proposing a theory, we begin with classical concepts and construct models according to the rules of classical, pre-quantum physics. We know, however, such classical reasoning is not in accordance with quantum reality. Therefore, the classical model is reanalyzed by the rules of quantum physics, which comprise the true laws of Nature. This twostep procedure is called quantization.

The Unreasonable Effectiveness of Quantum Field Theory by R. Jackiw

FAQ

Is a third quantization possible?

see https://physics.stackexchange.com/questions/625/is-a-third-quantization-possible

Why there is no unique recipe for quantization of a classical theory?

see https://physics.stackexchange.com/questions/323937/why-there-is-no-unique-recipe-for-quantization-of-a-classical-theory

How can we understand the transition from quantum to classical physics?

For a nice discussion, see chapter 2 in Sleeping Beauties in Theoretical Physics by Thanu Padmanabhan:

"Particles do not follow trajectories. They are described by wavefunctions but under appropriate circumstances the constructive interference of the phases of the wavefunction will single out a path which we call a classical trajectory. The Hamilton-Jacobi Equation is just the lowest-order Schrodinger equation if we use the ansatz in Eq. (2.1). The ¨ mysterious procedure in Hamilton-Jacobi theory — of differentiating the solution to Hamilton-Jacobi equation and equating it to a constant — is just the condition for constructive interference of the phases of waves differing slightly in the parameter E. The procedure based on Hamilton-Jacobi theory works in classical mechanics because it is supported by the Schrodinger equation"

See also: Decoherence and the Transition from Quantum to Classical—Revisited by Zurek and The quantum-to-classical transition and decoherence by Maximilian Schlosshauer

What does quantization is not a functor really mean?

see https://​mathoverflow.net/​questions/​8606/​what-does-quantization-is-not-a-functor-really-mean

←-

Edit

History

“I went back to Cambridge at the beginning of October 1925, and resumed my previous style of life, intense thinking about these problems during the week and relaxing on Sunday, going for a long walk in the country alone. The main purpose of these long walks was to have a rest so that I would start refreshed on the following Monday. It was during one of the Sunday walks in October 1925, when I was thinking about this (uv- vu), in spite of my intention to relax, that I thought about Poisson brackets. I remembered something which I had read up previously, and from what I could remember, there seemed to be a close similarity between a Poisson bracket of two quantities and the commutator. The idea came in a flash, I suppose, and provided of course some excitement, and then came the reaction “No, this is probably wrong”. I did not remember very well the precise formula for a Poisson bracket, and only had some vague recollections. But there were exciting possibilities there, and I thought that I might be getting to some big idea. It was really a very disturbing situation, and it became imperative for me to brush up on my knowledge of Poisson brackets. Of course, I could not do that when I was right out in the countryside. I just had to hurry home and see what I could find about Poisson brackets. I looked through my lecture notes, the notes that I had taken at various lectures, and there was no reference there anywhere to Poisson brackets. The textbooks which I had at home were all too elementary to mention them. There was nothing I could do, because it was Sunday evening then and the libraries were all closed. I just had to wait impatiently through that night without knowing whether this idea was really any good or not, but I still think that my confidence gradually grew during the course of the night. The next morning I hurried along to one of the libraries as soon as it was open, and then I looked up Poisson brackets in Whitackers Analytical Dynamics, and I found that they were just what I needed.” Dirac

Criticism

In my opinion, canonical quantization looks like an algorithm to invert the classical limit of quantum theory, and not a fundamental principle.Quantum Theory as an Emergent Phenomenon: Foundations and Phenomenology by Stephen Adler

Now it doesn’t seem to be true that God created a classical universe on the first day and then quantized it on the second day. John Baez

Already from first principles one encounters difficulties. Given that the classical description of a system is an approximation to its quantum description, obtained in a macroscopic limit (when $\hbar \to 0$), one expects that some information is lost in the limit. So quantization should somehow have to compensate for this. But how can a given quantization procedure select, from amongst the myriad of quantum theories all of which have the same classical limit, the physically correct one?Obstructions to Quantization by Mark J. Gotay