User Tools

Site Tools

Trace: • Gauge Symmetry

Sidebar


Add a new page:

advanced_tools:gauge_symmetry

Gauge Symmetry

see also Gauge Models

Intuitive

A gauge symmetry is analogous to how we can describe something within one language through different words (synonyms). A description of the same thing in different languages is called a Duality.

When we describe things in physics, we have always some freedom in our description. For example, it doesn't matter what coordinate system we choose. It makes no difference where we choose the origin of the coordinate system or how it is oriented.

The computations can be different in different coordinate systems and usually, one picks a coordinate system where the computation is especially simple. However, the physics that we are describing, of course, doesn't care about how we describe it. It stays the same, no matter how we choose our coordinate system.

In modern physics, we no longer describe what is happening merely through the position of objects at a given time, as we do it in classical mechanics. Instead, we use abstract objects called fields. The best theory of what is happening in nature at the most fundamental level is quantum field theory. Like the electromagnetic field, these fields can get excited (think: we can produce a wave or ripple of the field). For example, when we excite the electron field we "produce" an electron.

The fields themselves are abstract mathematical entities that are introduced as convenient mathematical tools. With these new mathematical entities comes a new kind of freedom. Completely analogous to how we have the freedom to choose the orientation and the location of the origin of our coordinate system, we now have freedom in how we define our fields.

The freedom to "shift" or "rotate" our fields is called gauge symmetry. It is important to note that this symmetry is completely independent from the rotational and translational symmetry of our coordinate systems. When we "shift" or "rotate" a field we do not refer to anything in spacetime, but instead we "shift" and "rotate" merely our description of a given field.

A particular nice system to understand Yang-Mills theory in a non-technical context are financial markets.

Say, we represent different countries by different points on a lattice. Each country has its own currency. However, the absolute values of the different currencies has no meaning of all on the global money market. Instead, all that counts are the relationships between the different currencies. The exchange rates between different currencies is encoded in something we call connection.

Now, how can we make money on the money market?

Well, let's say we are a banker in London. We have a budget of 100 pounds. Our goal is to trade our currency against other currencies in such a way that we have in the end more than 100 pounds. This means, we need to look for profitable loops through the global money lattice. We are interested in loops, because to actually determine if have earned money, we need to compare our final amount of money with the 100 pounds we started with. This is only possible if the final amount of money is also given in pounds.

Let's say the exchange rates are as follows:

  • 1.5 dollars = 1 pound,
  • 1 dollar = 10 pesos,
  • 1 pound = 10 pesos.

How can we make money in this situation?

  1. We start by trading our 100 pound against 150 dollars.
  2. Then, we trade the 150 dollars against 1500 pesos.
  3. Finally we trade the 1500 pesos against 150 pounds.

Thus, by trading in a loop, we have gained 50 pounds.

The loops we considered here are exactly analogous to the Wilson loops used in quantum field theories. The gauge freedom corresponds here to the freedom to rescale the local currencies. For examples, England could introduce a new currency called "new-pound" and determine that 1 new-pound is worth 10 pounds. This wouldn't change the situation at the global money market at all because all banks would simply adjust their exchange rates:

  • 0.15 dollars = 1 new-pound,
  • 1 dollar = 10 pesos,
  • 1 new-pound = 1 pesos.

Absolute value has no meaning and this is what we call gauge freedom. We can't make more money simply because we change the local value of our currency.

The thing we used in the situation above to earn money is called arbitrage. An arbitrage means a possibility to earn money without any risk. The arbitrage possibilities are completely encoded in closed loops.

In physics, we usually don't use Wilson loops, but instead, work with gauge field strengths (think electric or magnetic field strength). These gauge field strengths $F_{\mu\nu}$ correspond to infinitesimal Wilson loops around a given point $x$.

Another Analogy due to Lawrence Krauss

So, imagine the universe as a big chessboard. I could change every white square on a chessboard to a black square and every black square to a white square and the game would be exactly the same. That’s the simple kind of symmetry. Now I can turn it into a gauge symmetry by making it much trickier. I can say, “Let me just change locally, whenever I want, a white square to a black square or a black square to a white square. Not everywhere but place to place." Now the chessboard doesn’t look the same at all, so the game can’t be the same unless I also have a rule book—a coordinate system for what happens at every point—containing rules for the pieces of the chessboard to follow to keep the game the same, rules that account for everywhere I have changed the color of a square. That becomes a very weird symmetry.

As I explain in the book, this sort of symmetry tells you how to go from the conservation of charge to the theory of electromagnetism. It says, “I could change the sign of each electric charge in nature locally. But I have to have a rule book.” What's the rule book? In this case, it’s the electromagnetic field. Even though gauge symmetry is something that most people find obscure, it’s the most visible thing in the world—and if you don’t have it, things fall apart in surprising ways. Whenever you look at a lightbulb, you're able to see light because nature has this weird symmetry. https://www.scientificamerican.com/article/q-a-lawrence-krauss-on-the-greatest-story-ever-told/

Gauge Symmetry in Electrodynamics

Fields in physics are something which associate with each point in space and with each instance in time a quantity. In case of electromagnetism this is a quantity describing the electric and magnetic properties at this point. Each of these two properties turn out to have a strength and a direction. Thus the electric and magnetic fields associate with each point in space and time an electric and a magnetic magnitude and a direction. For a magnetic field this is well known from daily experience. Go around with a compass. As you move, the magnetic needle will arrange itself in response to the geomagnetic field. Thus, this demonstrates that there is a direction involved with magnetism. That there is also a strength involved you can see when moving two magnets closer and closer together. How much they pull at each other depends on where they are relative to each other. Thus there is also a magnitude associated with each point. The same actually applies to electric fields, but this is not as directly testable with common elements. Ok, so it is now clear that electric and magnetic fields have a direction and a magnitude. Thus, at each point in space and time six numbers are needed to describe them: two magnitudes and two angles each to determine a direction.

When in the 19th century people tried to understand how electromagnetism works they also figured this out. However, they made also another intriguing discovery. When writing down the laws which govern electromagnetism, it turns out that electric and magnetic fields are intimately linked, and that they are just two sides of the same coin. That is the reason to call it electromagnetism.

In the early 20th century it then became clear that both phenomena can be associated with a single particle, the photon. But then it was found that to characterize a photon only two numbers at each point in space and time are necessary. This implies that between the six numbers characterizing electric and magnetic fields relations exist. These are known as Maxwell equations in classical physics, or as quantum Maxwell dynamics in the quantum theory. If you would add, e. g., electrons to this theory, you would end up with quantum electro dynamics - QED.

So, this appeared as a big step forward in describing numerically electromagnetism. However, when looking deeper into the mathematical concepts, it turned out to be technically rather complicated to describe all electric and magnetic phenomena with just these two properties of the photon. It was then that people noticed that including a certain redundancy things became much simpler. An ideal solution was found to describe electromagnetism with four numbers at each space-time point, instead of two. These can then not be independent, of course. And it is here where the symmetry comes into play: It is a symmetry concept which connects these numbers.

First, here is a simple example of how it works. Take someone walking only along the circumference of a circle. Then you can either describe her position by the height and width from the center of the circle. Or you can use the angle around the circle's circumference. Both is equally valid. Hence, the two numbers of the first choice are uniquely connected to the second choice: Changing the angle will change both height and width simultaneously! And because this connection comes from the fact that the circle is rotationally symmetric, it is this symmetry. And the symmetry of a circle is called U(1). Now, the relation between the four convenient numbers and the two important ones is quite in analogy to this case, and is therefore also a U(1) symmetry. That is how the symmetry becomes associated with electromagnetism. This tells us that if we change the four numbers by, so to say, moving them around on the circle, we do not change the two numbers describing the photon (or the six describing the electric and magnetic field). Only when we move away from the circumference, the two (and six) numbers change. In this way the symmetry is only helping us in a mathematical description, but is not influencing what we can measure. It is therefore also called a gauge symmetry. http://axelmaas.blogspot.de/2010/10/electromagnetism-photons-and-symmetry.html

Recommended Resources:

See also

Concrete

Gauge Transformations in Electrodynamics

The Lagrangian of electrodynamics reads

$$ \mathcal{L}_{EM} = -{1\over 4} F_{\mu \nu}F^{\mu \nu} - J^{\mu}A_{\mu} $$ where $F^{\mu \nu} \equiv \partial^{\mu}A^{\nu} - \partial^{\nu}A^{\mu} $

The crucial observation is now that $A^{\mu}$ does not uniquely specify the action. Instead, we can take an arbitrary function $\chi(x^{\mu})$, and the action will be unchanged under the transformation \begin{eqnarray} A^{\mu} \rightarrow A'^{\mu} = A^{\mu} + \partial^{\mu}\chi . \end{eqnarray} To see this explictly we first calculate \begin{eqnarray} F'^{\mu \nu} &=& \partial^{\mu}A'^{\nu} - \partial^{\nu}A'^{\mu} = \partial^{\mu}(A^{\nu}+\partial^{\nu}\chi) - \partial^{\nu}(A^{\mu}+ \partial^{\mu}\chi) \\ &=& \partial^{\mu}A^{\nu} - \partial^{\nu}A^{\mu} + \partial^{\mu} \partial^{\nu}\chi -\partial^{\mu}\partial^{\nu}\chi \\ &=& F^{\mu \nu} \label{eq:invarianceoffmn} \end{eqnarray} So the field strength tensor $ F^{\mu \nu}$ is indeed unchanged by this transformation: $F'^{\mu \nu} = F^{\mu \nu}$.

In addition we can calculate that $J^{\mu}A_{\mu} \rightarrow J^{\mu}A_{\mu} + J^{\mu}\partial_{\mu}\chi$. To see this, we integrate the second term by parts with the usual boundary conditions, \begin{eqnarray} \int d^4x J^{\mu}\partial_{\mu}\chi = -\int d^4x (\partial_{\mu}J^{\mu})\chi \end{eqnarray} Now we use that according to Maxwell's equations, $\partial_{\mu}J^{\mu} = \partial_{\mu}\partial_{\nu}F^{\mu \nu} \equiv 0$ because $F^{\mu \nu}$ is totally antisymmetric.

Therefore, both $F^{\mu \nu}$ and $J^{\mu}\partial_{\mu}\chi$ are invariant under the transformation

\begin{eqnarray} A^{\mu} \rightarrow A'^{\mu} = A^{\mu} + \partial^{\mu}\chi , \end{eqnarray}

which is called a gauge transformation. This means immediately that the action is unchanged and that this transformation is a symmetry of the system.

Local Transformations

Abstract

The group of gauge transformations $G$ means the bundles automorphisms which preserve the Lagrangian. (Source)

The gauge group is simply one fiber of the bundle, i.e. for example, $SU(2)$.

We denote the space of all connections by $A$. Now, to get physically sensible results we must be careful with these different notions:

Integration should therefore be carried out on the quotient space $\mathcal{G}=A/G$. Now $A$ is a linear space but $\mathcal{G}$ is only a manifold and has to be treated with more respect. Thus for integration purposes a Jacobian term arises which, in perturbation theory, gives rise to the well-known Faddeev-Popov "ghost" particles. Nonperturbatively it seems reasonable that global topological features of $\mathcal{G}$ will be relevant.

Geometrical Aspects of Gauge Theories by M. F. Atiyah

There are different "high-level" descriptions of gauge theories. The most famous one makes use of the fibre bundle formalism. Another possibility is the "loop formulation".

Gauge potentials take their values in the Lie algebra $\mathfrak{g}$ of the gauge group $\mathcal G$.

It is important to note that there is the difference between a group $G$ and the corresponding gauge group $\mathcal G$.

$G$ is simply a set of symmetry transformations. In contrast, $\mathcal G$ is a group of smooth functions on spacetime that take values in $G$. More mathematically, the group of gauge transformations $ \mathcal G$ means the bundles automorphisms which preserve the Lagrangian. (Source). The group $G$ is simply one fibre of the bundle, i.e. for example, $SU(2)$.

Moreover, one can argue that the "true" gauge symmetry is given by a subset of $\mathcal G$ called $\mathcal G_\star$:

\begin{align} \mathcal{G}_\star &= \big \{ \text{ set of all } g(x) \text{ such that } g \to 1 \text{ as } |x| \to \infty \big \} \notag \\ \mathcal{G} &= \big \{ \text{ set of all } g(x) \text{ such that } g \to \text{ constant element of $G$, not necessarily $1$ as } |x| \to \infty \big \} \end{align}

This comes about when one considers Gauss law to identify physical states. Such physical states are invariant under $\mathcal{G}_\star$ and thus this subgroup connects physically redundant variables in the theory.

Since the elements of $\mathcal G$ go only to a constant, which is not necessarily $1$ at spatial infinity, we have

\begin{align} \mathcal{G} / \mathcal{G}_\star \sim \text{ set of constant g's } \sim G \notag \\ \mathcal{G} / \mathcal{G}_\star \sim G \text{ is the Noether symmetry of the theory defined by the charges} \end{align}

All transformations $g(x)$ which go to a constant at spatial infinity that is not $1$ act as a Noether symmetry of the theory.

For more on this see, section 10.3 and chapter 16 in Quantum Field Theory - A Modern Perspective by V. P. Nair.

We denote the space of all connections by $\mathcal A$ (= the space of all gauge potentials $A_i$). This space is a an affine space, which simply means that any potential $A_i$ can be written as $A_i^{(0)} + h_i$, where $A_i^{(0)}$ is a given fixed potential and $h_i$ is an arbitrary vector field that takes values in the Lie algebra. Geometrically this means that, any two points in $\mathcal A$ can be connected by a straight line.

For two potentials $A_i^{(1)}$ and $A_i^{(2)}$, we can define the following sequence of gauge potential configurations

$$ A_i(x,\tau) = A_i^{(1)}(1-\tau) + \tau A_i^{(2)} ,$$

where $0 \leq \tau \geq 1$ parametrizes the straight line between the two configurations. (Topologically this space is rather trivial).

The configuration space of the theory is $\mathcal C = \mathcal A / \mathcal G_\star$.

Now, to get physically sensible results we must be careful with these different notions:

Integration should therefore be carried out on the quotient space $G=\mathcal A/\mathcal{G}_\star$. Now $\mathcal A$ is a linear space but $\mathcal{G}_\star$ is only a manifold and has to be treated with more respect. Thus for integration purposes a Jacobian term arises which, in perturbation theory, gives rise to the well-known Faddeev-Popov "ghost" particles. Nonperturbatively it seems reasonable that global topological features of $\mathcal{G}_\star$ will be relevant.

Geometrical Aspects of Gauge Theories by M. F. Atiyah

Gauge symmetry sometimes appears to be a curious shell game. One starts with some initial global symmetry algebra and makes it “local” via the introduction of new degrees of freedom, enlarging the symmetry algebra enormously; then, states that differ by gauge transformations are identified as the same physical state, effectively reducing the symmetry algebra. It is typically expected that the reduced symmetry algebra relating physical observables is the same as the initial algebra. In which case, the net effect of the gauge procedure, is to introduce new dynamical degrees of freedom (the gauge bosons). In the end, the advantage of the redundant description over a description involving only physical degrees is that the physical description is nonlocal. […] It has long been known that for gravity in asymptotically flat space [1, 2] or asymptotically AdS3 [3], the final physical symmetry algebra is an infinite-dimensional enhancement of the “global part” of the gauge group. Only recently, however, has it been realized that the enhancement also occurs for higher dimensional gravity, Maxwell theory, Yang–Mills theory, and string theory, and moreover, that the symmetry constrains the IR structure via nontrivial Ward identities [4–15].https://arxiv.org/abs/1510.07038

Why is it interesting?

Gauge symmetries are at the heart of the best theory of fundamental interactions, the standard model of particle physics. Theories that make use of gauge symmetry are commonly called gauge theories.

In addition to this application, gauge symmetry can also be useful to understand finance. This is shown, for example, in

Gauge symmetry principles are regularly invoked in the context of justification, as deep physical principles, fundamental starting points in thinking about why physical theories are the way they are, so to speak.

“On continuous symmetries and the foundations of modern physics” by CHRISTOPHER A. MARTIN

Symmetry dictates interaction

Cheng-Ning Yang

We do not yet have a full picture of how nature overcomes the dichotomy between simple fundamental laws and complex emergent phenomena. But particle physics has made huge progress in this direction and the key words are gauge theory. Gauge theory is the essential concept out of which the Standard Model is built: a concept that has all the features of a fundamental principle of nature. It is elegant (based on symmetry considerations), robust (no continuous deformations of the theory are generally allowed), and predictive (given the field content, all processes are described by a single coupling constant). In short, it has all the requirements for a physicist to see simplicity in it. The magic about gauge theory lies in the richness of its structure and its ability to produce, out of a simple conceptual principle, a great variety of different manifestations. Long-range forces, short-range forces, confinement, dynamical symmetry breaking are all phenomena described by the same principle. The vacuum structure of gauge theory is unbe- lievably rich, with θ-vacua, instantons, chiral and gluon condensates, all being expressions of the same theory. The phase diagram at finite temperature and density exhibits a variety of new phenomena and states of matter. In short, gauge theory is an exquisite tool to make complexity out of simplicity.

https://arxiv.org/pdf/1710.07663.pdf

FAQ

What's the interpretation of gauge symmetry?
The best summary can be found starting at page 7 in http://philsci-archive.pitt.edu/223/1/Objectivity.pdf

Especially: "local gauge invariance in quantum theory does not imply the existence of an external electromagnetic field"!

Do we really care about the gauge group or only about the corresponding Lie algebra?
Oftentimes, the notion "gauge group" is used a bit sloppy. Perturbative effects only depend on the local structure of the group and hence only on the Lie algebra. There are many groups with the same Lie algebra and in many situations it is not clear which group is the "correct" group that describes the physics. From experiments, we only learn something about the Lie algebra. (This is, for example, mentioned in Physics and Geometry by EDWARD WITTEN).

For example, there are thirteen groups with the same Lie algebra as the famous $SU(3) \times SU(2) \times U(1)$ gauge symmetry of the standard model. In addition, there are good reasons to believe that the correct gauge group of the standard model is not $SU(3) \times SU(2) \times U(1)$ , but rather $S(U(3) \times U(2) )$.

Is it possible to derive gauge symmetry from something else?
Yes:

Gauge Symmetry from Lorentz Symmetry

This is done, for example, in Vol. 1 of Weinberg's Quantum Field Theory book in section 5.9.

Weinberg shows that a massless spin 1 vector field $A_\mu$ cannot be a four-vector under Lorentz transformations. Instead, he derives that under a Lorentz transformation $\Lambda$ a massless spin 1 vector field $A_\mu$ transforms as follows:

$$ U(\Lambda) A_\mu(x) U^{-1}(\Lambda) = \Lambda^\nu_\mu A_\nu(\Lambda x) + \partial_\mu \Omega(x,\Lambda), $$

where $\Omega(x,\Lambda)$ is some function of the creation and annihilation operators. Therefore, he concludes that in order to get a Lorentz invariant theory it is not enough to write down terms in the Lagrangian that are invariant under the "naive" transformation $A_\mu \to \Lambda^\nu_\mu A_\nu$, but additionally the terms must be invariant under $A_\mu \to A_\mu + \partial_\mu \Omega $. This second part of the transformation is the well known gauge transformation of $A_\mu$. In this sense, the gauge symmetry follows from the Lorentz symmetry.

A summary of Weinberg's argument with an easier notation can be found in this article.

This emergence of gauge symmetry was also discussed nicely from a bit different perspective in this recent paper by Nima Arkani-Hamed, Laurentiu Rodina, Jaroslav Trnka.

“Maxwell’s theory and Einstein’s theory are essentially the unique Lorentz invariant theories of massless particles with spin $j =1$ and $j =2$”.

Photons and Gravitons in Perturbation Theory: Derivation of Maxwell's and Einstein's Equations by Steven Weinberg

Take note that there is a close connection between this kind of argument and the famous Weinberg-Witten Theorem.

Gauge Symmetry from Asymptotic Freedom

This point of view is formulated by Wilczek in his article "What QCD tells us about nature - and why we should listen":

Summarizing the argument, only those relativistic field theories which are asymptotically free can be argued in a straightforward way to exist. And the only asymptotically free theories in four space-time dimensions involve nonabelian gauge symmetry, with highly restricted matter content. So the axioms of gauge symmetry and renormalizability are, in a sense, gratuitous. They are implicit in the mere existence of non-trivial interacting quantum field theories.

What QCD tells us about nature - and why we should listen by F. Wilczek

Does gauge symmetry really "dictate interaction"?
Definitely not alone.

This modification is not uniquely dictated by the demand of local gauge invariance. There are infinitely many other gauge-invariant terms that might be added to the Lagrangian if gauge invariance were the only input to the argument. In order to pick out the minimal modification uniquely, we must bring in, besides gauge invariance and knowledge of field theories generally, the requirements of Lorentz invariance, simplicity, and, importantly, renormalizability. (For example, a Pauli term is Lorentz invariant and gauge invariant but not renormalizable.) The minimal modification is then the simplest, renormalizable, Lorentz and gauge-invariant Lagrangian yielding second-order equations of motion for the coupled system (O’Raifeartaigh, 1979). The point is simply that, in the context of the gauge argument, the requirement of local gauge invariance gets a lot of its formal muscle in combination with other important considerations and requirements.

“On continuous symmetries and the foundations of modern physics” by CHRISTOPHER A. MARTIN

The Pauli Term is $\frac{m_0}{\Lambda_0^2}\bar\Psi \gamma^{\mu \nu} F_{\mu \nu} \Psi$, where $\gamma^{\mu \nu}$ is $[\gamma^\mu,\gamma^\nu]$. It is non-renormalizable, because the factors coming from $\frac{m_0}{\Lambda_0^2}$ in higher order of perturbation theory, have to be compensated by more and more divergent integrals.

Moreover, any theory can be made gauge invariant by the "Stueckelberg trick":

While many older textbooks rhapsodize about the beauty of gauge symmetry, and wax eloquent on how “it fully determines interactions from symmetry principles”, from a modern point of view gauge invariance can also be thought of as by itself an empty statement. Indeed any theory can be made gauge invariant by the “Stuckelberg trick”–elevating gauge transformation parameters to fields–with the “special” gauge invariant theories distinguished only by realizing the gauge symmetry with the fewest number of degrees of freedom.

https://arxiv.org/pdf/1612.02797.pdf

This is similar to the discussion about the role of "general covariance" in general relativity. According to Einstein, "general covariance" is the symmetry principle at the heart of general relativity. However, it was quickly noted by Kretschmann that any theory can be formulated in a general covariant way.

What are alternatives to the gauge paradigm?
See, for example, spin-helicity formalism and the references there.

Loop Formulation:

See Anandan (1983) who argues that from both the physical and mathematical points of view, the holonomy contains all the relevant (gauge-invariant) information. Specifically, the connection can be constructed (up to gauge transformation) from a knowledge of the holonomies. Formalizing gauge theories in terms of holonomies associated with (non-local) loops in space appears, though, to require a revamped conception of the notion of a physical field (see Belot, 1998).

“On continuous symmetries and the foundations of modern physics” by CHRISTOPHER A. MARTIN

For more on the loop space formulation of quantum field theory, have a look at the small book "Some Elementary Gauge Theory Concepts" by Sheung Tsun Tsou, Hong-Mo Chan

Constrained Hamiltonian Formalism

See, for example, "Tracking down gauge: an ode to the constrained Hamiltonian formalism" by JOHN EARMAN

Where does gauge symmetry come from?

What Nielsen imagines is that the whole cosmos is just at the point of a phase transition between two phases. He and his colleagues, such as Don Bennett, try to demonstrate that many of the observed properties of the elementary particles arise simply from this fact, independently of whatever the fundamental laws of physics are. They want to say that, just as bubbles are universally found in liquids that are boiling, the fundamental particles we observe may be simply universal consequences of the universe being balanced at the point of a transition between phases. If so, their properties may to a large extent be independent of whatever fundamental law governs the world.

[…]

In fact, Nielsen and his colleagues do claim some successes for the hypothesis of random fundamental dynamics. Among them is the fact that all the fundamental interactions must be gauge interactions, of the type described by Yang-Mills theory and general relativity. This means that the world would appear at large scales to be governed by these interactions, whether or not they are part of the fundamental description of the world at the Planck scale. This last claim is, in fact, rather well accepted among particle theorists. It has been independently confirmed by Steven Shenker and others.

The Life of the Cosmos by Lee Smolin

Such a point of view is supported, for example, by observations in condensed matter physics:

Well, all the asymptotic behavior and renormalization group fixed points that we look at in condensed matter theory seem to grow symmetries not necessarily reflecting those of the basic, underlying theory. In particular, I will show some experiments tomorrow, where, in fact, one knows for certain that the observed symmetry grows from a totally unsymmetric underlying physics. Although as a research strategy I think what you say about postulating symmetry is totally unarguable, one can remark, in opposition, that it is only the desperate man who seeks after symmetry! If we truly understand a theory, we should see symmetry coming out or, on the other hand, failing to appear. So I am certainly not criticizing you on strategy. But you recognize - you put it very nicely, and I was relieved to hear it - that the renormalization group principle works in a large space, there are many fixed points, and there are many model field theories. So I am still unclear as to the origin of your faith that string theory should give us the standard model rather than some other type of local universe.

Michael Fisher in Conceptual Foundations of Quantum Field Theory, Edited by Cao

Why do we need gauge symmetry?

Is gauge symmetry an autonomous concept, logically independent of other leading principles of physics? On the contrary, it appears to be mandatory, in the theory of vector particles, to insure consistency with special relativity and quantum mechanics. For if the transverse parts of the vector field produce excitations that have a normal probabilistic interpretation (i.e., the square of their amplitude is the probability for their presence), then Lorentz invariance implies that the longitudinal parts produce excitations that are, in the jargon of quantum theory, ghosts. That is to say, the square of their amplitudes is minus the probability for their presence, so that when we contemplate their production we are confronted with the specter of negative probabilities, which on the face of it are senseless. Gauge invariance saves the day by insuring that the longitudinal modes decouple, i.e. that transition amplitudes to excite such modes actually vanish. Thus gauge invariance is required, in order to insure that no physical process is assigned a negative probability. Yang-Mills Theory In, Beyond, and Behind Observed Reality by Frank Wilczek

See also: https://www.physicsforums.com/threads/any-good-idea-how-non-abelian-gauge-symmetries-emerge.927901/

So what does this mean? What’s the point of having a local symmetry if we can just choose a gauge (in fact, we have to choose a gauge to do any computations) and the physics is the same? There are two answers to this question. First, it is fair to say that gauge symmetries are a total fake. They are just redundancies of description and really do have no physically observable consequences. In contrast, global symmetries are real features of nature with observable consequences. For example, global symmetries imply the existence of conserved charges, which we can test. So the first answer is that we technically don’t need gauge symmetries at all. The second answer is that local symmetries make it much easier to do computations. You might wonder why we even bother introducing this field Aµ which has this huge redundancy to it. Instead, why not just quantize the electric and magnetic fields, that is Fµν, itself? Well you could do that, but it turns out to be more of a pain than using Aµ. To see that, first note that Fµν as a field does not propagate with the Lagrangian L = − 1 4 Fµν 2 . All the dynamics will be moved to the interactions. Moreover, if we include interactions, either with a simple current AµJµ or with a scalar field φ ⋆Aµ∂µφ or with a fermion ψ¯γµAµψ, we see that they naturally involve Aµ. If we want to write these in terms of Fµν we have to solve for Aµ in terms of Fµν and we will get some crazy non-local thing like Aν = ∂ν Fµν. Then we’d have to spend all our time showing that the theory is actually local and causal. It turns out to be much easier to deal with a little redundancy so that we don’t have to check locality all the time. Another reason is that all of the physics of the electromagnetic field is not entirely contained in Fµν. In fact there are global properties of Aµ that are not contained in Fµν but that can be measured. This is the Aharanov-Bohm effect, that you might remember from quantum mechanics. Thus we are going to accept that using the field Aµ instead of Fµν is a necessary complication. So there’s no physics in gauge invariance but it makes it a lot easier to do field theory. The physical content is what we saw in the previous section with the Lorentz transformation properties of spin 1 fields.

http://isites.harvard.edu/fs/docs/icb.topic473482.files/08-gaugeinvariance.pdf

We might instead give a gauge-invariant interpretation, taking the physical state as specified completely by the gauge-invariant electric and magnetic field strengths. In this case, electromagnetism is deterministic since the gauge invariance that threatened determinism is in effect washed away from the beginning. However, in the case of non-trivial spatial topologies, the gauge-invariant interpretation runs into potential complications. The issue is that in this case there are other gauge invariants. So-called holonomies (or their traces, Wilson loops) – the line integral of the gauge potential around closed loops in space – encode physically significant information about the global features of the gauge field. The problem is that these gauge invariants, being ascribed to loops in space, are apparently non-local. But, coming full circle, providing a local description requires appeal to non-gauge-invariant entities such as the electromagnetic potential, whose very reality is in question according to the received understanding. The context for this discussion is the interpretation of the well-known Aharonov–Bohm (A–B) effect

“On continuous symmetries and the foundations of modern physics” by CHRISTOPHER A. MARTIN

Why do we localize the global symmetry?

Since $\Lambda$ is a constant, however, this gauge transformation must be the same at all points in space-time; it is a global gauge transformation. So when we perform a rotation in the internal space of $\phi$ at one point, through an angle $\Lambda$, we must perform the same rotation at all other points at the same time. If we take this physical interpretation seriously, we see that it is impossible to fulfil, since it contradicts the letter and spirit of relativity, according to which there must be a minimum time delay equal to the time of light travel. To get round this problem we simply abandon the requirement that $\Lambda$ is a constant, and write it as an arbitrary function of space-time, $\Lambda(x^\mu)$. This is called a local gauge transformation, since it clearly differs from point to point.

page 93 in Quantum Field Theory by Ryder

See also https://www.nikhef.nl/~t45/ftip/Ch11.pdf and http://www-personal.umich.edu/~jbourj/peskin/group%20project.pdf

First, the initial and all-important demand of local as opposed to global gauge invariance is anything but self-evident, and presumably it must be argued for on some basis. Historically, the arguments surrounding the ‘demand’ as such are quite thin. The most prevalent form goes back to Yang and Mills’ remarks to the effect that ‘local’ symmetries are more in line with the idea of ‘local’ field theories. Arguments from a sort of locality, and especially those predicated specifically on the demands of STR (i.e. no communication-at-a-distance) (See for example Ryder (1996, p. 93)). , are somewhat suspect, however, and careful treading is needed. Most immediately, the requirement of locality in the STR sense – say, as given by the lightcone structure – does not map cleanly onto to the global/local distinction figuring into the gauge argument – i.e. $G_r$ vs. $G_{\infty r}$ . Overall, the question of how ‘natural’, physically, this demand is, is not uncontentious. This is especially so in light of the received view of gauge transformations which maintains that they have no physical significance or counterpart (more below). I will return briefly in the next section to considering possible

“On continuous symmetries and the foundations of modern physics” by CHRISTOPHER A. MARTIN

What conserved quantities follow from gauge symmetries?
Using Noether's first theorem we find that the conserved charges that would follow from invariance under gauge transformations are identically zero. This is shown, for example, in section 3.4.1 here.

However, using Noether's second theorem we can derive relations between our equations of motion, that are known as Bianchi identities.

Is a gauge symmetry really a symmetry?
No!

gauge symmetries aren’t real symmetries: they are merely redundancies in our description of the system.David Tong

[Gauge symmetry], thinking about it as a symmetry is a bad idea, thinking about it as being broken is a bad idea.

Duality and emergent gauge symmetry - Nathan Seiberg

The problem with gauge symmetry is that it is not a symmetry in the sense of quantum mechanics. A symmetry is the invariance of the Hamiltonian under transformations of quantum states, which are elements of a Hilbert space. Gauge symmetry is not a symmetry because the corresponding transformation does not change the quantum states. Gauge symmetry acts trivially on the Hilbert space and does not relate physically distinct states. A gauge transformation is like a book by James Joyce: it seems that something is going on, but nothing really happens. Gauge symmetry is the statement that certain degrees of freedom do not exist in the theory. This is why gauge symmetry corresponds only to as a redundancy of the theory description. The non-symmetry nature of gauge symmetry explains why gauge symmetry, unlike global symmetry, cannot be broken by adding local operators to the action: gauge symmetry is exact at all scales. The only way to “break” gauge symmetry is adding to the theory the missing degrees of freedom, but this operation is not simply a deformation of the theory (as the case of adding local operators to an action with global symmetry) but corresponds to considering an altogether different theory. The non-symmetry nature of gauge symmetry also explains trivially the physical content of the Higgs theorem. For a spontaneously-broken global symmetry, an infinite number of vacuum states are related by the symmetry transformation. This leads to the massless modes dictated by the Goldstone theorem. In a spontaneously-broken gauge symmetry, there is a single physical vacuum and thus there are no massless Goldstones. Gauge symmetry does not provide an exception to the Goldstone theorem, simply because there is no symmetry to start with. For gauge symmetry, the word ‘symmetry’ is a misnomer, much as ‘broken’ is a misnomer for spontaneously broken symmetry. But as long as the physical meaning is clear, any terminology is acceptable in human language. The important aspect is that the mathematical language of gauge symmetry (both in the linear and non-linear versions) is extremely pow- erful in physics and permeates the Standard Model, general relativity, and many systems in condensed matter. As the redundancy of degrees of freedom is mathematically described by the same group theory used for quantum symmetries, the use of the word ‘symmetry’ seems particularly forgivable. Does this necessarily make gauge symmetry a fundamental element in the UV? The property of gauge symmetry of being – by construction – valid at all energy scales may naively suggest that gauge symmetry must be an ingredient of any UV theory from which the Standard Model and general relativity are derived. On the contrary, many examples have been constructed – from duality to condensed-matter systems – where gauge symmetry is not fundamental, but only an emergent property of the effective theory [41]. Gauge symmetry could emerge in the IR, without being present in the UV theory. If this is the case, gauge symmetry is not the key that will unlock the mysteries of nature at the most fundamental level. The concept of symmetry has given much to particle physics, but it could be that it is running out of fuel and that, in the post-naturalness era, new concepts will replace symmetry as guiding principles.

https://arxiv.org/pdf/1710.07663.pdf#page23

See https://youtu.be/XM4rsPnlZyg?t=18m38s

But there are several reasons not to accept this view. First of all terminology. When we say gauge symmetry, this is really a misnomer. It's a misnomer because in physics gauge symmetry is not a symmetry. It is not a symmetry of anything. Symmetry is a set of transformations that act on physical observables. They act on the Hilbert space. The Hilbert space is always gauge invariant. So the gauge symmetry doesn't even act on the Hilbert space. So it's not a symmetry of anything. […] Second, gauge symmetry can be made to look trivial. So, I'll give one trivial example and then I'll make it more elaborate… [explains the Stückelberg mechanism, where one introduces a Stückelberg field to make a non U(1) gauge invariant Lagrangian, gauge invariant] This is almost like a fake… This gauge symmetry is what we would call emergent, except that in this case it is completely trivial. The second thing which is wrong about gauge symmetry, which suggests that it's not fundamental is that, it started in condensed matter physics, people talked about spontaneous symmetry breaking. That was crucial in the context of superconductivity and superfluidity and so forth. And the recent Nobel price in physics was also associated with spontaneous gauge symmetry breaking. That of Higgs, and Englert. This is all very nice and physicists love to talk about spontaneous symmetry breaking, but this is a bit too naive. First of all I've already emphasized that a gauge symmetry is not a symmetry. And since it is not a symmetry, how could it possibly be broken. You can break a symmetry that exists, but you cannot break a symmetry that does not exist. Second, the phenomenon of spontaneous symmetry breaking is often associated with the fact that the system goes to infinity. Concretely in quantum mechanics, you never have symmetry breaking. It is only in quantum field theory or statistical mechanics, where we have volume going to infinity we have an infinite number of degrees of freedom and there we have this phenomenon of spontaneous symmetry breaking. That's not true for gauge theories. For gauge theories, we have a lot of symmetry. At every point of space we have a separate symmetry. But the number of degrees of freedom that transform under a given symmetry transformation is always finite. Nothing goes off to infinity. So the gauge symmetry cannot be spontaneously broken. The ground state is always unique. Or if you wish, all these would-be separate ground states are all related to each other by a gauge transformation. […] I said that gauge symmetry cannot be ultimate symmetry because it's so big, there is a separate transformation at every point in space. So the breaking of a gauge theory cannot happen, I can use a phrase from the financial crisis in 2008 that a gauge symmetry is so big, it's too big to fail.

Duality and emergent gauge symmetry - Nathan Seiberg

See also Seiberg's slides starting at page 30 here http://research.ipmu.jp/seminar/sysimg/seminar/1607.pdf:

Gauge symmetry is deep

•Largest symmetry (a group for each point in spacetime)

•Useful in making the theory manifestly Lorentz invariant, unitary and local (and hence causal)

But

•Because of Gauss law the Hilbert space is gauge invariant.( More precisely, it is invariant under small gauge transformation; large gauge transformations are central.)

•Hence:gauge symmetry is not asymmetry.

• It does not act on anything.

• A better phrase is gauge redundancy.

Gauge symmetries cannot break

•Not a symmetry and hence cannot break

•For spontaneous symmetry breaking we need an infinite number of degrees of freedom transforming under the symmetry. Not here.

•This is the deep reason there is no massless Nambu-Goldstone boson when gauge symmetries are “broken.”

Gauge symmetries cannot break For weakly coupled systems (e.g. Landau-Ginsburg theory of superconductivity, or the weak interactions) the language of spontaneous gauge symmetry breaking is appropriate and extremely useful[Stueckelberg,Anderson,Brout, Englert,Higgs].

Global symmetries can emerge as accidental symmetries at long distance. Then they are approximate. Exact gauge symmetries can be emergent.

Examples of emergent gauge symmetry…

http://research.ipmu.jp/seminar/sysimg/seminar/1607.pdf

Gauge symmetries are properly to be thought of as not being symmetries at all, but rather redundancies in our description of the system 1. The true configuration space of a (3 + 1)- dimensional gauge theory is the quotient $\mathcal{A}^3/\mathcal{G}^3$ of gauge potentials in $A_0=0$ gauge modulo three-dimensional gauge transformations. When gauge degrees of freedom become anomalous, we find that they are not redundant after all.

Hamiltonian Interpretation of Anomalies by Philip Nelson and Luis Alvarez-Gaume

From the modern point of view, then, gauge symmetry is merely a useful redundancy for describing the physics of interacting massless particle of spin 1 or 2, tied to the specific formalism of Feynman diagrams, that makes locality and unitarity as manifest as possible.

https://arxiv.org/pdf/1612.02797.pdf

Gauge invariance is not physical. It is not observable and is not a symmetry of nature. Global symmetries are physical, since they have physical consequences, namely conservation of charge. That is, we measure the total charge in a region, and if nothing leaves that region, whenever we measure it again the total charge will be exactly the same. There is no such thing that you can actually measure associated with gauge invariance. We introduce gauge invariance to have a local description of massless spin-1 particles. The existence of these particles, with only two polarizations, is physical, but the gauge invariance is merely a redundancy of description we introduce to be able to describe the theory with a local Lagrangian. A few examples may help drive this point home. First of all, an easy way to see that gauge invariance is not physical is that we can choose any gauge, and the physics is going to be exactly the same. In fact, we have to choose a gauge to do any computations. Therefore, there cannot be any physics associated with this artificial symmetry.

Quantum Field Theory and the Standard Model by Matthew Schwartz

History

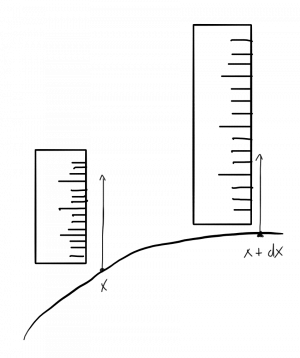The idea behind gauge symmetries emerged from an observation regarding electromagnetism and this is where the term gauge symmetry came from historically. Nowadays, the term Gauge Symmetry means internal symmetry of quantum fields, for example,

\begin{equation} \Psi(x) \rightarrow \mathrm{e}^{i \theta(x)} \Psi(x) \end{equation}

and the word "gauge" makes little sense.

Herrmann Weyl was one of the first who took symmetry ideas to the next level. He believed in the power of symmetry constraints and tried to derive electromagnetism in 1918 from invariance under local changes of length scale [1]. Nowadays, this is called scale invariance. For the invariance under changes of length scale, the name gauge symmetry is certainly appropriate. If one would change the object one used to define the length of a meter, at this time the Prototype Metre Bar, this would be a change of gauge and hence a change of length scale.

Weyl's attempt failed, but he was on the right track. Soon after he discovered the correct symmetry that enables the derivation of the correct theory of electromagnetism and the name stuck, despite making little sense in the new context.

Good books on the history of gauge theories are:

In 1932, Werner Heisenberg suggested the possibility that the known nucle- ons (the proton and the neutron) were, in fact, just two different “states” of the same particle and proposed a mathematical device for modeling this so-called isotopic spin state of a nucleon. Just as the phase of a charged particle is represented by a complex number of modulus 1 and phase changes are accomplished by the action of U (1) on S 1 (rotation) so the isotopic spin of a nucleon is represented by a pair of complex numbers whose squared moduli sum to 1 and changes in the isotopic spin state are accomplished by an action of SU (2) on S 3 . In 1954, C. N. Yang and R. L. Mills set about constructing a theory of isotopic spin that was strictly analogous to classical electromagnetic theory. They were led to consider matrix-valued potential functions (denoted B μ in [YM]) and corresponding fields (F μν in [YM]) constructed from the derivatives of the potential functions. The underlying physical assumption of the theory (gauge invariance) was that, when electromagnetic effects can be neglected, interactions between nucleons should be invariant under arbitrary and independent “rotation” of the isotopic spin state at each spacetime point. This is entirely analogous to the invariance of classical electromagnetic interactions under arbitrary phase changes (see Chapter 0) and has the effect of dictating the transformation properties of the potential functions B μ under a change of gauge and suggesting the appropriate combination of the B μ and their derivatives to act as the field F μν .Topology, Geometry and Gauge Fields: Foundations by Naber

advanced_tools/gauge_symmetry.txt · Last modified: 2020/04/02 20:12 by 95.90.205.199

Page Tools

Except where otherwise noted, content on this wiki is licensed under the following license: CC Attribution-Share Alike 4.0 International
CC Attribution-Share Alike 4.0 International Donate Powered by PHP Valid HTML5 Valid CSS Driven by DokuWiki