Intuitive

In quantum mechanics, we no longer describe the trajectories of individual particles but only talk about probabilities that certain events can happen. In the canonical description of quantum mechanics, we calculate these probabilities using a wave description for the particles.

So instead of describing the path between some points $A$ and $B$, we ask instead: "What's the probability that a particle which started at $A$ ends up at $B$?". Note that because particles are described by a wave, the points $A$ and $B$ will now correspond to points with highest probability of finding a particle there (being the highest point of the wave), as opposed to an exact point in space and time.

This idea of describing particles and their trajectories by waves is rooted in the observation that the only things that are actually important are those that we observe, the observation being any form of measurement. Whatever happens between two measurements is not important, since we do not measure it. So when we do not measure the position of the particle between $A$ and $B$ it could have taken any path.

While this sounds strange for everyday objects, this is the natural point of view for much tinier particles. We measure the position of a ball whenever we look at it. Such a measurement has no significant effect on the ball.

In contrast, for tiny particles like an electron every measurement has a huge effect on it and hence is important. In addition, we do not measure the electron position permanently but only at certain times.

More details

Let‘s imagine for a moment that quantum mechanics, Newton's classical mechanics, Maxwell‘s electrodynamics weren‘t discovered yet and we start thinking about nature. Not just nature, but nature at the most fundamental level. Basically, what the Greeks did 3000 years ago but with the power of hindsight.

Firstly, no matter how we may define fundamental it is quite rational to assume there are some basic building blocks everything else is made of. The Greeks called them atoms (Atomos is greek for indivisible), but because someone in the modern world decided to call something not fundamental atoms, we must use the slightly ugly notion of elementary particles.

Will the framework that is perfectly suited to describe everyday objects like a rolling ball be a good fit to describe elementary particles? How do we know something about the rolling ball?

Well, we need some light and then we look at it, film it with a camera or use some other sophisticated motion tracking device. We can do this all the time. Does the ball care about the lamp or the camera? Of course not! A ball does not behave differently in the dark.

How do we know something about elementary particles? Well, we need to measure. Of course, this is just a fancy term for the process described in the last paragraph, but it‘s a useful one as we will see. Again, we need some light and a camera. Does the elementary particle care about the lamp and the camera? Of course, it does!

The rolling ball would behave differently, too, if we measure its position by shooting tennis balls at it and analyze the direction of the tennis balls afterward.

That is not the usual measurement technique for rolling balls because we can shoot something much smaller at it that does not change its behavior. For fundamental particles, we have no choice.

Light itself consists of elementary particles, called Photons. To learn something about fundamental objects we have no choice, but to use objects of similar size. There is nothing smaller because that is how we define the fundamental scale.

Now we can prepare ourselves for some seemingly crazy property a theory describing nature at the most fundamental scale must have.

For the rolling ball, we can in principle compute how the rolling ball changes its momentum if we shoot tennis balls at it because we control the location and momentum of the tennis balls that we use to measure its properties, like its location and its momentum.

On the fundamental scale, we aren‘t able to control the particles we use to measure completely, because how would we do that? There is nothing smaller and every time we measure the properties of the particles that we use to measure, we change their properties. In addition, how should we know the properties of the particles that we use to measure the properties of the particles that we use it to measure?

On the fundamental scale, in order to measure we have no choice but to use particles of similar size. This process necessarily changes the properties of the particles in question, because again we can‘t control their properties completely.

Changing back to the macroscopic example, we can imagine what it would be like if we could only measure the location and momentum of the yellow tennis balls by shooting red tennis balls onto them. Then we could use blue tennis balls to measure the properties of the red balls, but how would we know their properties? As long as we have only tennis balls and nothing fundamentally smaller there is no way to measure their properties with arbitrary precision.

Of course for macroscopic objects, we have smaller things, but on the fundamental scale there is nothing smaller and this is why we will necessarily have some randomness to account for in our framework. In mathematical terms, this requires that we need to talk about probabilities.

Short disclaimer: Please don‘t get confused by the notion of size, because it‘s terribly ill-defined regarding elementary particles. Maybe more appropriate would be energy or momentum. I hope the message I‘m trying to bring across is clear no matter how we call it. Macroscopic objects, like a ball, don‘t change their behavior if we shoot elementary particles at them. In contrast, elementary particles behave differently when we shoot elementary particles at them and, unfortunately, in order to learn something about them we have no other choice.

For macroscopic objects there is no need to talk about measurements, because some photons crashing at the big ball aren‘t a big deal. Therefore a framework suited to describe a rolling ball works perfectly without anything that accounts for measurements.

It should be clear by now that the same framework is ill-suited for describing elementary particles.

Let‘s build a better framework. Remember, we know nothing about the conventional theories and want to start from scratch. We know nothing about an elementary particle until we measure its properties like its position or momentum. (The same is true of course for the rolling ball, but the statement is on the macroscopic scale trivial because when we talk about the position and momentum of the ball it‘s clear that we mean the position and momentum that we measure with the camera etc.)

Our framework must be able to account for the possibility that our measurement changes the properties of the particle in question. Therefore, we introduce measurement operators $\hat O$. For example, the momentum operator $\hat p$ or the position operator $\hat x$. (For macroscopic objects we can use ordinary numbers, but numbers do not really change anything. On the fundamental scale we need a mathematical concept that is able to change something.)

Next, we need something that describes the elementary particle or to be more general the physical system in question. Our framework should be able to describe lots of different situations and therefore we simply invent something abstract $| \Psi \rangle$, that describes the state of our physical system or of the elementary particle.

If we measure the momentum of an elementary particle, we have in our framework $\hat p | \Psi \rangle $. The measurement operator acts on the object that describes the elementary particle.

• A nice collection of explanations and videos is www.quantummadesimple.com
• For a nice, light-hearted book see "How to Teach Quantum Physics to Your Dog" by Chad Orzel
• An Intuitive Explanation of Quantum Mechanics by Eliezer_Yudkowsky

Concrete

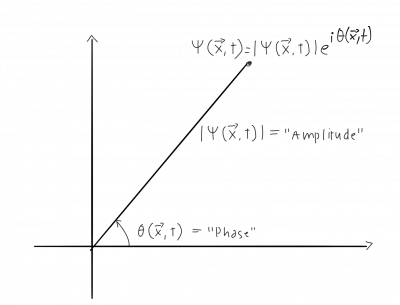
The state of a system in quantum mechanics is represented by a wave function $\Psi(\vec x,t)$. This wave function contains all the information about the system we are considering. The wave function is a complex number at each point in space and time and it is useful to write complex numbers in polar form

Let's assume our system is just an electron. The wave function contains all the information about this electron. Now, for each fixed point in time $t$, the probability to find our electron in some region $R$ is

$$ \int_R dV |\Psi(\vec x,t)|^2 .$$

We get the wave function that describes the system in question by solving the Schrödinger equation. The object in the Schrödinger equation that describes the system in question is the Hamiltonian and the boundary conditions.

A short introduction

At the heart of quantum mechanics is the idea that we know nothing about an elementary particle until we measure its properties like position or momentum. (The same is true of course for a big object, like a rolling ball, but the statement is on the macroscopic scale trivial, because when we talk about the position and momentum of the ball it‘s clear that we mean the position and momentum that we measure with a camera etc.)

Our quantum framework must be able to account for the possibility that our measurement changes the properties of the particle in question. Therefore, we introduce measurement operators $\hat O$. For example, the momentum operator $\hat p$ or the position operator $\hat x$. (For macroscopic objects we can use ordinary numbers, but numbers do not really change anything. On the fundamental scale we need a mathematical concept that is able to change something.)

Next, we need something that describes the elementary particle or to be more general the physical system in question. Our framework should be able to describe lots of different situations and therefore we simply invent something abstract $| \Psi \rangle$, that describes the state of our physical system or of the elementary particle.

If we measure the momentum of an elementary particle, we have in our framework $\hat p | \Psi \rangle $. The measurement operator acts on the object that describes the elementary particle. Okay, what now?

Firstly, operators have abstract (!) eigenvectors and eigenvalues. Famous examples are matrices, but be aware of the fact that not every operator in mathematics is a matrix. The definition of an eigenvector is that it is unchanged by the corresponding operator. Concretely this means $$ \hat O | o\rangle = E_o | o\rangle, $$

if $ | o\rangle $ is an eigenvector of $\hat O$ and $E_o$ is the corresponding eigenvalue. In contrast, for a general, abstract vector $ | x\rangle$, we have $$ \hat O | x\rangle = z | y \rangle. $$

The number of eigenvectors and eigenvalues depends on the operator and in physics often we will have to deal with infinitely many. Does this sound strange?

It shouldn‘t, because how else should we interpret the eigenvalues of a measurement operator, if not as the actual numbers we measure in experiments? There are infinitely many different momenta we can measure and therefore we need an infinite number of eigenvalues and eigenvectors for the momentum operator. (You‘ll learn soon enough what an operator with an infinite number of eigenvalues looks like.)

Back to our framework, what can we say about our abstract $| \Psi \rangle$ we introduced in order to account for our elementary particle or physical system? The crucial ingredient of our framework are the measurement operators.

Every operator has a set of eigenvectors, which form a basis for the corresponding vector space. The abstract $| \Psi \rangle$ must live in this vector space, because otherwise acting with the measurement operators on it makes no sense and we conclude that $| \Psi \rangle$ are vectors in an abstract sense.

The defining feature of a basis is that we can write every element of this vector space, which includes $| \Psi \rangle$, as a linear combination of eigenvectors.

For a general $| \Psi \rangle$ we have

$$ \hat O | \Psi \rangle = | \Phi \rangle, $$

because in general $| \Psi \rangle$ is no eigenvector of $\hat O $. Nevertheless, we can write

$$ | \Psi \rangle = \sum_o c_o | o\rangle , $$

with some numbers $c_o$ that are called the coefficients in this series expansion. This yields

\begin{align} \hat O | \Psi \rangle &= \hat O \sum_o c_o | o \rangle \notag \\ &= \sum_o c_o \hat O | o \rangle \notag \\ &= \sum_o c_o E_o | o \rangle \notag \\ &= \sum_o d_o | o \rangle \notag \\ &= |\Phi \rangle , \end{align}

which we can see as a series expansion of $|\Phi \rangle$ in terms of the basis $ | o\rangle $, with now different coefficients $d_o$.

That may seem like a lot of unnecessary yada yada. Maybe you wonder: Why all this talk about general things like $|\Psi \rangle$? Don‘t we only need eigenvectors where we get some easy answer when we act on it with our operators?

If the eigenvalues are the result of our measurements, what does something like $ \sum_o c_o E_o | o\rangle$ mean? If we measure the momentum of an elementary particle, we get a definite number and here in the formalism we get wild sum.

You're right! Of course, as long as we don‘t measure the properties of our elementary particle, we don‘t know its properties and therefore we need a sum that includes all possibilities to describe it.

The same is true for an ordinary rolling ball. If we have an elementary particle with definite momentum, which we can adjust for example with magnetic fields, and then measure its momentum, we get of course just a number: its momentum. An elementary particle with prepared definite momentum, say $4 \frac{kg m}{s}$ is of course described by an eigenvector $| 4 \frac{kg m}{s} \rangle$ of the momentum operator $ \hat p$ and we have

$$ \hat p | 4 \frac{kg m}{s} \rangle = 4 \frac{kg m}{s} | 4 \frac{kg m}{s} \rangle. $$

For situations like this our formalism is really easy and works as we would expect it, but now prepare for a big surprise!

Operators have some curious feature that ordinary numbers do not have. If we have two operators $ \hat p $ and $ \hat x $ with different eigenvectors $| p\rangle$ and $| x\rangle$, we have in general $$ \hat p \hat x | x\rangle \neq \hat x \hat p | x\rangle , $$

because $ | x\rangle$ is not an eigenvector of $\hat p $ and therefore we have $\hat p | x\rangle= z | y\rangle$. We have on the one hand: $$ \hat x \hat p | x\rangle = \hat x z | y\rangle \text{ and on the other hand } \hat p \hat x | x\rangle = \hat p E_x | x\rangle$$

There is no reason why these two terms should be the same and in general they are really different. (There are operator pairs where $ \hat O_1 \hat O_2 | x\rangle = \hat O_2 \hat O_1 | x\rangle$, but in general this is not the case.)

What does this mean? Translated into words this means that a measurement of the location, followed by a measurement of the momentum is in general something different than a measurement of the momentum followed by a measurement of the location. A measurement of the location changes the location and vice versa!

We already talked about how on a fundamental scale we can‘t expect that our measurement does not change anything, but what we have here isn‘t some effect that appears because our experiment was designed poorly. It is intrinsic! We are always changing the location if we measure the momentum.

There is no way to avoid this and this is why we need to talk about general, abstract things like $|\Phi \rangle$.

As explained above, we can prepare our particle with definite momentum and we get a simple answer if we act with our measurement operator on the corresponding vector. But what if we want to know its location, too?

An eigenvector of $ \hat x $ is not necessarily and eigenvector of $ \hat p$ and therefore acting with $ \hat x $ on our carefully prepared particle results in a big question mark:

$$ \hat x |4 \frac{kg m}{s} \rangle = ? $$

We can expand $ |4 \frac{kg m}{s} \rangle $ in terms of eigenvectors of $\hat x$ and then the question mark turns into a sum:

$$ \hat x |4 \frac{kg m}{s} \rangle = \sum_x c_x \hat x |x \rangle = \sum_x c_x \hat x |x \rangle = \sum_x c_x E_x |x \rangle. $$

All these to come to a dead end? We must find some interpretation for this if we want to make sense of our framework.

Let‘s recap how we got here. We started by thinking about one crucial feature our framework must include: Measurements.

This led us to the notion of a measurement operator, which must be one of the cornerstones of our framework, because we know nothing until we measure. Then we took a look at what mathematics can tell us about operators and we learned many things that make a lot of sense. Unfortunately, the last feature is somewhat weird.

Happily, there is another mathematical idea that will help us make sense of all this: If we have a vector space, we must have some scalar product. This means it‘s possible to combine two vectors in such a way that the result is an ordinary, possibly complex, number.

For the moment don‘t worry about the details, just imagine some trustworthy mathematician told you and now we want to think about the physical interpretation.

Not caring about any details, we denote our scalar product of two vectors $ |y \rangle$ and $ |z \rangle$ abstractly:

$$ \langle z| |y \rangle = \text{ some number} $$

The bases we talked about earlier have the nice feature of being orthogonal, which means we have

$$ \langle o‘| |o \rangle = 0 $$

unless $o‘ =o$, then we have

$$ \langle o| |o \rangle = \text{ some number} . $$

Going back to our example from above we can now see that this is exactly the missing puzzle piece. We have a sum that we couldn‘t interpret in any sensible way:

$$ \sum_x c_x E_x |x \rangle . $$

Recall what we mean by $ |x \rangle$. We use the abstract eigenvector $|x \rangle$ to describe an elementary particle at position $x$.

For example, if we had prepared the location $x=5$ cm, using some coordinate system, instead of the momentum, we would have $|5 cm \rangle$ as an abstract object that describes our particle. But we decided to prepare our particle with definite momentum and therefore we describe it by a momentum eigenvector: $|4 \frac{kg m}{s} \rangle$.

Acting with the location operator on this eigenvector results in the sum. Now we can multiply $ \hat x |4 \frac{kg m}{s} \rangle $ with for example $\langle5 cm |$, which means we compute the scalar product and make sense of the big question mark because the result will be a number instead of a sum of many, many vectors! We have

$$ \langle5 cm | \hat x |4 \frac{kg m}{s} \rangle = \langle5 cm| \sum_x c_x E_x |x \rangle = \sum_x c_x E_x \langle5 cm | |x \rangle $$

Every term in this sum is zero except for $|x \rangle= |5 cm \rangle$ and therefore we have

\begin{align} 5 cm | \hat x |4 \frac{kg m}{s} \rangle &= \langle5 cm| \sum_x c_x E_x |x \rangle \\ &= \sum_x c_x E_x \langle5 cm | |x \rangle \\ &= c_{5 cm} E_{5 cm} \langle5 cm | |5 cm \rangle \\ &= c_{5 cm} E_{5 cm} \times \text{ some number} \end{align}

Still confused? The sum has gone away because we multiplied it with the vector that we would use to describe a particle sitting at the definite location $x=5$ cm. We can do the same with vectors for different locations like $|7 cm \rangle$ or $|99 cm \rangle$ and get a different number.

These numbers are the probability amplitudes for measuring that the particle we prepared with momentum $4 \frac{kg m}{s}$ sits at $x=5$ cm, $x=7$ cm or $x=99$ cm.

Of course, it is strange that we must now talk about probabilities, but please keep in mind how we got here.

Mathematics tells us that the position and momentum operators have different eigenvectors. Therefore each time we measure the location we change the momentum and vice versa.

This is exactly what we expect from the discussion at the beginning. Just think about measuring the location of a rolling ball by shooting tennis balls at it. Of course, this will change its momentum and if we could only determine the properties of the tennis balls, by using different tennis balls, we would need to talk about probabilities, too.

There are still a lot of things of missing to transform our rough framework into an actual physical theory. For example, we must know how our vectors change in time. This is what the Schrödinger equation tells you and you will spend a lot of time-solving it for different situations.

Examples

Example: Particle in a box

Image by Bdesham published under a CC BY-SA 3.0 licence (https://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons

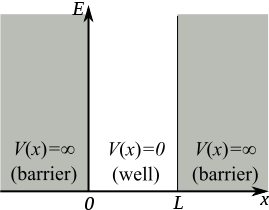
A particle confined in a box, here 1-dimensional, with infinitely high potential walls is one of the standard examples of quantum mechanics. Inside the box the potential is zero, outside it's infinite.

The potential is defined piece-wise

\begin{equation} V = \left\{ \begin{array}{ll} 0, & 0< x <L \\ \infty, & {\mathrm{\ otherwise }} \end{array} \right. \end{equation} and therefore, we have to solve the one-dimensional Schrödinger equation piece-wise. \[ i \partial_t \Psi(\vec{x},t) = -\frac{\partial_x^2}{2m} \Psi(x,t) + V(x) \Psi(x,t) \]

• Inside the box, the solution is equal to the free particle solution, because $V=0$ for $0< x <L$
• Outside, because $V=\infty$, the only possible, physical solution is $\Psi(x,t)=0$.

We can rewrite the general free particle solution \[ \Psi(x,t) = A {\mathrm{e }}^{-i ( E t - \vec p \cdot \vec x) } + B {\mathrm{e }}^{-i ( E t + \vec p \cdot \vec x) } \] \[ = \big( C \sin(\vec p \cdot \vec x) + D \cos(\vec p \cdot \vec x) \big){\mathrm{e }}^{-i E t}, \] which we can rewrite again using the non-relativistic energy-momentum relation \[ E = \frac{\vec{p}^2}{2m} \qquad \rightarrow \qquad \vec p = \sqrt{2mE} \] \begin{equation} \Psi(x,t) = \big( C \sin(\sqrt{2mE}x) + D \cos(\sqrt{2mE}x) \big){\mathrm{e }}^{-i E t} \end{equation}

Next, we use that the wave-function must be a continuous function\footnote{If there are any jumps in the wave-function, the momentum of the particle $ \hat p_x \Psi = -i \partial_x \Psi$ is infinite because the derivative at the jumping point would be infinite.}. Therefore, we have the boundary conditions $\Psi(0)=\Psi(L) \stackrel{!}{=} 0$. We see that, because $\cos(0)=1$ we have $D\stackrel{!}{=}0$. Furthermore, we see that these conditions impose \begin{equation} \label{box:quantbed} \sqrt{2mE}\stackrel{!}{=} \frac{n \pi}{L}, \end{equation} with arbitrary integer $n$, because for\footnote{Take note that we put an index $n$ to our wave-function, because we have a different solution for each $n$.}

\begin{equation} \label{eq:energyeigenfunctions} \Phi_n(x,t)=C\sin(\frac{n \pi}{L} x){\mathrm{e }}^{-i E_n t} \end{equation} both boundary conditions are satisfied \[\rightarrow \Phi_n(L,t)=C\sin(\frac{n \pi}{L} L){\mathrm{e }}^{-i E t} = C\sin(n \pi){\mathrm{e }}^{-i E t} =0 \qquad \checkmark \] \[\rightarrow \Phi_n(0,t)= C \sin(\frac{n \pi}{L} 0){\mathrm{e }}^{-i E t} = C\sin(0){\mathrm{e }}^{-i E t} =0 \qquad \checkmark \] The normalization constant $C$, can be found to be $C=\sqrt{\frac{2}{L}}$, because the probability for finding the particle anywhere inside the box must be $100\%=1$ and the probability outside is zero, because there we have $\Psi=0$. Therefore \[ P= \int_0^L dx \Phi_n^\star(x,t) \Phi_n(x,t) \stackrel{!}{=} 1 \] \[P = \int_0^L dx C^2 \sin(\frac{n \pi}{L} x){\mathrm{e }}^{+i E t} \sin(\frac{n \pi}{L} x){\mathrm{e }}^{-i E t} \] \[ = C^2 \int_0^L dx \sin^2(\frac{n \pi}{L} x) = C^2 \left[\frac{x}{2} -\frac{\sin (\frac{2n \pi}{L} x)}{4 \frac{n \pi}{L}} \right]_0^L \] \[ = C^2 \left( \frac{L}{2} - \frac{\sin (\frac{2n \pi}{L} L)}{4 \frac{n \pi}{L}} \right) = C^2 \frac{L}{2} \stackrel{!}{=} 1 \] \[ \rightarrow C^2 \stackrel{!}{=} \frac{2}{L} \qquad \checkmark \] We can now solve Eq.~\ref{box:quantbed} for the energy $E$

\begin{equation} E_n \stackrel{!}{=} \frac{n^2 \pi^2}{L^2 2m}. \end{equation} The possible energies are quantized, which means that the corresponding quantity can only be integer multiplies of some constant, here $ \frac{ \pi^2}{L^2 2m}$. Hence the name quantum mechanics.

Take note that we have a solution for each $n$ and linear combinations of the form \[ \Phi(x,t) = A \Phi_1(x,t) + B \Phi_2(x,t) + \ldots \] are solutions, too. These solutions have to be normalised again because of the probabilistic interpretation\footnote{A probability of more than $1=100\%$ doesn't make sense}.

The best beginner quantum mechanics textbooks are

• Feynman Lectures on Physics Vol. 3
• Griffiths - Quantum Mechanics
• Thaller - Visual Quantum Mechanics
• The Picture Book of Quantum Mechanics by Brandt, Siegmund, Dahmen, Hans Dieter
• Modern Quantum Mechanics by Jun John Sakurai
• The Principles of Quantum Mechanics by Paul Dirac
• Nice free lecture notes can be found here.
• See also A Cavendish Quantum Mechanics Primer by M. Warner, FRS & A. C. H. Cheung which is a very gentle introduction aimed at highschool students.

The standard textbook is Quantum Mechanics by Claude Cohen-Tannoudji, Bernard Diu und Franck Laloë.

See also: Nine formulations of quantum mechanics by Daniel F. Styer, et. al. and this StackExchange answer.

Abstract

Mathematically canonical quantum mechanics is analysis of unitary (self-adjoint) operators acting on Hilbert spaces.

Remarkably, in quantum mechanics the analog of Noether’s theorem follows immediately from the very definition of what a quantum theory is. This definition is subtle and requires some mathematical sophistication, but once one has it in hand, it is obvious that symmetries are behind the basic observables. Here’s an outline of how this works, (maybe best skipped if you haven’t studied linear algebra…) Quantum mechanics describes the possible states of the world by vectors, and observable quantities by operators that act on these vectors (one can explicitly write these as matrices). A transformation on the state vectors coming from a symmetry of the world has the property of “unitarity”: it preserves lengths. Simple linear algebra shows that a matrix with this length-preserving property must come from exponentiating a matrix with the special property of being “self-adjoint” (the complex conjugate of the matrix is the transposed matrix). So, to any symmetry, one gets a self-adjoint operator called the “infinitesimal generator” of the symmetry and taking its exponential gives a symmetry transformation.

One of the most mysterious basic aspects of quantum mechanics is that observable quantities correspond precisely to such self-adjoint operators, so these infinitesimal generators are observables. Energy is the operator that infinitesimally generates time translations (this is one way of stating Schrodinger’s equation), momentum operators generate spatial translations, angular momentum operators generate rotations, and the charge operator generates phase transformations on the states.

The mathematics at work here is known as “representation theory”, which is a subject that shows up as a unifying principle throughout disparate area of mathematics, from geometry to number theory. This mysterious coherence between fundamental physics and mathematics is a fascinating phenomenon of great elegance and beauty, the depth of which we still have yet to sound.http://www.math.columbia.edu/~woit/wordpress/?p=4385

From a mathematician’s point of view, the simplest representations to look at are unitary representations on a complex vector space, so the mathematical structure of quantum mechanics is very natural. To each symmetry generator you get a conserved quantity, and it appears in quantum mechanics as the thing you exponentiate (a self-adjoint operator) to get a unitary representation. http://www.math.columbia.edu/~woit/wordpress/?p=4033

The best abstract quantum mechanics textbooks are

• Foundations of Quantum Mechanics by Gregory Naber for students who prefer a more mathematical treatment.
• Quantum Theory: Concepts and Methods by Asher Peres
• Quantum Mechanics by L. E. Ballentine
• Quantum Theory, Groups and Representations - An Introduction by Peter Woit
• Quantum Theory for Mathematicians by Brian Hall
• "An Introduction to the Mathematical Structur of Quantum Mechanics" by F. Strocchi
• Josef M. Jauch, Foundations of Quantum Mechanics, Addison-Wesley, 1968.
• George Mackey, The Mathematical Foundations of Quantum Mechanics, Dover, New York, 1963.
• Picturing Quantum Processes: A First Course in Quantum Theory and Diagrammatic Reasoning by Bob Coecke and Aleks Kissinger

See also the discussion on the question "Where does a math person go to learn quantum mechanics?" at mathoverflow.

Recommended Further Reading:

• Quantum Mechanics: New Approaches to Selected Topics by H. Lipkin
• Common misconceptions regarding quantum mechanics by Daniel F. Styer
• Kindergarten Quantum Mechanics by Bob Coecke
• "Quantization is a mystery" by Ivan Todorov
• Demystifying Quantum Mechanics: A Simple Universe with Quantum Uncertainty by Gary L. Drescher
• Mathematical surprises and Dirac's formalism in quantum mechanics by F. Gieres
• Quantum mechanics: Myths and facts by Hrvoje Nikoli´c
• R. Medina, “Orthodox quantum mechanics free from paradoxes,” quant-ph/0508014.
• N. D. Mermin, “What is quantum mechanics trying to tell us?,” Am. J. Phys. 66 (9), 753-767 (1998).
• Geometrical Formulation of Quantum Mechanics by Abhay Ashtekar and Troy A. Schilling
• Classical and quantum mechanics via Lie algebras by Arnold Neumaier Dennis Westra
• Quantum Mechanics and Quantum Field Theory: A Mathematical Primer by J. Dimock

Why is it interesting?

Quantum mechanics is a better approximate description of nature than classical mechanics.

When things get tough, there are two things that make life worth living: Mozart, and quantum mechanics Victor Weisskopf

For those who are not shocked when they first come across quantum theory cannot possibly have understood it. Niels Bohr, in 1952, quoted in Heisenberg, Werner (1971). Physics and Beyond. New York: Harper and Row. pp. 206.

It is often stated that of all the theories proposed in this century, the silliest is quantum theory. In fact, some say that the only thing that quantum theory has going for it is that it is unquestionably correct. Michio Kaku, in Hyperspace (1995), p. 263

FAQ

Why is the Hamiltonian required to be self-adjoint?

I was asked to discuss the particle in a piecewise constant potential (and compute reflection and transmission coefficients etc). I was asked why I picked particular boundary conditions of my wave function at the jumps of the potential. Luckily, instead of parroting what I had read in some textbook ('the probability current has to be continuous so no probability gets lost') I had one of my very few bright moments and realised (I promise I came up with this myself, I had not heard or read it before) that this comes from requiring the Hamiltonian (esp. the kinetic term) to be self-adjoined: If you check this property, you have to integrate by parts and the boundary terms vanish exactly if you assume the appropriate continuity conditions of the wave function.https://atdotde.blogspot.de/2006/09/

Where do the quantum operators come from?

[Wigner] interpreted the infinitesimal space and time translations as operators of total momentum and of total energy, and therefore (later on) restricted his attention to representations in which the energy-momentum lies in or on the plus light-cone; that is the spectral condition. He classified the irreducible representations satisfying the spectral condition.

The usefulness of a general theory of quantized fields by A. S. WIGHTMAN

In quantum mechanics, conserved quantities then become the generators of the symmetry.

lecturenotes232.pdf

This is discussed in section 3.4. of Ballentine's Quantum Mechanics book, where he basically presents the idea of Jordan's "Why −i∇ is the momentum"

Equations

The Schrödinger equation

$$i \hbar \partial_t \Psi(x,t) = H \Psi (x,t) $$

that describes the time-evolution of the wave function. The time-independent version for systems where the Hamiltonian is time-independent is given by

$$H \psi(x)= E\psi(x),$$ where the complete wave function $\Psi$ is then given by

$${\Psi(x,t) = \phi(t) \psi(x) = e^{-Et/\hbar} \psi(x)}$$

The standard Hamiltonian is

$$ H = - \frac{\hbar^2}{2m} \Delta^2 + \hat V \hat{=} \frac{\hat{p}^2}{2m} +\hat{V}. $$

The Heisenberg equation

$$\frac{\mathrm{d}\hat F}{\mathrm{d}t} = -\frac{i}{\hbar}[\hat F,\hat H] + \frac{\partial \hat F}{\partial t},$$

which described the time-evolution of operators and the related time dependence of an expectation value

$$ \langle \frac{\mathrm{d}\hat F}{\mathrm{d}t} \rangle = \langle -\frac{i}{\hbar}[\hat F,\hat H] \rangle + \langle \frac{\partial \hat F}{\partial t} \rangle .$$

The uncertainty principle

$$ \sigma_x \sigma_p \geq \hbar/2,$$

and the generalized version

$$ \sigma_A \sigma_B \geq \big | \frac{1}{2i} \langle [A,B] \rangle \big|^2 .$$

The canonical commutation relations

$$ [\hat{p},\hat{x}] = -i \hbar .$$