Intuitive

The basic idea of the Lagrangian formalism can be summarized by the statement:

Nature is lazy.

The laziness of nature is demonstrated nicely by how light behaves.

The Principle of Least Time

Long before Joseph Lagrange invented the formalism now named after him, it was well known that light always takes the path between two points that requires the least travel time. This is known as Fermat's Principle.

Nature operates by means and ways that are easiest and fastest.Pierre de Fermat

In a vacuum, light travels in a straight path between two points: the least time required.

However, it gets more interesting when we have a medium present.

Which path will the light take from a point outside of the medium $A$ to a point $B$ inside the medium?

It still takes the path with the least travel time! However, properties of the medium may cause the path to be different than a straight line. A common situation when paths are not straight is when objects span two different media - appearing to be 'broken'. (For example, a spoon in a glass of lemonade.)

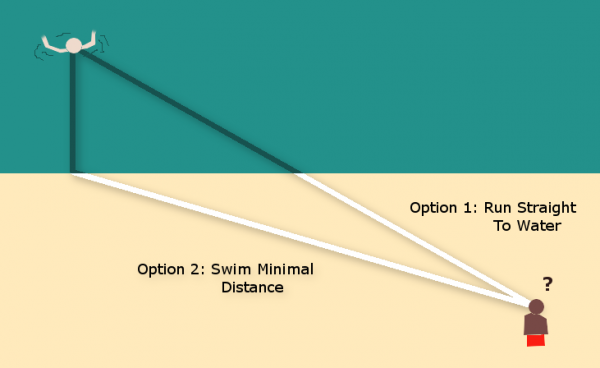
To understand this let's consider a rescue swimmer who sees someone drowning in the water. Which path should he take to get to the swimmer as fast as possible? He is slow in the water and fast running on the beach. This gives him two extreme options:

• Should he run straight to the water and then start swimming?
• Should he run on the sand until he has to swim the minimal distance?

OR is there some better option?

There is. The optimal path is a trade-off of the two choices above. While it is true that the rescuer is much faster on the sand, the path in Option 2, above, is much longer than if he runs and swims diagonally.

This is exactly the same behaviour light has. From Fermat's principle, we can now see why light gets broken across two media: Light is slower in the media and thus has to choose a trade-off between a minimal total path length and a minimal length in the slower medium.

Reading Recommendations

• To Save Drowning People, Ask Yourself “What Would Light Do?” by Aatish Bhatia

Concrete

To exploit the idea that nature is lazy, we need to define some quantity that measures "laziness". We name this quantity the "action" of a system. A system with bigger "action" is less lazy than a system with small "action". The "action" is the sum of the difference between the kinetic and potential energy for all "timesteps" in a given interval. The difference between the kinetic and the potential energy is called the Lagrangian. For every point in time $t$, the Lagrangian has some value $L(t)$. Let's say we want to analyze a system for 5 seconds. The action of the system is the sum of all values of the Lagrangian during these five seconds. In mathematical terms, the action is therefore the integral of the Lagrangian function $L(t)$, starting at some $t_0$ and ending at some $t_1$:

$$ \text{Action} = \int_{t_0}^{t_1} L(t) dt $$

The statement that nature is lazy means now in mathematical terms that during some given time span, here from $t_0$ to $t_1$, the system behaves in such a way that the action is as small as possible. This is known as the principle of minimal action.

Whenever any change takes place in Nature, the amount of action expended in this change is always the smallest possible.Pierre Louis Maupertuis

So, why is the laziness of a system given by the difference between the kinetic and potential energy?

The kinetic energy is a measure for how much is happening, i.e. how much activity is going on in the system. The potential energy, as the name indicates, is a measure for how much activity could potentially happen, but does not. A good example is a ball at the top of a cliff. At this point its potential energy is maximal, but could be converted to kinetic energy at any moment if it slides down the cliff.

In other words, the Lagrangian measures how much is happening, minus how much could be happening but isn't.

Let's consider an explicit example: We throw a ball and want to know what path it will follow between two given points $A$ and $B$ on the ground, where it starts at a fixed time $t_A$ and ends up on the ground at fixed time $t_B$.

The correct path is, of course, a parabola, but we can understand this path from the principle of minimal action, i.e. minimal activity, i.e. maximal laziness principle:

If the ball is high above the ground its potential energy is large and this is something that nature likes according to the principle of maximal laziness. There $T-V$ is small and this is what we should minimize according to this principle. That's why the ball spends as much time as possible high above the ground.

However, it can't spend too much time there, because otherwise it must move incredibly fast up and down to this position. The price for this would be an incredibly high kinetic energy, which nature dislikes.

Thus, the principle of minimal action does not simply mean that potential energy gets maximized, but that we have a trade off. Nature tries to make the potential energy as large as possible, while keeping the kinetic energy at a reasonable value. This explains why the ball almost stops at the top, and is the fastest close to the ground.

Now with all this in mind, let's revisit the example discussed in the "Intuitive" section.

Light Again

In mathematical terms, we can formulate the observation that light takes the shortest paths between two points as follows:

The travel time for a path $q(t)$ between two fixed points $A$ and $B$ is given by

\[S_{\text{light}}[q(t)]=\int_A^B dt\]

The path $q_m(t)$ that light actually takes is the path that minimizes this quantity. For light this quantity is simply the travel time.

This is certainly an attractive explanation for the behaviour of light. If you could design a universe with physical laws, what other path would you let light take between two points?

Now, Joseph Lagrange was fascinated by this principle and tried to find something similar for other objects, not just light. Unfortunately, simply assuming that the correct path for general objects is the path with minimal travel time does not yield correct results.

However, Lagrange instead proposed a more general ansatz

\[S[q(t)]=\int L \,dt, \]

and that the correct path of every object can be found, by demanding that this quantity gets minimized. The task is then, of course, to find the correct quantity $L$, now called the Lagrange function. See Landau Mechanics, Volume 1, section 4 and 5 for the derivation of $L = T - V$ for classical objects.

Nevertheless, the exact same principle is so powerful that it is used in almost all modern theories.

For example, in quantum field theory, we also "guess" the correct function $L$ and find the correct equations of motion by minimizing the action $S$. The most powerful tool that we have in finding the correct quantity $L$ is symmetries. Experimental restrictions, such as the observation that the speed of light is constant in inertial frames of reference, are so powerful that they are almost enough to determine the correct function $L$.

"First, note that total energy is conserved, so energy can slosh back and forth between kinetic and potential forms. The Lagrangian L = K − V is big when most of the energy is in kinetic form, and small when most of the energy is in potential form. Kinetic energy measures how much is ‘happening’ — how much our system is moving around. Potential energy measures how much could happen, but isn’t yet — that’s what the word ‘potential’ means. (Imagine a big rock sitting on top of a cliff, with the potential to fall down.) So, the Lagrangian measures something we could vaguely refer to as the ‘activity’ or ‘liveliness’ of a system: the higher the kinetic energy the more lively the system, the higher the potential energy the less lively. So, we’re being told that nature likes to minimize the total of ‘liveliness’ over time: that is, the total action. In other words, nature is as lazy as possible!"http://math.ucr.edu/home/baez/classical/texfiles/2005/book/classical.pdf

Take note the Lagrange density could, in principle, be anything. However, most of the time its actual form is dictated by symmetry considerations.

Recommended Resources to learn more about the Lagrangian Formalism

• Least action visualized
• A great book to learn more about the Lagrangian from this perspective is The Lazy Universe by Jennifer Coopersmith
• To understand how the Lagrangian formalism is used in mechanics, "Introduction to Classical Mechanics" by David Morin is highly recommended.
• Another illuminating read is Action: Forcing Energy to Predict Motion by Dwight E. Neuenschwander
• For a nice description of minimization principles see page 7ff in Lectures on Classical Mechanics, by John Baez
• ANNOTATED BIBLIOGRAPHY ON THE PRINCIPLE OF LEAST ACTION by Edwin F. Taylor

The momentum of our particle is defined to be p = dL/dq'. The force on it is defined to be F = dL/dq. The equations of motion - the so-called Euler-Lagrange equations - say that the rate of change of momentum equals the force: p' = F. That's how Lagrangians work!"

http://math.ucr.edu/home/baez//noether.html

Abstract

The geometry that underlies the physics of Hamilton and Lagrange’s classical mechanics and classical field theory has long been identified: this is symplectic geometry [Arnold 89] and variational calculus on jet bundles [Anderson 89, Olver 93]. In these theories, configuration spaces of physical systems are differentiable manifolds, possibly infinite-dimensional, and the physical dynamics is all encoded by way of certain globally defined differential forms on these spaces. https://arxiv.org/abs/1601.05956

Basic Idea:

In the Lagrangian approach we focus on the position and velocity of a particle, and compute what the particle does starting from the Lagrangian $L(q, \dot{q})$, which is a function

$$ L\colon TQ \to \mathbb{R} $$

where the tangent bundle is the space of position-velocity pairs. But we're led to consider momentum

$$ p_i = \frac{\partial L}{\partial \dot{q}^i} $$

since the equations of motion tell us how it changes

$$ \frac{d p_i}{d t} = \frac{\partial L}{\partial q^i} .$$

page 52 in http://math.ucr.edu/home/baez/classical/texfiles/2005/book/classical.pdf

Recommended Resources to learn more about the Lagrangian Formalism:

• page 491ff in Road to Reality by R. Penrose,
• page 167 in Geometric Methods of Mathematical Physics by B. Schutz and
• http://philsci-archive.pitt.edu/2362/1/Part1ButterfForBub.pdf.
• Bleecker, D., Gauge Theory and Variational Principles, Addison-Wesley, Reading, MA, 1981.
• Variational Principles in Dynamics and Quantum Theory by Wolfgang Yourgrau,Stanley Mandelstam

Why is it interesting?

The Lagrangian formalism is an almost universal framework that is applicable in most branches of physics. It's especially useful whenever we try to exploit symmetries to make problems simpler.

It was invented originally as an alternative to Newton's classical mechanics, but is now an essential part of the best theory of physics that we have.

The reason for the popularity is that it turns out guessing the correct equations that describe nature at the most fundamental level isn't a very good method, because the human intuition fails on this scale. The Lagrangian formalism makes it possible to derive the correct equations systematically.

In simple terms the Lagrangian, the most important thing in this formalism, is the object that we use to derive the fundamental equations.

We want equations that look the same for every observer, because otherwise our equations would be useless. Therefore, we have the strong condition that our Lagrangian must not only look the same for different observers, but must stay exactly the same. Otherwise we would get different equations.

This helps immensely and rules out a lot of possibilities.

Formulated differently: The Lagrangian formalism is the perfect framework to work with symmetries and symmetries are the best thing that we can use to derive the fundamental equations of nature instead of guessing.

"In modern attempts at fundamental physics, when some suggested new theory is put forward, it is almost invariably given in the form of some Lagrangian functional. This has many advantages, such as the fact that there is a greater chance (but not an absolute certainty) of the resulting theory having required consistency and invariance properties, and that some form of 'Newton's third law' is implicit (in the sense that if two field interact then the interaction is mutual: if one acts upon the other, then the other acts equally back on the one). Moreover, Lagrangians have the pleasant property that, if a new field is introduced, then its contributions can usually simply be added to the Lagrangian that one had before, with any required interaction terms added also. More importantly, perhaps, there is a direct route to the formulation of a quantum theory, via the path integral approach." page 491 in Road to Reality by R. Penrose

But why the Lagrangian formalism? Why do we enumerate possible theories by giving their Lagrangians rather than by writing down Hamiltonians? I think the reason for this is that it is only in the Lagrangian formalism (or more generally the action formalism) that symmetries imply the existence of Lie algebras of suitable quantum operators, and you need these Lie algebras to make sensible quantum theories. In particular, the S-matrix will be Lorentz invariant if there is a set of 10 sufficiently smooth operators satisfying the commutation relations of the inhomogeneous Lorentz group. It's not trivial to write down a Hamiltonian that will give you a Lorentz invariant S-matrix - it's not so easy to think of the Coulomb potential just on the basis of Lorentz invariance - but if you start with a Lorentz invariant Lagrangian density then because of Noether's theorem the Lorentz invariance of the *S-matrix is automatic.

What is Quantum Field Theory, and What Did We Think It Is? by Steven Weinberg

FAQ

Why is the classical Lagrangian the difference of kinetic and potential energy?

This can be derived from the correct Lagrangian of special relativity:

But how do we know this? Why is the Lagrangian given by such a strange combination? The reason is pretty non-trivial and illustrates the point that exact theories make more sense than approximate ones. Let us first consider the non-relativistic free particle for which the action is an integral over the kinetic energy. It is not very clear why minimizing this quantity should have any physical significance. But let us next consider the special relativistic free particle following a worldline in spacetime along some arbitrary curve with speed v(t). We attach a clock to the particle and ask how much time (Δ τ) will elapse in this moving clock, when a stationary clock in the lab frame S shows a lapse of Δt. At any instant t, the particle is momentarily at rest in a comoving Lorentz frame (S') boosted with respect to S by some velocity v(t). Since the interval $ds^2 = -c^2dt^2 +dx^2$ has the same value in all Lorentz frames, we can evaluate it in S and (S') and equate the results. In the comoving frame of the clock (S'), we have $ds^2 = -c^2dτ^2$ since $dx^2 = 0$, while in $S$, we have $ds^2 = -c^2dt^2 +dx^2 = -c^2dt^2[1-v^2(t)/c^2]$. So we get: $$ \tau = \int dt (1 - v^2(t)/c^2)^{1/2} $$ which — called the proper time — is clearly an invariant quantity. Note that this expression is valid for clocks in an arbitrary state of motion, including accelerated motion. (I stress this because students sometimes think that this result is valid only for inertial motion of the clock.) It makes some physical sense to claim that ‘particles follow a trajectory of least time’ and take the action to be proportional to τ. If we take the proportionality constant as $-mc^2$, we can ensure a suitable limit when $(v/c) \ll 1$: $$ S = -mc^2 \tau$$ $$ = -mc^2 \int dt (1 - v^2(t)/c^2)^{1/2} \quad \to \quad \int dt (1/2 mv^2 -mc^2).$$ So you see, the action for a non-relativistic particle, being an integral over kinetic energy, acquires the nice interpretation of extremizing the proper time, in special relativity, if we ignore the constant $-mc^2$.

This is fine for a free particle but what about a particle in an electromagnetic or a gravitational field? We now have to make sure that any external field we introduce respects special relativity. This limits the kind of expressions we can integrate over to get S. We can only use

$$ S= c_1 \int ds + c_2 \int A_j dx^j + c_3 \int \sqrt{-g_{ij} dx^i dx^j}$$,

up to quadratic order, where the ci-s are constants, Aj is a four-vector and gi j is a second rank tensor. Since $ds = \sqrt{\eta_{ij} dx^i dx^j}$, you can get the first term as a special case of the last by taking $g_{ij} =\eta_{ij}$. So, up to quadratic order, we can only use

$$ S= + c_2 \int A_j dx^j + c_3 \int \sqrt{-g_{ij} dx^i dx^j} $$ with just two external fields: $A_j$ gives you electromagnetism and $g_{ij}$ gives you gravity!

With this structure, it is easy to show that in non-relativistic electrostatics the Lagrangian will turn out to be kinetic energy minus electrostatic potential energy; this is not true in general — even in electromagnetism it is not true when we go beyond electrostatics. The reason we use kinetic energy minus potential energy for gravity is a lot more beautiful. Believe it or not, this is because gravity affects the flow of time!! We will learn this in Chapter 11. chapter 2 in Sleeping Beauties in Theoretical Physics by Thanu Padmanabhan

"On spacetime diagrams, the world line of maximum proper time is the one that looks the shortest. Its a straight line. Curved world lines look longer, but they have smaller proper time. "Time: A Traveler's Guide by Clifford A. Pickover

This is demonstrated nicely at page 54ff in "Emmy Noether's Wonderful Theorem" by Dwight E. Neuenschwander

Moreover:

* Hamilton's principle: why is the integrated difference of kinetic and potential energy minimized? Alberto G. Rojo

• Alternatively this can be understood by considering the path integral formulation of quantum mechanics and quantum field theory. In this formulation a particle goes all possible paths between two fixed points. The classical path is then simply the most probable path, because there the amplitudes add coherently. Formulated differently, the paths with extremal action contribute dominantly to the path integral. This can be seen, for example, by using the method of steepest descend.
• See also: https://physics.stackexchange.com/questions/15899/why-the-principle-of-least-action

Why is the correct path given by the path with minimal action?

The answer can be found through the path integral formulation of quantum mechanics. The thing is that a particle really has some probability to go all possible ways. However, the classical path is the most probable path, because paths close this this path interfere constructively and hence yield a big probability. In contrast, for other paths far aways from the classical path the interference is destructive and hence the probability is tiny. The path with minimal action gives the biggest contribution to the path integral in the classical limit $\hbar \to 0$.

This is explained nicely in Section 3 here.

Are there Problems of the Lagrangian Approach?

Feynman himself stresses that “I don’t know what action is.

However, I must confess my unease with this as a fundamental approach. I have difficulties in formulating my unease, but it has something to do with the generality of the Lagrangian approach, so that little guidance may be provided towards finding the correct theories.

Also the choice of Lagrangian is often not unique, and sometimes rather contrived—even to the extent of undisguised complication. There tends to be a remoteness from actual ‘hands‑on’ understanding, particularly in the case of Lagrangians for fields.

Even the Lagrangian for free Maxwell theory, $\frac{1}{4}F_{ab}F^{ab}$, has no obvious physical significance (this quantity being 1/8 of the difference between the squared lengths of the electric and magnetic field vectors, in 3-dimensional terms. Moreover, the 'Maxwell Lagrangian' does not work as a Lagrangian unless it is expressed in terms of a potential, although the actual value of the potential $A_\mu$ is not a directly observable quantity. In the case of gravity (unlike the case of electromagnetism), the Lagrangian for free Einstein theory vanishes identically when the field equation is satisfied (since $R_{ab}-\frac{1}{2}Rg_{ab}=0$ implies $R=0$). Again, $R$ does not work as a Lagrangian unless it is expressed in terms of quantities (normally the metric components in some coordinate system) that are again not invariantly meaningful. In most situations, the Lagrangian density does not itself seem to have clear physical meaning; moreover, there tend to be many different Lagrangians leading to the same field equations.

Lagrangians for fields are undoubtedly extremely useful as mathematical devices, and they enable us to write down large numbers of suggestions for physical theories. But I remain uneasy about relying upon them too strongly in our searches for improved fundamental physical theories.

page 471 in Road to Reality by R. Penrose

Can every system be described in terms of a Lagrangian?

No!

Long ago, Wigner [18] warned of a ‘facile identification’ of symmetries with conservations principles. Wigner’s point was that not all dynamical systems are amenable to a Lagrangian formulation, in which case Noether’s first theorem does not apply. Indeed, Wigner gave a simple example of a system with time translation symmetry but no corresponding conserved quantity. (The attempt to treat the symmetry conservation connection without reliance on the Lagrangian formalism has led to significant work.20)

http://users.ox.ac.uk/~mert2255/papers/symmetries.pdf

see also the discussion here.

How is a Hamiltonian constructed from a Lagrangian with a Legendre transform

https://physics.stackexchange.com/questions/67765/how-is-a-hamiltonian-constructed-from-a-lagrangian-with-a-legendre-transform/67805#67805

What is the difference between Newtonian and Lagrangian mechanics?

See https://physics.stackexchange.com/questions/8903/what-is-the-difference-between-newtonian-and-lagrangian-mechanics-in-a-nutshell

Why are infinite order Lagrangians called non-local?

see https://physics.stackexchange.com/questions/13624/why-are-infinite-order-lagrangians-called-non-local

What is meant by a local Lagrangian density?

see https://physics.stackexchange.com/questions/95018/what-is-meant-by-a-local-lagrangian-density

History

The principle arose out of successive generalizations of earlier principles:

1. first, as we have already seen, there was Heron’s ‘shortest path’ for reflected light (second century AD),
2. then there was Fermat’s‘ Least Time’ for reflection and refraction (1662),
3. then Leibniz, in 1682, in his Principle of Least Resistance, pooh poohed Fermat’s Principle, for why should light make a choice between optimizing ‘time’ and optimizing ‘distance’? No, argued Leibniz, light takes the easiest path, the one for which the ‘resistance’ is least,
4. finally, Maupertuis,in 1644,extended Leibniz’s principle to cover the motion of light and bodies - he called it the Principle of Least Action.

The Lazy Universe by Coopersmith

• See: http://astro1.panet.utoledo.edu/~ljc/bader1.html