Intuitive

A phase space is a mathematical tool that allows us to grasp important aspects of complicated systems.

Each point of the phase space represents one specific configuration a given system can be in.

The state of a system is recorded in a phase space point through all the location and all the momenta the objects in the system have at a given point in time.

The time evolution of a system can then be represented as a path in phase space.

Try to imagine a 'space' of a large number of dimensions, one dimension for each of the coordinates $x_1, x_2,\ldots$, $p_1, p_2,\ldots$ (Mathematical spaces often have many more than three dimensions.) This space is called phase space (see Fig. 5.10). For n unconstrained particles, this is a space of 6n dimensions (three position coordinates and three momentum coordinates for each particle). The reader may well worry that even for a single particle this is already twice as many dimensions as she or he would normally be used to visualizing! The secret is not to be put off by this. Whereas six dimensions are, indeed, more dimensions than can be readily pictured, it would actually not be of much use to us if we were in fact able to imagine it. For just a room full of molecules, the number of phase-space dimensions might be something like

$$ 100000000000000000000000000 . $$

There is no much hope in trying to obtain an accurate visualization of a space that big! Thus, the trick is not even to try - even in the case of the phase space of a single particle. Just think of some vague kind of three-dimensional (or even just two-dimensional) region. Have another look at Fig. 5. 10. That will do.

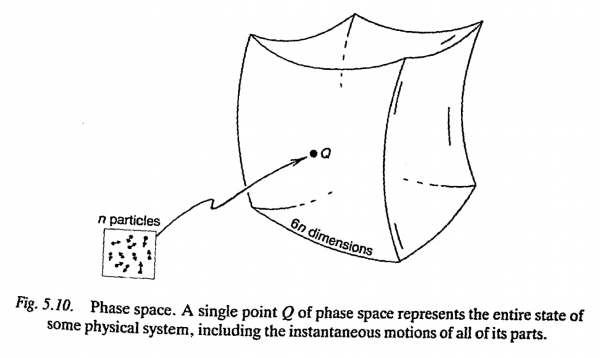
page 174ff in "The Emperors new Mind" by R. Penrose

Concrete

Each point of the phase space corresponds to one particular state of the system.

$\{q_i \}$ defines a point in n-dimensional configuration space $C$. Time evolution is a path in $C$. However, the complete state of the system is defined by $\{q_i \}$ and $\{p_i \}$. Only with this information, we are able to determine the state at all times in the future. The pair $\{q_i, p_i \}$ defines a point in a $2n$-dimensional space we call phase space.

Since each point in phase space is sufficient to determine the time evolution of the system, paths in phase space can never cross. Otherwise, the time-evolution would not be unique.

It is conventional to say that the time evolution is governed by a flow in phase space.

To understand this imagine that you follow one individual trajectory in phase space. Say, you take a pencil, put it down at one point in phase space and then start to draw the correct trajectory for the system which follows from Hamilton's equations. Now, this trajectory is only one thing that can happen in our system. When we are interested in the bigger picture, we need to follow all trajectories that are possible. This means, that we take an infinite number of pencils, put them down and the draw the trajectories. Each trajectory is calculated with Hamilton's equations. The set of all possible trajectories defines a flow in phase space.

Examples

Phase space of a harmonic oscillator

Phase space of a pendlum

Abstract

The space of states in classical mechanics is modeled as a manifold $M$ equipped with a symplectic structure: $(M,ω)$. This manifold is what we usually call phase space. The phase space is a symplectic manifold which simply means that is a manifold equipped with a symplectic structure. A symplectic structure is a distinguished 2-form $(\omega)$.

Such a 2-form is an object that eats two vector fields on our manifold and returns another function on the manifold. Functions on the manifold are smooth maps $f \ : \ M \rightarrow R$. These functions are what we call “the observables of our classical system”. So in words, this means that the observables of our classical system map each state to a real number.

One of the most important function on our phase space manifold is the Hamiltonian function. This function represents the energy of the system and describes the time-evolution of phase space points.

• https://mathoverflow.net/questions/16460/how-to-see-the-phase-space-of-a-physical-system-as-the-cotangent-bundle

In classical mechanics, the phase space is the space of all possible states of a physical system; by “state” we do not simply mean the positions q of all the objects in the system (which would occupy physical space or configuration space), but also their velocities or momenta p (which would occupy momentum space). One needs both the position and momentum of system in order to determine the future behavior of that system. Mathematically, the configuration space might be defined by a manifold M (either finite1 or infinite dimensional), and for each position q ∈ M in that space, the momentum p of the system would take values in the cotangent2 space Tq∗M of that space. Thus phase space is naturally represented here by the cotangent bundle T∗M := {(q,p) : q ∈ M,p ∈ Tq∗M}, which comes with a canonical symplectic form ω := dp ∧ dq.

This may seem surprising; since velocity q ̇ naturally lives in the tangent space TqM, one would expect momentum to also. However, from Lagrangian mechanics, in which the system R evolves by finding formal critical points of a Lagrangian defined as p := ∂L , which lives most naturally in the cotangent space. Dually, the Hamiltonian ∂ q ̇ links momentum to velocity by Hamilton’s equation q ̇ = ∂H . ∂p http://www.math.ucla.edu/~tao/preprints/phase_space.pdf

Why is it interesting?

Hamiltonian Mechanics is geometry in phase space. […]

Mathematical Methods of Classical Mechanics Vladimir Arnold

While it is true that the primary perception we, human beings, have of our world privileges positions, and their evolution with time, this does not mean that we have to use only, mathematics in configuration space. As Basil Hiley puts it “…since thoughts are not located in space-time, mathematics is not necessarily about material things in space- time”. Hiley is right: it is precisely the liberating power — I am tempted to say the grace — of mathematics that allows us to break the chains that tie us to one particular view of our environment." The Principles of Newtonian and Quantum Mechanics: by Gosson

History

See: The tangled tale of phase space by David D. Nolte https://works.bepress.com/ddnolte/2/download/