Add a new page:
 Group theory is the branch of mathematics we use to work with symmetries. A symmetry of an object is a transformation that leaves the object unchanged. The word object is chosen purposefully because it is very vague. There is one branch of mathematics that deals with all kinds of symmetries, any kind of object can have.
Group theory is the branch of mathematics we use to work with symmetries. A symmetry of an object is a transformation that leaves the object unchanged. The word object is chosen purposefully because it is very vague. There is one branch of mathematics that deals with all kinds of symmetries, any kind of object can have.
The most familiar type of symmetries that come to one’s mind are symmetries of geometric shapes, so let's start with that.
A square is defined mathematically as a set of points. A symmetry of the square is a transformation that maps this set of points into itself. This means concretely that by the transformation, no point is mapped to a point outside of the set that defines the square.
Obvious examples of such transformations are rotations, by $90^{\circ}$, $180^{\circ}$, $270^{\circ}$, and of course $0^{\circ}$.
 A counter-example is a rotation by, say $5^{\circ}$. The upper-right corner point $A$ of the square is obviously mapped to a point $A'$ outside of the initial set. Of course, a square still looks like a square after a rotation by $5^\circ$, but, by definition, this is a different square, mathematically a different set of points. Hence, a rotation by $5^{\circ}$ is no symmetry of the square.
A counter-example is a rotation by, say $5^{\circ}$. The upper-right corner point $A$ of the square is obviously mapped to a point $A'$ outside of the initial set. Of course, a square still looks like a square after a rotation by $5^\circ$, but, by definition, this is a different square, mathematically a different set of points. Hence, a rotation by $5^{\circ}$ is no symmetry of the square.
A characteristic property of the symmetries of the square is that the combination of two transformations that leave the square invariant is again a symmetry. For example, combining a rotation by $90^{\circ}$ and $180^{\circ}$ is equivalent to a rotation of $270^{\circ}$, which is again a symmetry of the square. We will elaborate on this in the next post. In fact, the basic axioms of group theory can be derived from such an easy example.
Definition
A group $(G, \circ)$ is a set $G$, together with a binary operation $\circ$ defined on $G$, that satisfies the following axioms
Examples
The first check we have to perform is closure. If we take two elements of $\mathbb{Z}$ and add them, the result should be again an element of $\mathbb{Z}$? Formulated differently: if $a,b \in \mathbb{Z}$, is $a+b\in \mathbb{Z}$? The answer is yes since the sum of two integers is again an integer. Therefore, the closure criterium is fulfilled.
Next, we check if the associativity criterium is fulfilled. Since for $a,b,c \in \mathbb{Z}$, it is true that $a+(b+c) = (a+b)+c$ we can conclude that the criterium is fulfilled.
As a third step we check if there is an identity element. Does an element $e\in \mathbb{Z}$ exist which has the property that when you add to any other integer you get that same integer? The answer is yes since the integer $0$ has this property.
The last quesiton we need to answer is: is there an inverse? Formulated more precisely: Is there for any integer $a\in \mathbb{Z}$ another integer $b\in \mathbb{Z}$ such that $a+b = e = 0$? Again, the answer is yes $a^{-1} = -a$.
Therefore, all criteria are fulfilled an we can conclude that $(G,\star) = (\mathbb{Z},+)$ is a group.
Associativity also holds.
The identity element is again 0.
And also analogously, the inverse element is again $-a$ and also lives in $ \mathbb{R}$.
Associativity also holds.
An identity also exists: We can multiply any real number $a\in \mathbb{R}$ by $1$ and get again $a$.
However, the existence of an inverse element is here a bit trickier. We need to answer the question: Is there for any real number another real number that you can multiply it with to get 1? A first guess is $a^{-1} = {1\over a}$. However this doesn't work because what about $a=0$?
Although this is the only exception we have to conclude that $(\mathbb{R},\cdot)$ is not a group.
However, if we consider the $\mathbb{R} - \{0\}$,, i.e. the real numbers without the zero, instead of $\mathbb{R}$, then we get a group.
This construction yields indeed a group and it is called the Trivial Group.
Recommended Resources
Three books that explain group theory (but do not proof things) with a focus on how it's used in modern physics are
Good books that focus on mathematical aspects (and also include proofs) are:
For Group Theory in Quantum Mechanics see http://math.ucr.edu/home/baez/lie/lie.html
Resources:
There are groups that have nothing to do with symmetries like, for example, braid groups:
„Once we have the notion “group,” we can look for other examples. It turns out there are many examples of groups that have nothing to do with symmetries, which was our motivation to introduce the concept of a group in the first place. This is actually a typical story. The creation of a mathematical concept may be motivated by problems and phenomena in one area of math (or physics, engineering, and so forth), but later it may well turn out to be useful and well adapted to other areas. It turns out that many groups do not come from symmetries“
Love and Math by Frenkel
Group theory is the mathematical theory that we use to describe symmetries. Almost everything in modern physics has its origin in some symmetry consideration and for this reason, group theory is used everywhere in modern physics.
We need a super-mathematics in which the operations are as unknown as the quantities they operate on, and a super-mathematician who does not know what he is doing when he performs these operations. Such a super-mathematics is the Theory of Groups.
Sir Arthur Stanley Eddington
In the 1970’s, high energy physicists pursued Lie algebra theory as a valuable tool to characterize all the gauge interactions. These are now understood to be SU(3) for the strong force (which describes the interacations between quarks, which are the constituents of hadrons such as the proton), and SU(2) × U(1) for both the weak and electromagnetic interactions of quarks and leptons (such as the electron). This is an important feature of the standard model of particle physics [YM,We,Sa,Gl]. Grand unification was an effort to combine these symmetries as subgroups of a unifying group such as SU(5). Superstring unification provides an alternative mechanism to combine symmetries.
The interpretation of fundamental force laws in terms of group theory is now commonly understood in terms of E. Noether’s theorem which identifies the elements of the Lie algebra with the charges conserved in the interactions [No]. The symmetry is used to label the physical states: the eigenvalues of the Cartan subalgebra are the quantum numbers of the elementary particles. The quantum numbers are known as charge, spin, hypercharge, isospin, etc. depending on which group is being considered. Modern high energy theorists effectively think of the elementary particles of the strong, weak and electromagnetic forces as irreducible representations of the direct product of the Poincar´e group and SU(3) × 2 SU(2) × U(1). Selection rules derived from the conserved charges limit allowed transitions of quantum numbers. Explicit solutions of four-dimensional quantum field theory transition amplitudes, however, are known only in a perturbative expansion, i.e. they are not known exactly. This weak coupling perturbative approximation is extremely useful in electroweak theory, but the strong coupling problem of why the quarks are confined inside the hadrons remains more elusive
A man who is tired of group theory is a man who is tired of life. Sidney Coleman
Group theory is, in short, the mathematics of symmetries. You already know that symmetries can be very important in understanding or simplifying physics problems. When you study classical mechanics, you learn that symmetries of a system are intimately related to the existence of conserved charges. Their existence often makes solving for the dynamics a lot simpler. Even if a symmetry is not present exactly (for instance, when a system is almost-but-not-quite spherically symmetric), we can often describe the system as a small perturbation of a system that does exhibit symmetry. A surprisingly large number of physics problems is built around that idea; in fact, practically all systems for which we can solve the dynamics exactly exhibit some sort of symmetry that allow us to reduce the often horrible secondorder equations of motion to much simpler first-order conservation equations.http://maths.dur.ac.uk/users/kasper.peeters/pdf/groups.pdf
An important distinction is between continuous groups and finite groups.
Important Finite Groups
The combination of charge conjugation $C$, parity $P$ and time reversal $T$, called $CPT$ is a fundamental symmetry of nature.
However, each individual symmetry is broken. The discovery that $C$, $P$, $T$, and also the combination $CP$ are broken was one of the biggest surprises in modern physics and there is still no theoretical explanations.
Internal Symmetry Groups
In addition to the discrete groups related to the Poincare group there are many additional groups that are of interested in modern physics.
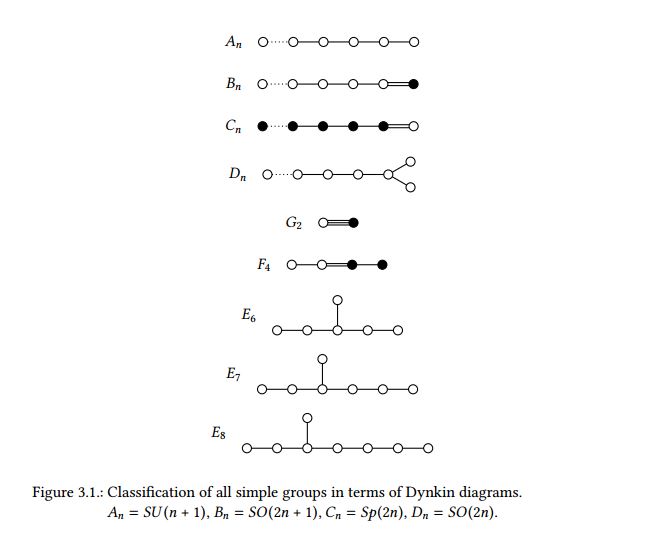
The "atoms" of all groups are called "simple groups" since all other groups can be written as products of these groups.
All simple finite groups are known and a nice essay on the classification of them can be found here. The standard reference is the Atlas of Finite Group by John Horton Conway.
Discrete groups are used in crystallography and also in flavor models that try to solve the flavor puzzle.
Important Continuous Groups
Internal Symmetry Groups
| SO(n) | SU(n) | |||||||||||||||||||||||||||
| ... | ||||||||||||||||||||||||||||
| E8 | SO(18) | |||||||||||||||||||||||||||
| E6 | ||||||||||||||||||||||||||||
| SO(10) | ||||||||||||||||||||||||||||
| Pati-Salam | SU(5) | |||||||||||||||||||||||||||
| SU(3) | ||||||||||||||||||||||||||||
| SU(2) | ||||||||||||||||||||||||||||
| U(1) | ||||||||||||||||||||||||||||
The "atoms" of all groups are the so-called simple groups. Every other group can be written as a product of the simple groups. All simple groups are known and this classification tells us what groups we can use in physics.
On the left-hand side, some of the most important groups that are used in physics are shown. Most of them are important in the context of grand unified theories. The full classification is shown here:
Spacetime Symmetry Groups
| Diffeomorphism Group | ||||||||||||||||||||||||||||
| Conformal Group | ||||||||||||||||||||||||||||
| DeSitter Group | Anti DeSitter Group | |||||||||||||||||||||||||||
| Poincare Group | ||||||||||||||||||||||||||||
| Galilei Group | ||||||||||||||||||||||||||||
For a long time, physicists assumed that the Galilei group is the correct spacetime symmetry group. However, then it was discovered that the speed of light is constant and this meant that instead of the Galilei group, the Poincare group had to be considered.
Nowadays, we know additionally that the cosmological constant is non-zero. This, in turn, means that instead of the Poincare group, we have to use the deSitter group.
A classification of all possible "kinematical" group by deforming the known groups was done in
In addition, the conformal group and the diffeomorphism group are important. These groups cannot be understood as deformations of the other groups. However, all the other groups are subgroups of them.
The diffeomorphism group is the most general spacetime group and consists of all sufficiently smooth transformations. The conformal group is the correct spacetime symmetry group for massless particles.
Important Concepts
The case I have chosen to treat in this paper concerns the question as to whether the group concept should be extended to, or even subsumed by, the groupoid concept. Over a period stretching from at least as long ago as the early nineteenth century, the group concept has emerged as the standard way to measure the degree of invariance of an object under some collection of transformations.4 The informal ideas codified by the group axioms, an axiomatisation which even Lakatos thought unlikely to be challenged, relate to the composition of reversible processes revealing the symmetry of a mathematical entity. Two early manifestations of groups were as the permutations of the roots of a polynomial, later re-interpreted as the automorphisms of the algebraic number field containing its roots, in Galois theory, and as the structure-preserving automorphisms of a geometric space in the Erlanger Programme. Intriguingly, it now appears that there is a challenger on the scene. In some situations, it is argued, groupoids are better suited to extracting the vital symmetries. And yet there has been a perception among their supporters— who include some very illustrious names—of an unwarranted resistance in some quarters to their use, which is only now beginning to decline.The importance of mathematical conceptualisation by David Corfield
To help your intuition further: Lie groups are "almost always" matrix groups as follows. There is a corollary to a difficult theorem known as Ado's theorem that every Lie algebra can be realized as a Lie algebra of square matrices. The same is not true of Lie groups: not every Lie group can be represented as a group of matrices but it is almost true (a consequence of the Peter-Weyl theorem is that every compact group can be realized as a group of square matrices). Certainly, since we can find a square matrix realization for every Lie algebra, we can build a matrix Lie group with that algebra as its Lie algebra through the matrix exponential function; then we find that matrix group's universal cover and this is where we sometimes fail to get a matrix group. This is not typical and the first Lie groups that were not also matrix groups (so called metaplectic groups) weren't found until 1937. These oddballs are all covering groups of noncompact groups.
By exponentiating the Lie algebra elements, which can always can be written as matrices, we get representations of the corresponding universal covering group that belongs to this Lie algebra.
There are two views about symmetry, one of which Michael was expressing. I'll rephrase it as 'symmetry is not fundamental in the structure of physics'. It's just that as you let the renormalization group evolve, you get attracted to fixed points which are often more symmetric than where you started. This particular approach is taken to an extreme by Holga Nielson, who would like to start with nothing, no symmetry principles, not even any logical principles, and somehow get to a fixed point in which everything emerges. My view of this approach is, 'garbage in, beauty out'. I really don't like that point of view.
David Gross in "Conceptual Foundations of Quantum Field Theory" , Edited by Cao
This line of research goes by the name "random dynamics".
What Nielsen imagines is that the whole cosmos is just at the point of a phase transition between two phases. He and his colleagues, such as Don Bennett, try to demonstrate that many of the observed properties of the elementary particles arise simply from this fact, independently of whatever the fundamental laws of physics are. They want to say that, just as bubbles are universally found in liquids that are boiling, the fundamental particles we observe may be simply universal consequences of the universe being balanced at the point of a transition between phases. If so, their properties may to a large extent be independent of whatever fundamental law governs the world.
The Life of the Cosmos by Lee Smolin
His starting point was the theory of algebraic equations (such as the quadratic, or second-degree, equations that children learn in school). In the 1800s, French mathematician Évariste Galois discovered that, in general, equations of higher degree can be solved only partially.
But Galois also showed that solutions to such equations must be linked by symmetry. For example, the solutions to $x^5 = 1$ are five points on a circle when plotted onto a graph comprised of real numbers along one axis and imaginary numbers on the other. He showed that even when such equations cannot be solved, he could still glean a great deal of information about the solutions from studying such symmetries.https://www.nature.com/articles/d41586-018-03423-x