Add a new page:
The Lie group $SU(2)$ describes all possible 3D rotations of a spinorial object, that is, an object that needs to be rotated 720 degrees before returning to its initial state. A good example for such an object is a cube that is attached to a wall by belts: see the animations here https://en.wikipedia.org/wiki/Spinor. In physics, an important spinorial object is the fermion (e.g., an electron).
For small rotations $SU(2)$ is identical to $SO(3)$, that is, both groups have the same Lie algebra.
Every $SU(2)$ transformation can be written as $$ g(x) = a_0(x) 1 + i a_i(x) \sigma ,$$ where $\sigma$ are the Pauli matrices. The defining conditions of $SU(2)$ are $g(x)^\dagger g(x)=1$ and $det(g(x)=1$, and thus we have $$ (a_0)^2 +a_i^2=1 , $$ which is the defining condition of $S^3$.
Source: page 23 in http://www.iop.vast.ac.vn/theor/conferences/vsop/18/files/QFT-4.pdf
This is also shown nicely at page 164 in the book Magnetic Monopoles by Shnir.
Elements of $SU(2)$ can be written as
$$ U(x) = e^{i a \vec{r} \vec{\sigma} } = \cos(a) + i \vec{r} \vec{\sigma} \sin( a )$$
where $\vec{\sigma}=(\sigma_1,\sigma_2,\sigma_3)$ are the usual Pauli matrices and $ \vec{r} $ is a unit vector. This is also known as the version of the the well-known Euler's identity for $2\times2$ matrices.
Representations
The diagram below shows the defining (2-dimensional) representation of $SU(2)$ in its upper branch and a 3-dimensional representations of the same group in the lower branch. An important application of these two representations is the rotation of the quantum state of a spin-1/2 and a spin-1 particle, respectively. For a more detailed explanation of this diagram and more representations of $SU(2)$ see Fun with Symmetry.
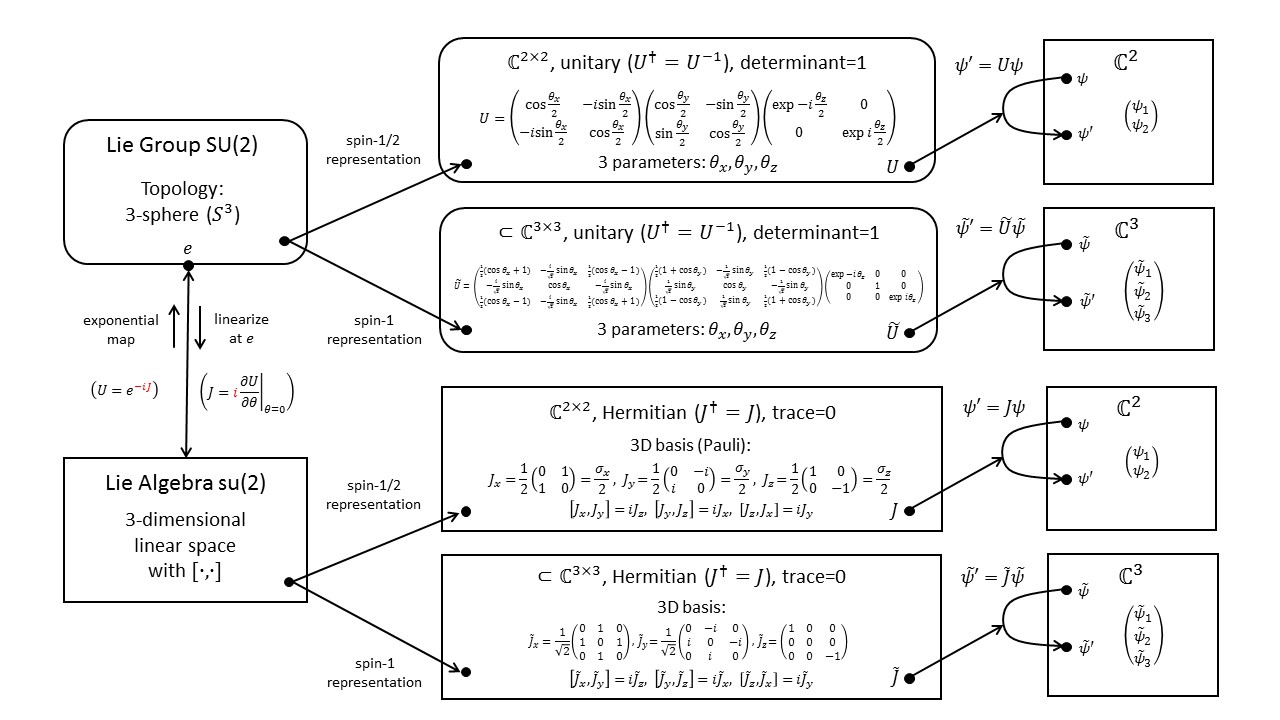
$SU(2)$ is one of the most important groups in modern physics. The group is a crucial ingredient of the gauge symmetry of the standard model of particle physics and, in some sense, explains the structure of weak interactions.
In addition, the fundamental spacetime symmetry group called Lorentz group, is usually analyzed in terms of its Lie algebra. This Lie algebra can be understood as two copies of the $SU(2)$ Lie algebra. Hence, by understanding the Lie algebra of $SU(2)$, we understand almost everything about the Lorentz group. This analysis is crucial for the understanding what spin is, which is one of the most important properties of elementary particles.