Intuitive

The Maxwell equations tell us that electric charge never gets lost but is always conserved. In addition, they tell us how charged objects interact with each other.

There are in total 4 Maxwell equations and each tells us something important about electricity, magnetism and their interplay.

• Gauss' Law describes how an electric field originates from an electric charge.
• Gauss' Law of magnetism describes the magnetic field.
• Faraday's Law tells us to how a changing magnetic field creates an electric field
• Ampere's Law tells us how a current can be induced by a moving magnet (= a generator) and equally how a magnetic field can be induced by a current (= a motor, electromagnet).

Concrete

The conventional form of the Maxwell equations that, for example, engineers use is

$$\quad \partial_t \vec{E} + \nabla \times \vec{B} = \vec J, \ \nabla \vec{E} = J^0 \equiv \rho, \ \nabla \vec B = 0, \ \nabla \times \vec E + \partial_t \vec B = 0 . $$

Example: Electric field of an infinitely long, straight wire

We consider a cylinder of length $L$ and radius $\rho$, which is centered around the $\hat{z}$ axis. The charge in the cylinder is $Q=L\,\lambda$ and the surface area of its mantel is $A=2\pi\,\rho\,L$. By symmetry reasons Gauss's law gives then $$ E(\rho)\,2\,\pi\,\rho\,L = 4\pi\,Q = 4\pi\,L\,\lambda\ \Rightarrow\ E(\rho) = 2\,\frac{\lambda}{\rho} $$ and as vector $$ \vec{E}=E(\rho)\,\hat{\rho}=2\,\frac{\lambda}{\rho}\,\hat{\rho}\ .$$

Conservation of Charge

An important consequence of the Maxwell equations is that charge is conserved. To see this we consider the inhomogeneous Maxwell equation

$$ \partial_t \vec{E} + \nabla \times \vec{B} = \vec J$$ and take the divergence of both sides: \begin{eqnarray} \boldsymbol{\nabla} \times \vec B - {\partial \vec E \over \partial t} = \vec J &\Longrightarrow & \boldsymbol{\nabla} \cdot \boldsymbol{\nabla}\times \vec B - {\partial \over \partial t} \boldsymbol{\nabla} \cdot \vec E = \boldsymbol{\nabla} \cdot \vec J \\ &\Longrightarrow & \boldsymbol{\nabla} \cdot \vec J +{\partial \rho \over \partial t} = 0. \end{eqnarray} To get to the last line, we used the other Maxwell equation $\vec{E} = J^0= \rho$ and that the divergence of a curl always vanishes.

This equation is a conservation equation and tells us that charge is conserved.

• A great discussion can be found in A student's guide to Maxwell's equations by Daniel A. Fleisch.
• See also http://physics.stackexchange.com/questions/3005/derivation-of-maxwells-equations-from-field-tensor-lagrangian?rq=1 and
• http://www.staff.science.uu.nl/~wit00103/ftip/Ch04.pdf

The static limit of Maxwell's equations is known as Coulomb's law.

Relationship to Lorentz and U(1) Gauge Symmetry

The diagram below maps the path from Lorentz symmetry and U(1) gauge symmetry to the Maxwell equations. For a detailed explanation see Fun with Symmetry.

Abstract

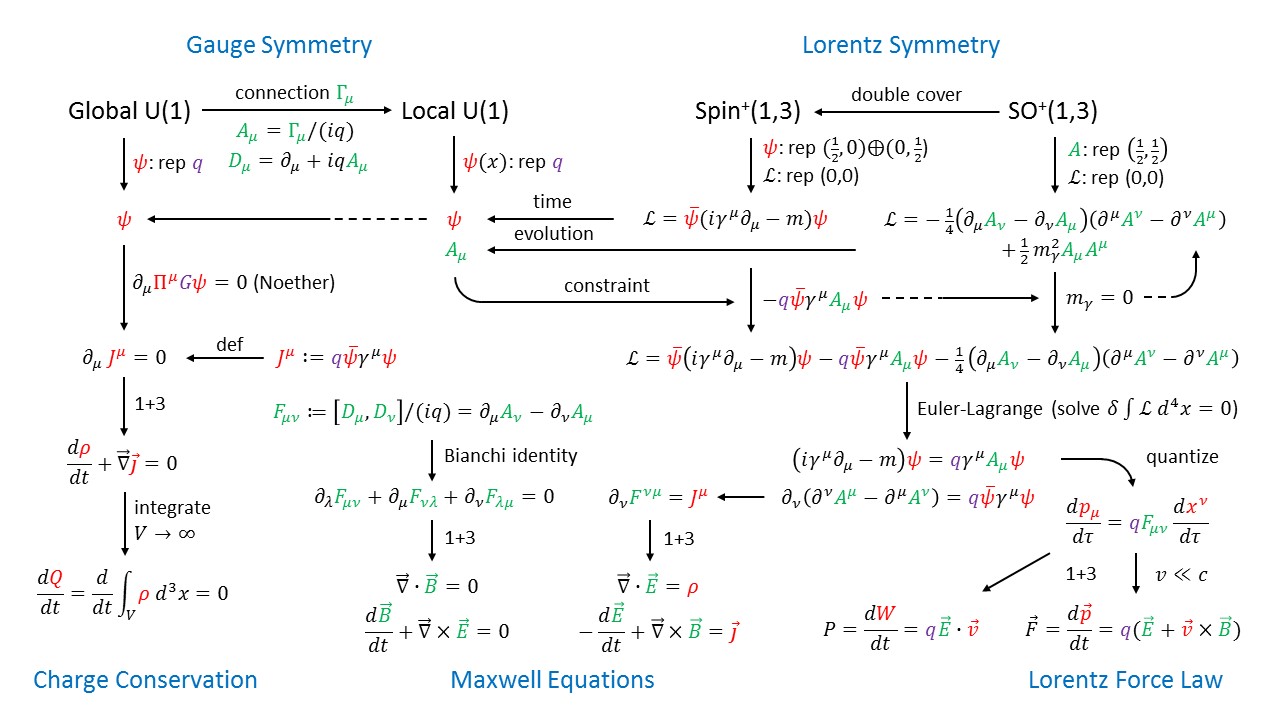
The Maxwell equation can be written more compactly with the help of the field strength tensor and its dual

$$ \partial_\sigma F^{ \sigma \rho} = J^\rho, \quad \partial_\mu \tilde{ F}^{ \mu \nu} =0 $$

Relationship between the field-strength tensor, potentials and fields

\begin{eqnarray} F^{\mu \nu} \equiv \partial^{\mu}A^{\nu} - \partial^{\nu}A^{\mu} = \begin{pmatrix} 0 & -E_x & -E_y & -E_z \\ E_x & 0 & -B_z & B_y \\ E_y & B_z & 0 & -B_x \\ E_z & -B_y & B_x & 0 \end{pmatrix} \end{eqnarray}

\begin{eqnarray} \vec E &=& - {\partial \vec A \over \partial t} - \boldsymbol{\nabla} \phi \\ \vec B &=& \boldsymbol{\nabla} \times \vec A \label{eq:eandbfieldsdefinedintermsofscalarandvectorpotentials} \end{eqnarray}

This can also be inverted:

\begin{equation} \label{eq:E-fielddef} \partial^i A^0 - \partial^0 A^i \equiv E^i \end{equation} \begin{equation} \epsilon^{ijk}\partial^j A^k \equiv - B^i \end{equation} and therefore \begin{equation} \label{eq:E-fielddef2} F^{i 0} = E^i \end{equation} \begin{equation} \label{eq:defBfeld} F^{ij} = \epsilon^{ijk} \epsilon^{klm} \partial^l A^m = - \epsilon^{ijk} B^k \, . \end{equation}

and in addition, the dual field-strength tensor is defined

$$ \tilde{ F}^{ \mu \nu} = \epsilon^{\mu \nu \rho \sigma } F^{ \rho \sigma} $$

Maxwell's equation in terms of differential forms

The statement $d* J=0 $ or in a more familiar notation $\nabla \times J =0$ encodes the automatic conservation of source.

(Source: page 370 in Gravitation by Misner, Thorne, Wheeler)

As already indicated in the diagram above, Maxwell's equations can be written extremely compactly with the help of differential forms: \begin{eqnarray} d\star \bf F\it_{(2)} &= \star \bf J\it_{(1)} \\ d \bf F\it_{(2)} &= 0 \end{eqnarray}

To understand this, we start with the $1$-form \begin{eqnarray} \bf A\it_{(1)} = A_{\mu} dx^{\mu} \end{eqnarray} The we take the exterior derivative of this: \begin{eqnarray} d \bf A\it_{(1)} &=& \partial_{\mu} A_{\nu} dx^{\mu} \wedge dx^{\nu} \\ &=& {1 \over 2} (\partial_{\mu}A_{\nu} - \partial_{\nu}A_{\mu}) dx^{\mu} \wedge dx^{\nu} \\ &\equiv& {1 \over 2} F_{\mu \nu} dx^{\mu} \wedge dx^{\nu} \label{eq:firststatementofexteriorderivofAtogetFmunu} \end{eqnarray} where we have defined the two form \begin{eqnarray} \bf F\it_{(2)} = F_{\mu \nu} dx^{\mu} \wedge dx^{\nu} . \end{eqnarray} This two-form is, of course, the antisymmetric field-strength tensor.

This formulation is identical to usual one, where $\bf A\it_{(1)}$ is the potential and $\bf F\it_{(2)}$ is the field strength, with \begin{eqnarray} F_{\mu\nu} = \partial_{\mu} A_{\nu} - \partial_{\nu} A_{\mu} \end{eqnarray}

Since the exterior derivative is nilpotent, we have \begin{eqnarray} d \bf F\it_{(2)} = d (d\bf A\it_{(1)}) = d^2 \bf A\it_{(1)} \equiv 0 \end{eqnarray} In components this reads \begin{eqnarray} d \bf F\it_{(2)} &=& \partial_{\mu} F_{\nu \lambda} dx^{\mu}\wedge dx^{\nu} \wedge dx^{\lambda} \\ &=& {1 \over 3} (\partial_{\mu} F_{\nu \lambda} + \partial_{\nu} F_{\lambda \mu} + \partial_{\lambda} F_{\mu \nu}) dx^{\mu} \wedge dx^{\nu} \wedge dx^{\lambda} \\ &=& 0 \end{eqnarray} which are exactly the homogeneous Maxwell equations.

To write down the inhomogeneous Maxwell equation using differential forms, we need to Hodge star operator. Otherwise, we can't write down an equation with a derivative, since, as shown, above, it always vanishes.

Taking the Hodge star of $\bf F\it_{(2)}$ yields \begin{eqnarray} \star \bf F\it_{(2)} &=& \star F_{\mu \nu} dx^{\mu} \wedge dx^{\nu} \\ &=& {1 \over 2!(4-2)!} F_{\mu \nu} \epsilon^{\mu \nu}_{\lambda \sigma} dx^{\lambda} \wedge dx^{\sigma} \\ &=& {1 \over 4} F_{\mu \nu} \eta_{\lambda\tau} \eta_{\sigma\upsilon} \epsilon^{\mu \nu \tau \upsilon} dx^{\lambda} \wedge dx^{\sigma} \\ &=& E_1 dx^2 \wedge dx^3 + E_2 dx^3 \wedge dx^1 + E_3 dx^1 \wedge dx^2 \\ & & -B_1 dx^1 \wedge dx^0 - B_2 dx^2 \wedge dx^0 - B_3 dx^3 \wedge dx^0 \label{eq:starFinformnotation} \end{eqnarray}

Now, we can take the exterior derivative and get something that does not vanish: \begin{eqnarray} d\star \bf F\it_{(2)} &=& \partial_1 E_1 dx^1 \wedge dx^2 \wedge dx^3 + \partial_0 E_1 dx^0 \wedge dx^2 \wedge dx^3 \\ & & + \partial_2 E_2 dx^2 \wedge dx^3 \wedge dx^1 + \partial_0 E_2 dx^0 \wedge dx^3 \wedge dx^1 \\ & & + \partial_3E_3 dx^3 \wedge dx^1 \wedge dx^2 + \partial_0 E_3 dx^0 \wedge dx^1 \wedge dx^2 \\ & & -\partial_2 B_1 dx^2 \wedge dx^1 \wedge dx^0 - \partial_3 B_1 dx^3 \wedge dx^1 \wedge dx^0 \\ & & -\partial_1B_2 dx^1 \wedge dx^2 \wedge dx^0 - \partial_3 B_2 dx^3 \wedge dx^2 \wedge dx^0 \\ & & - \partial_1 B_3 dx^1 \wedge dx^3 \wedge dx^0 - \partial_2 B_3 dx^2 \wedge dx^3 \wedge dx^0 \\ &=& (\partial_1E_1 + \partial_2 E_2 + \partial_3E_3) dx^1 \wedge dx^2 \wedge dx^3 \\ & & + (\partial_0 E_3 + \partial_2 B_1 - \partial_1B_2) dx^0 \wedge dx^1 \wedge dx^2 \\ & & +(\partial_0E_2+ \partial_1B_3 - \partial_3B_1)dx^0 \wedge dx^3 \wedge dx^1 \\ & & +(\partial_0 E_1 + \partial_3B_2 - \partial_2B_3)dx^0 \wedge dx^2 \wedge dx^3 . \end{eqnarray}

When we now compare this to the Maxwell equations in the usual notation, we see that if we define \begin{eqnarray} \bf J\it_{(1)} = \rho dx^0 + J_1 dx^1 + J_2dx^2+J_3dx^3 \end{eqnarray} then \begin{eqnarray} \star \bf J\it_{(1)} &=& \rho dx^1 \wedge dx^2 \wedge dx^3 + J_1 dx^0 \wedge dx^2 \wedge dx^3 \\ & & J_2 dx^0 \wedge dx^3 \wedge dx^1 + J_3 dx^0 \wedge dx^1 \wedge dx^2 . \end{eqnarray} Therefore, the equations \begin{eqnarray} d\star \bf F\it_{(2)} = \star \bf J\it_{(1)} \label{eq:formversionofinhomogmaxwell} \end{eqnarray} are eactly the inhomogeneous Maxwell equations.

See also

• A pictorial introduction to differential geometry, leading to Maxwell's equations as three pictures by Jonathan Gratus

Why is it interesting?

Maxwell's equations are an elegant and concise way to lay out the fundamentals of electricity and magnetism.

Maxwell's equations wholly define the evolution of the electromagnetic field. So, given a full specification of an electromagnetic system's boundary conditions and constitutive relationships (i.e. the data defining the materials within the system by specifying the relationships between the electric / magnetic field and electric displacement / magnetic induction), they let us calculate the electromagnetic field at all points within the system at any time. Experimentally, we observe that knowledge of the electromagnetic field together with the Lorentz force law is all one needs to know to fully understand how electric charge and magnetic dipoles (e.g. precession of a neutron) will react to the World around it. That is, Maxwell's equations + boundary conditions + constitutive relations tell us everything that can be experimentally measured about electromagnetic effects

https://physics.stackexchange.com/questions/322598/what-is-special-about-maxwells-equations/322610#322610

Derivation

Derivation of the inhomogeneous Maxwell equations

The Maxwell equations can be derived from the Lagrangian

$$ \mathcal{L}_{EM} = -{1\over 4} F_{\mu \nu}F^{\mu \nu} - J^{\mu}A_{\mu} .$$

The corresponsing action is therefore \begin{eqnarray} S = \int d^4x \bigg[-{1\over 4}F_{\mu \nu}F^{\mu \nu} - J^{\mu}A_{\mu}\bigg] \label{eq:emaction} \end{eqnarray}

Now we take the variation of this action with respect to $A^{\mu}$: \begin{eqnarray} \delta S &=&\int d^4x \bigg[-{1\over 4}F_{\mu \nu} \delta F^{\mu \nu} - {1\over 4} \delta F_{\mu \nu}F^{\mu \nu} - J^{\mu} \delta A_{\mu} \bigg] \\ &=& \int d^4x \bigg[-{1\over 2}F_{\mu \nu}\delta F^{\mu \nu} - J^{\mu} \delta A_{\mu}\bigg] \\ &=&\int d^4x \bigg[-{1\over 2}F_{\mu \nu}(\partial^{\mu}\delta A^{\nu} - \partial^{\nu}\delta A^{\mu}) - J^{\mu}\delta A_{\mu}\bigg] \\ &=&\int d^4x \bigg[-F_{\mu \nu} \partial^{\mu} \delta A^{\nu} - J^{\mu}\delta A_{\mu}\bigg] \end{eqnarray} Now we integrate the first term by parts and choose boundary conditions such that $\delta A$ vanishes at the boundaries. This yields \begin{eqnarray} &=& \int d^4x \bigg[\partial_{\mu}F^{\mu \nu}\delta A_{\nu} - J^{\nu}\delta A_{\nu}\bigg] \\ &=& \int d^4x \bigg[\partial_{\mu}F^{\mu \nu} - J^{\nu}\bigg] \delta A_{\nu} \end{eqnarray} Thereofore, the correct configuration which extremize the action ($\delta S = 0$), are those that fulfil $\partial_{\mu}F^{\mu \nu} = J^{\nu}$.

These are exactly the inhomogenous Maxwell equations.

Derivation of the homogeneous Maxwell equations

It follows directly from way we define the electromagnetic tensor $F_{ \mu \nu}$ that if we multiply it with something totally antisymmetric: \begin{equation} \tilde{ F}^{ \mu \nu} = \epsilon^{\mu \nu \rho \sigma } F^{ \rho \sigma} \end{equation} the derivative $\partial_\mu$ of this new object $\tilde{ F}^{ \mu \nu} $ vanishes:

\begin{equation} \partial_\mu \tilde{ F}^{ \mu \nu} = \partial_\mu \epsilon^{\mu \nu \rho \sigma } ( \partial_\sigma A_\rho - \partial_\rho A_\sigma) =0. \end{equation}

The combination of the field strength tensor with antisymmetric Levi-Civita symbol is known as dual field strength tensor.

Let's show this explicitly for the first term:

\begin{align} \epsilon^{\mu \nu \rho \sigma } \partial_\mu \partial_\sigma A_\rho &= \frac{1}{2} ( \epsilon^{\mu \nu \rho \sigma } \partial_\mu \partial_\sigma A_\rho + \epsilon^{\mu \nu \rho \sigma } \partial_\mu \partial_\sigma A_\rho ) \notag \\ &\underbrace{=}_{{\text{Renaming dummy indices}}} \frac{1}{2} ( \epsilon^{\mu \nu \rho \sigma } \partial_\mu \partial_\sigma A_\rho + \epsilon^{\sigma \nu \rho \mu } \partial_\sigma \partial_\mu A_\rho ) \notag \\ &\underbrace{=}_{{\text{Because } \epsilon^{\mu \nu \rho \sigma} = - \epsilon^{\sigma \nu \rho \mu} \text{ and } \partial_\mu \partial_\sigma = \partial_\sigma \partial_\mu } }\frac{1}{2} ( \epsilon^{\mu \nu \rho \sigma } \partial_\mu \partial_\sigma A_\rho - \epsilon^{\mu \nu \rho \sigma } \partial_\mu \partial_\sigma A_\rho ) = 0 \qquad \checkmark \end{align} Equally we can calculate that the second term is zero.

The equations \begin{equation} \partial_\mu \tilde{ F}^{ \mu \nu} = 0 \end{equation}

from above are exactly the homogeneous Maxwell equations.

Derivation

• For a derivation of Maxwell's equations using group theory, see From Quantum Mechanics to Maxwell’s Equations Daniel J. Cross
• For an elementary derivation of the Maxwell equations, see Physics from Symmetry by Schwichtenberg

Interpretation

The Maxwell equation describe the conservation of magnetic flux and electric charge

The homogeneous Maxwell equations $$\partial_\mu \tilde{ F}^{ \mu \nu} =0$$ or equivalently $$ \nabla \vec B = 0, \quad \nabla \times \vec E + \partial_t \vec B = 0 , $$ encode the conservation of magnetic flux. This interpretation comes about since the equation $\partial_\mu \tilde{ F}^{ \mu \nu} =0$ describes a conserved current for each index $\nu$. When we have a conserved current, we automatically have a conserved charge. In this case the conserved charge is the magnetic flux.

The inhomogeneous Maxwell equations

$$\partial_\sigma F^{ \sigma \rho} = J^\rho $$ or equivalently

$$\partial_t \vec{E} + \nabla \times \vec{B} = \vec J, \quad \ \nabla \vec{E} = J^0 \equiv \rho $$

encode the conservation of electric charge. (Source)

The foundations of electrodynamics have nothing to do with special relativity and the Poincare group, they are rather of a generally covariant (“topological”) nature based on the conservation laws of electric charge and magnetic flux. https://arxiv.org/pdf/gr-qc/0506042.pdf

The Maxwell equations tell us which degrees of freedom are non-physical

A massless spin 1 particle has 2 degrees of freedom. However, we usually describe it using four-vectors, which have four components. Hence, somehow we must get rid of the superfluous degrees of freedom. The superfluous freedom in theory is usually called gauge symmetry.

This job is done by the Maxwell equations.

In some sense, Maxwell’s equations were a historical accident. Had the discovery of quantum mechanics preceded the unification of electricity and magnetism, Maxwell’s equations might not have loomed so large in the history of physics. In the quantum description of the electromagnetic field, photons are the fundamental building blocks. Photons are described by a four-vector k that obeys k · k = 0 in free space, and a helicity index indicating a projection of an angular momentum ±1 along the direction of propagation of the photon. Every physical state is described by a superposition of the photon basis states, and every superposition describes a possible physical state. In this description of the electromagnetic field in free space no constraint equations are necessary. The nineteenth century description of the electromagnetic field proceeds along somewhat different lines. A multicomponent field (E,B) is introduced at each point in space-time. The components of the field transform in a very elegant way under homogeneous Lorentz transformations (as a tensor). If the field is Fourier transformed from the coordinate to the momentum representation, then each four-momentum has six components associated with it. These are the components of a second order antisymmetric tensor. Since the quantum description has only two independent components associated with each four-momentum, there are four dimensions worth of linear combinations of the classical field components that do not describe physically allowed states, for each four-momentum. Some mechanism must be derived for annihilating these superpositions. This mechanism is the set of equations discovered by Maxwell. In this sense, Maxwell’s equations are an expression of our ignorance. It is ironic that the first truly powerful applications of group theory were to the solutions of equations. We now understand that group theory, by pointing to the appropriate Hilbert space for the electromagnetic field, allows us to relate physical states to arbitrary superpositions of basis states. Since no superpositions are forbidden, no equations are necessary. page 273 in Lie Groups, Physics, and Geometry by Gilmore

A simpler but longer description of the same line of thought

Fields in physics are something which associate with each point in space and with each instance in time a quantity. In case of electromagnetism this is a quantity describing the electric and magnetic properties at this point. Each of these two properties turn out to have a strength and a direction. Thus the electric and magnetic fields associate with each point in space and time an electric and a magnetic magnitude and a direction. For a magnetic field this is well known from daily experience. Go around with a compass. As you move, the magnetic needle will arrange itself in response to the geomagnetic field. Thus, this demonstrates that there is a direction involved with magnetism. That there is also a strength involved you can see when moving two magnets closer and closer together. How much they pull at each other depends on where they are relative to each other. Thus there is also a magnitude associated with each point. The same actually applies to electric fields, but this is not as directly testable with common elements. Ok, so it is now clear that electric and magnetic fields have a direction and a magnitude. Thus, at each point in space and time six numbers are needed to describe them: two magnitudes and two angles each to determine a direction.

When in the 19th century people tried to understand how electromagnetism works they also figured this out. However, they made also another intriguing discovery. When writing down the laws which govern electromagnetism, it turns out that electric and magnetic fields are intimately linked, and that they are just two sides of the same coin. That is the reason to call it electromagnetism.

In the early 20th century it then became clear that both phenomena can be associated with a single particle, the photon. But then it was found that to characterize a photon only two numbers at each point in space and time are necessary. This implies that between the six numbers characterizing electric and magnetic fields relations exist. These are known as Maxwell equations in classical physics, or as quantum Maxwell dynamics in the quantum theory. If you would add, e. g., electrons to this theory, you would end up with quantum electro dynamics - QED.

http://axelmaas.blogspot.de/2010/10/electromagnetism-photons-and-symmetry.html

For a particularly nice visual interpretation see A pictorial introduction to differential geometry, leading to Maxwell's equations as three pictures by Jonathan Gratus

History

• The Long Road to Maxwell’s Equations How four enthusiasts helped bring the theory of electromagnetism to light by James C. Rautio
• For a nice write-up of the experiments and lines of thoughts that led to the Maxwell equations see the corresponding chapter in the book Theoretical concepts in physics by Malcolm Longair.