Intuitive

Quantum electrodynamics is the correct model of electromagnetic interactions. It is a model in the framework of quantum field theory.

• The best non-technical introduction to quantum electrodynamics is Quantum Electrodynamics by Richard P. Feynman

Concrete

Quantum electrodynamics is a quantum field theory of electrodynamics. At its heart is a gauge symmetry called local $U(1)$ symmetry.

In practice, we use quantum electrodynamics to describe electrodynamical interactions between charged particles through elementary particles called photons.

Photons are the fundamental excitations of the electrodynamic field.

There are two frameworks to calculate things in quantum electrodynamics: either using Feynman diagrams (= the Hamiltonian framework) or using path integrals (= the Lagrangian framework).

See also https://en.wikipedia.org/wiki/Quantum_electrodynamics#Mathematics

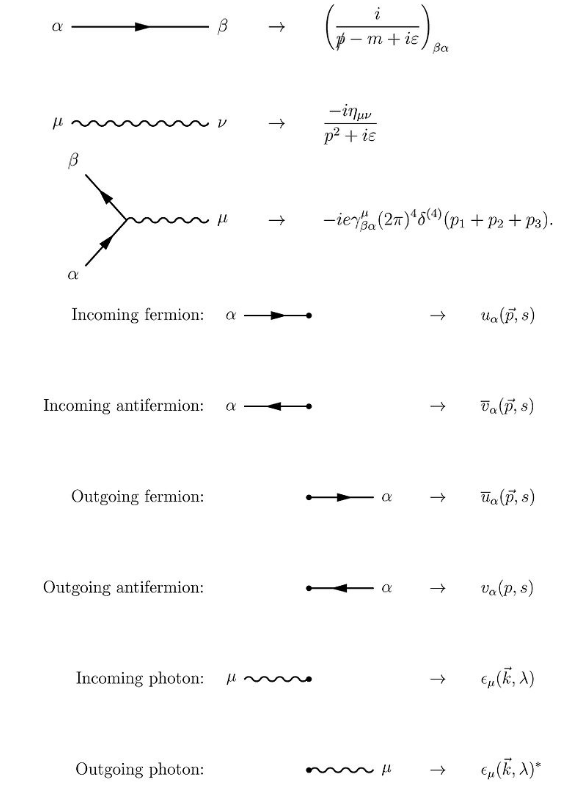
The best resource for the correct Feynman rules of QED is A resource for signs and Feynman diagrams of the Standard Model by Jorge C. Romao. The thing is that there are many different conventions and these authors develop a notation that allows us to map them all onto each other.

The QED Feynman Rules at one Glance

Source: Peskin, Michael; Schroeder, Daniel (1995). An introduction to quantum field theory

Recommended Resources

• Lectures on QED and QCD by Andrey Grozin

Abstract

Additional Conserved Charge

In addition, to the usual electrical charge, which is conserved due to the global $U(1)$ symmetry, there is an additional topological charge.

This follows from the homogeneous Maxwell equations

$$ \partial_\mu \tilde{F}^{\mu \nu} =0 $$

which follow "trivially" from the definition of the dual field strength tensor $\tilde{F}^{\mu \nu} = \epsilon^{\mu \nu \sigma \rho} F_{\sigma \rho}. $ (They are simply the Bianchi idenities.)

They homogeneous Maxwell equations express a conserved current equation for each component $\nu$. For example, for $\nu=1$, we have

$$ \partial_\mu \tilde{F}^{\mu 1} =0 \quad \leftrightarrow \quad \partial_\mu j^\mu =0 ,$$

where I have defined $j^\mu \equiv \tilde{F}^{\mu 1} $.

When we have a conserved current, we have a conserved charge thanks to Gauss' theorem:

$$ Q \equiv \int_V dx^3 j^0 \quad \text{ with} \quad \partial_0 Q =0 .$$

This charge generates an additional global symmetry.

The conserved charge is the magnetic flux associated to the U(1) gauge symmetry.David Tong page 169

Formulated differently:

[It] measures the magnetic flux of a line operator $H(C)$ (the "`t Hooft line operator") which is supported on a line $C$ which links the $S^2$. It corresponds to the worldline of a probe magnetic monopole, and $Q$ measures the magnetic flux of the monopole in the same way that $\int_{S^2} \star F$ measures the electric flux on the worldline of an electric charge. These are called 1-form global symmetries, because the charged operators are supported on lines.

The same story goes through in any dimension $d>2$. We obtain a $(d-3)$-form global symmetry, meaning the charged operators are supported on $(d-3)$-manifolds which link a 2-sphere over which we measure the charge $\int_{S^2} F$.

In 3 dimensions, $j=\star F$ is a 1-form, so this is an ordinary global symmetry. The 't Hooft operators are pointlike magnetic monopole operators, whose charge is again the magnetic flux.https://physics.stackexchange.com/a/391273/37286

Recommended Resources

• https://ncatlab.org/nlab/show/quantum+electrodynamics

Experimental Tests

• A great review of experimental tests of QED can be found here.
• Savely G. Karshenboim, D. I. Mendeleev, The Lamb Shift of Hydrogen and Low-Energy Tests of QED

Why is it interesting?

Quantum electrodynamics (QED) is the best theory of electromagnetic interactions that we have.

It's a crucial part of the standard model and accurately describes how elementary particles like electrons interact with each other and with light.

In addition, it's one of the best-tested theories in the history of science and so far, passed all precision tests.

Electromagnetic interactions are responsible for the attraction between electrons and protons. This way they are responsible for the stability of atoms.

History

• "QED and the Men Who Made It: Dyson, Feynman, Schwinger, and Tomonaga" by Schweber
• The notion “quantum electrodynamics” was invented by Paul Dirac in The quantum theory of emission and absorption of radiation