Intuitive

When an object is at rest it has no momentum. When it has a lot of momentum it changes its location quickly. Hence there is a connection between momentum and the change of location. Similarly, if an object doesn't rotate it has no angular momentum. Hence there is a connection between rotations and angular momentum. In a similar spirit we can say that an object that does not change at all over time has no energy.

In a somewhat more formal way we say that momentum generates translations (= changes of the position), angular momentum generates rotations and energy generates temporal translations (= movements forward in time). Momentum is responsible that an object changes its location, angular momentum that it rotates and energy that it changes as time passes on.

Noether's theorem tells us that there is also a connection the other way round. Namely starting from the transformations: change of location, rotations and movements forward in time; we can derive the quantities; momentum, angular momentum and energy.

Whenever we have a physical system, we can transform this system and if the transformed system is indistinguishable from the original one, the transformation we performed is a symmetry. So, for example, if we rotate our system and it is indistinguishable to the unrotated system, we say it has rotational symmetry.

• Now, Noether's theorem tells us that whenever a system is rotational symmetric there is a conserved quantity that we can recognize as the usual angular momentum.
• Similarly, if a system does not change under translations we get a conserved quantity that looks exactly like the quantity we call momentum.
• And if a system does not change as time passes on its energy is conserved.

If we assume that the laws of physics are describable by a minimum principle, then we can show that if a law is such that you can move all the equipment to one side, in other words if it is translatable in space, then there must be conservation of momentum. There is a deep connection between the symmetry principles and the conservation laws, but that connection requires that the minimum principle be assumed. In the second lecture we discussed one way of describing physical laws by saying that a particle goes from one place to another in a given length of time by trying different paths. There is a certain quantity which, perhaps misleadingly, happens to be called the action. When you calculate the action on the various paths you will find that for the actual path taken this quantity is always smaller than for any other. That way of describing the laws of nature is to say that the action of certain mathematical formulae is least for the actual path of all the possible paths. Another way of saying a thing is least is to say that if you move the path a little bit at first it does not make any difference. Suppose you were walking around on hills – but smooth hills, since the mathematical things involved correspond to smooth things – and you come to a place where you are lowest, then I say that if you take a small step forward you will not change your height. When you are at the lowest or at the highest point, a step does not make any difference in the altitude in first approximation, whereas if you are on a slope you can walk down the slope with a step and then if you take the step in the opposite direction you walk up. That is the key to the reason why, when you are at the lowest place, taking a step does not make much difference, because if it did make any difference then if you took a step in the opposite direction you would go down. Since this is the lowest point and you cannot go down, your first approximation is that the step does not make any difference. We therefore know that if we move a path a little bit it does not make any difference to the action on a first approximation.

We draw a path, A to B (fig. 25), ), and now I want you to consider the following possible other path. First we jump immediately over to another place near by, C, then we move on exactly the corresponding path to another point, which we will call D, which is displaced the same amount, of course, because it is the corresponding path. Now we have just discovered that the laws of nature are such that the total amount of action going on the ACDB path is the same in the first approximation to that original path AB – that is from the minimum principle, when it is the real motion. I will tell you something else. The action on the original path, A to B, is the same as the action from C to D if the world is the same when you move everything over, because the difference of these two is only that you have moved everything over. So if the symmetry principle of translation in space is right, then the action on the direct path between A and B is the same as that on the direct path between C and D. However for the true motion the total action on the indirect path ACDB is very nearly the same as on the direct path AB, and therefore the same as just the part C to D. This indirect action is the sum of three parts – the action going A to C, that of C to D, plus that from D to B. So, subtracting equals from equals, you can probably see that the contribution from A to C and that from D to B must add up to zero. But in the motion for one of these sections we are going one way, and for the other the opposite way. If we take the contribution of A to C, thinking of it as an effect of moving one way, and the contribution of D to B as B to D, taking the opposite sign because it is the other way, we see that there is a quantity A to C which has to match the quantity B to D to cancel off. This is the effect on the action of a tiny step in the B to D direction. That quantity, the effect on the action of a small step to the right, is the same at the beginning (A to C) as at the end (B to D). There is a quantity, therefore, that does not change as time goes on, provided the minimum principle works, and the symmetry principle of displacement in space is right. This quantity which does not change (the effect on the action of a small step to one side) is in fact exactly the momentum that we discussed in the last lecture. This shows the relation of symmetry laws to conservation laws, assuming the laws obey a principle of least action. They satisfy a principle of least action, it turns out, because they come from quantum mechanics. That is why I said that in the last analysis the connection of symmetry laws to conservation laws comes from quantum mechanics.Richard P. Feynman, The Character of Physical Law, (Random House, Inc. New York 1994, ISBN 0-679-60127-9), Chapter 4, pages 97 to 100

The Lagrangian proof is also intuitive: suppose you have a trajectory x(t) which is the minimum of S. Then you can perform an infinitesimal symmetry transformation on the trajectory, and you get S(x+dx), which is S(x) plus an integral over time of dS/dx times dx, where d is the variational change in S, the variational derivative. The bulk path is an infinitesimal variation of the bulk path, so there is no change in action, by the principle that the variations of S are zero on the true trajectory. So the variational change can only depend on the endpoints, because the path is a minimum, so you get that there is a quantity A(x_i)dx - A(x_f) dx which is zero summed over the two endpoints, which means there is a constant quantity along the trajectory. Feynman explains the theorem this way in "The Character of Physical Law".http://qr.ae/TU1ODh

• Problems you can solve just by looking at them: The meaning of Noether’s Theorem by Brian Skinner
• http://physics.stackexchange.com/questions/325916/laymans-version-of-noethers-theorem-or-the-intuition-behind-it/325920#325920

Concrete

The Noether theorem tells us that when there is some transformation $q \rightarrow q+\epsilon \delta q$ that leaves the action unchanged, there exists a conserved current ${d j \over dt} = 0$.

This Noether current is defined as

\begin{eqnarray} j \equiv {\partial L \over \partial \dot{q}} \delta q \end{eqnarray}

So formulated differently, Noether’s Theorem tells us that whenever there is a continuous symmetry of the action, there is a conserved quantity.

A concrete Example

Let's consider a projectile, which is described by the Lagrangian \begin{eqnarray} L = {1\over 2} m (\dot{x}^2 + \dot{y}^2) - mgy \label{eq:projectile} \end{eqnarray} This Lagrangian is unchanged under the transformation $x \rightarrow x+\epsilon$, where $\epsilon$ is sufficiently small constant. (Here, we have $\delta q=1$ in the notation from above). We can see this because $$x \rightarrow x+\epsilon \Rightarrow \dot{x} \rightarrow \dot{x}.$$

Therefore, Noether's theorem tells us that $$j = {\partial L \over \partial \dot{q}} \delta q = m \dot{x}$$ is conserved. We can now recognize that $m\dot{x}$ is the usual momentum.

Noether's theorem, therefore, tells us here that the invariance of the Lagrangian under translations $x \rightarrow x+\epsilon$ implies the conservation of momentum.

Derivation

We start with a Lagrangian $L=L(q,\dot{q})$ and consider an infinitesimal (= tiny tiny tiny) transformation \begin{eqnarray} q \rightarrow q+\epsilon \delta q \, . \end{eqnarray} Here $\epsilon$ denotes, as usual, an infinitesimal constant.

Acting with this transformation on our Lagrangian yields will give \begin{eqnarray} L(q,\dot{q}) \rightarrow L(q+\epsilon \delta q, \dot{q}+\epsilon \delta \dot{q}) = L(q,\dot{q})+\epsilon \delta q{\partial L \over \partial q}+\epsilon \delta \dot{q} {\partial L \over \partial \dot{q}} \end{eqnarray}

Now, if the Euler-Lagrange equations of motion are fulfilled by the path in question, then ${\partial L \over \partial q} = {d \over dt} {\partial L \over \partial \dot{q}}$, then under $q \rightarrow q + \epsilon \delta q$, \begin{eqnarray} L \rightarrow L + \epsilon \delta q {\partial L \over \partial q} + \epsilon \delta \dot{q} {\partial L \over \partial \dot{q}} = L + \epsilon \delta q {d \over dt} {\partial L \over \partial \dot{q}} + \epsilon {\partial L \over \partial \dot{q}}{d \over dt} \delta q = L + {d \over dt} \bigg({\partial L \over \partial \dot{q}} \epsilon \delta q\bigg) \end{eqnarray}

Therefore, under $q \rightarrow q+ \epsilon \delta q$, we have $\delta L = {d \over dt} \big({\partial L \over \partial \dot{q}} \epsilon \delta q \big)$.

We can now define the Noether Current $j$ \begin{eqnarray} j \equiv {\partial L \over \partial \dot{q}} \delta q \end{eqnarray}

Therefore, whenever we find some transformation $\delta q$ that leaves the action invariant ($\delta S = 0$), then ${d j \over dt} = 0$ holds.

In words, this means that the current $j$ is constant in time and therefore conserved.

Derivation of the conservation of energy

In the example above, we derived that momentum is conserved when the Lagrangian is invariant under spatial translations. Analogously, we can derive that energy is conserved when the Lagrangian is invariant under temporal translations.

To see this we consider the quantity \begin{eqnarray} {d L \over dt} = {d \over dt} L (q,\dot{q}) = {\partial L \over \partial q} {dq \over dt} + {\partial L \over \partial \dot{q}} {d\dot{q} \over dt} + {\partial L \over \partial t} \end{eqnarray} Now, because in most cases the Largangian $L$ does not depend explicitly on time, ${\partial L \over \partial t} = 0$, we have \begin{eqnarray} {d L \over dt} = {\partial L \over \partial q}\dot{q} + {\partial L \over \partial \dot{q}} \ddot{q} = \bigg({d\over dt} {\partial L \over \partial \dot{q}} \bigg) \dot{q} + {\partial L \over \partial \dot{q}} \ddot{q} = {d \over dt} \bigg({\partial L \over \partial \dot{q}} \dot{q}\bigg) . \end{eqnarray} Here we used the Euler-Lagrange equation to get to the second line.

We therefore have ${d L \over dt} = {d \over dt} \big({\partial L \over \partial \dot{q}} \dot{q}\big)$, or \begin{eqnarray} {d \over dt} \bigg({\partial L \over \partial \dot{q}}\dot{q} - L \bigg) = 0 . \end{eqnarray}

In general the Lagrangian for a non-relativistic system reads $L=T-V$ and therefore we have ${\partial L \over \partial \dot{q}} = {\partial T \over \partial \dot{q}}$ because the potential $V$ is usually a function of $q$ only. In most cases we have \begin{eqnarray} T \propto \dot{q}^2 \quad \Rightarrow\quad {\partial L \over \partial \dot{q}} \dot{q} = 2T . \end{eqnarray} Thus, we can conclude

$${\partial L \over \partial \dot{q}} \dot{q} - L = 2T - (T-V) = T+V = E,$$

which is the total energy of the system.

Here in this context the total energy $T+V \equiv H$ is also often called the Hamiltonian.

We can understand the connection between the Lagrangian and the Hamiltonian better by defining that ${\partial L \over \partial \dot{q}} \equiv p$ is the momentum of the system. The relationship between the Lagrangian and the Hamiltonian then reads \begin{eqnarray} p \dot{q} - L = H . \end{eqnarray}

In mathematical terms, the relationship between the Lagrangian and the Hamiltonian is given by a Legendre Transformation.

• A nice introduction is Noether's Theorem in a Nutshell by John Baez.
• Good descriptions can be found at http://users.physik.fu-berlin.de/~kleinert/b6/psfiles/Chapter-7-conslaw.pdf and here:
• http://www3.nd.edu/~kbrading/Research/WhichSymmetryStudiesJuly01.pdf
• http://snu.edu/Websites/snuokc/images/Physics/Noethers-Theorem.pdf
• A great book on Noether's theorems is "Emmy Noether's Wonderful Theorem" von Dwight E. Neuenschwander.

Noether's Theorem in the Hamiltonian formalism

Noether's theorem is especially transparent in the Hamiltonian formalism.

A symmetry is a transformation that leaves the Hamiltonian unchanged

$$ \delta H =0. $$

In general, the variation of $H$ is

$$ \delta H = \frac{\partial H}{\partial q_i} \delta q_i + \frac{\partial H}{\partial p_i} \delta p_i . $$

We can rewrite this using the generalized Hamiltons equations as

\begin{align} \delta H &= \frac{\partial H}{\partial q_i} \delta q_i + \frac{\partial H}{\partial p_i} \delta p_i \notag \\ & \alpha \frac{\partial H}{\partial q_i} \frac{\partial G}{\partial p_i} - \alpha \frac{\partial H}{\partial p_i} \frac{\partial G}{\partial q_i} + \mathcal{O}(\alpha^2)\notag \\ & \equiv \alpha \{ H,G\}, \end{align} where $ \{ H,G\}$ denotes the Poisson bracket and $G$ is a generating function.

Now, we can see that $G$ generates a symmetry if $ \{ H,G\} =0$.

In addition, we know that the equation of motion for $G$ is

$$\dot G = \{ G,H\} $$ which simply means that the Hamiltonian generates time translations.

Since the Poisson bracket is antisymmetric we can conclude that if $G$ is a symmetry: $ \{ H,G\} =0$ we automatically also have $ \{ G,H\} =0$ and thus $$\dot G = 0. $$

Therefore, if $G$ is a symmetry then $G$ is conserved. Equally, if $G$ is conserved we automatically know that it generates a canonical transformation.

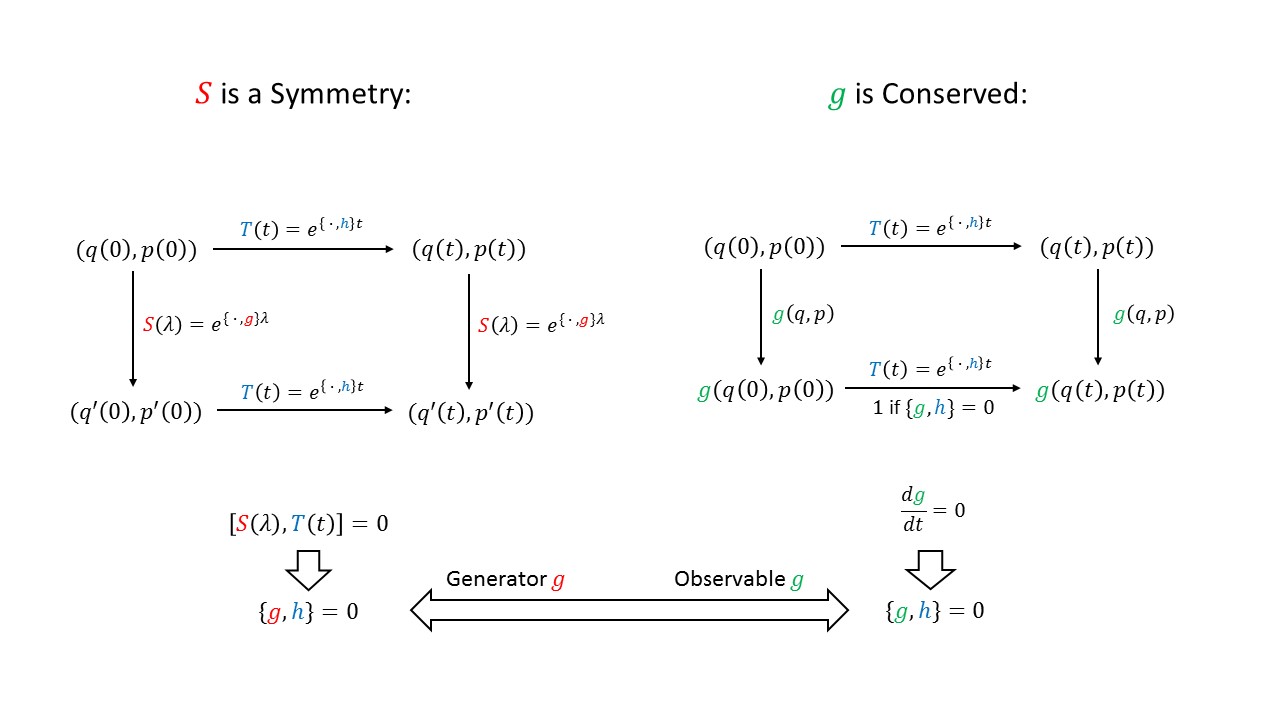
Graphical Summary

The diagram below shows the relationship between symmetry and conservation in the Lagrangian formalism for the case of a linear point transformation, such as a rotation. For a more detailed explanation see Fun with Symmetry.

The diagram below shows the relationship between symmetry and conservation in the Hamiltonian formalism. For a more detailed explanation see Fun with Symmetry.

Abstract

There are actually two theorems by Noether about the consequences of an action integral under a continuous group of transformations. For a nice description, see section 2.2 and 2.3 in https://arxiv.org/pdf/1510.07038.pdf and also the nice discussion in "Symmetries in Fundamental Physics" by Sundermeyer.

Noether's First Theorem

Her first theorem shows that if the action integral is invariant under a r-parameter Lie group $G_r$, then, provided the equations of motion are satisfied, we get $r$ conserved currents (called Noether currents).

For example, using this theorem we can derive that the invariance of the action under spatial and temporal translations and rotations implies conservation of linear momentum, energy and angular momentum.

Noether's Second Theorem

Her second theorem shows that if the action is invariant under an infinite dimensional group $G_{\infty r}$ (this means we use $r$-functions instead of $r$ parameters, which we actually do for gauge groups), then we get $r$ identities between the equations of motions, i.e. the Euler-Lagrange equations that we derive from the action.

These identities are called generalized Bianchi Identities.

Maybe the most famous example, are the homogeneous Maxwell equations, which are the generalized Bianchi identities that follow from the invariance under the electromagnetic gauge group.

If the action is invariant under both $G_{\infty r}$ and $G_r$ (as a rigid subgroup), then the conservation laws that we get from Noether's first theorem are direct consequences of the generalized Bianchi identities that we derive using Noether's second theorem.

Emmy Noether’s famous paper, Invariante Variationsprobleme, was published in Nachr. d. Konig. Gesellsch. d. Wiss. zu Gottingen, Math-phys. Klasse in 1918 [1], [2]. In this paper, Noether proves two different theorems. The First Theorem deals with “global” symmetries (generated by finite Lie groups) and states that these symmetries lead to conserved charges. The Second Theorem applies to local gauge symmetries (infinite dimensional Lie groups), containing arbitrary functions of spacetime (like Einstein’s theory of gravity) and shows that these gauge symmetries inevitably lead to relations among the equations of motion (e.o.m. onwards).

https://arxiv.org/pdf/1601.03616.pdf

Noether’s 1918 theorem [41] relating infinitesimal “global” symmetries to conservation laws, is a cherished cornerstone of modern theoretical physics; however, the second theorem (appearing in the same work) applicable to “local” symmetry remains somewhat obscure [43]. Our goal is to use Noether’s second theorem as a starting point for a general approach to Ward identities for gauge symmetry. In particular, we are motivated by recent new Ward identities for large gauge symmetry in gravity and QED [4–6, 8–13], and recent discussions in [37]. (This assertion is based, in part, on informal discussions. An important exception is 44, which introduced the authors to Noether’s second theorem)

https://arxiv.org/pdf/1510.07038.pdf

Noether's theorem in the Hamiltonian formalism

The analogue to Noether's theorem in the Lagrangian formalism is the moment map in the Hamiltonian formalism.

These moment maps provide a way of encoding of how the Lie group $G$ acts on the phase space. In addition, the moment maps give us a way to find the observables corresponding to the conserved quantities/generators of the symmetry $G$.

• see also Use the Moment Map, not Noether’s Theorem by P. Woit

The crucial object in the Hamiltonian formalism is the Poisson bracket of two observables, which can be thought of as the rate of change of the first along the flow given by the second.

So when we use the Hamiltonian $H$ as the generator, we end up with time evolution. Therefore for an observable $A$ without explicit time dependence we have

$$\frac{\mathrm{d}A}{\mathrm{d}t} = \{A, H\}.$$

Therefore, $A$ is a constant of motion (= does not change as time passes on) only if $\{A, H\} =0$.

However, we can equally consider the reverse Poisson bracket $\{H, A\}$. Here $A$ appears in the second slot and therefore this Poisson bracket represents the rate of change of $H$ along the flow generated by $A$. So if $A$ generates a symmetry of a system we expect that $\{H, A\}$ is true. This comes about because if the Hamiltonian remains unchanged by the flow generated by $A$ then also the equations of motion: $\dot q = \frac{\partial H}{\partial p}, \quad \dot p = - \frac{\partial H}{\partial q}$ remain unchanged under the same flow.

• If $\{H, A\} =0$ which means we have a symmetry of the Hamiltonian generated by $A$, then since the Poisson bracket is antisymmetric we automatically have
• $\{A, H\} =0$, which states that $A$ is a conserved quantity.

For example, if the Hamiltonian is invariant under translations, we have $\{H, p\}=0$ since $p$ generates translations. In turn, we automatically also have $\{p, H\}=0$ which means that momentum is conserved.

In general, the infinitesimal evolution under the transformation generated by any element $g$ of the Lie algebra of observables on our phase space, (parametrized by an abstract "angle" $\varphi$) is given by

$$ \partial_\phi F = \{G,F\}.$$

This has immediately important consequences because it means that if the Poisson bracket of $F$ and $G$ vanishes, they describe an infinitesimal transformation that is a symmetry for the other. So if the Poisson bracket of an observable with the Hamiltonian vanishes it means that this observable is invariant under time translations, i.e. a constant in time. Similarly, if the Poisson bracket of an observable and the generator of rotations (= angular momentum $L^i = \epsilon^{ijk}x^jp^k$) vanishes it is invariant under rotations.

More precisely, consider a "generator" $\delta G$ and some quantity $A$. The infinitesimal transformation, generated by $\delta G$ is:

$$A \to A+\delta A,\quad\quad \delta A = -\{\delta G, A\}. $$

Momentum

$\delta G = \epsilon_i p_i \quad \delta A = -\epsilon_i\{p_i, A\} = \epsilon_i\frac{\partial A}{\partial q_i},$ $\quad \Rightarrow \quad A(p_i,q_i)\to A(p_i,q_i)+\epsilon_i\frac{\partial A}{\partial q_i} = A(p_i,q_i+\epsilon_i)$ Therefore momentum is the generator of translations.

Angular Momentum

$$\delta G = \epsilon_i e_{ijk} p_jq_k \quad \delta A = -\epsilon_i e_{ijk} \{p_jq_k, A\}$$

Here $e_{ijk}$ is the Levi-Civita symbol. Expanding yeilds $\delta A = -\epsilon_i e_{ijk} \sum_\alpha \left(\frac{\partial p_jq_k}{\partial q_\alpha}\frac{\partial A}{\partial p_\alpha}-\frac{\partial p_jq_k}{\partial p_\alpha}\frac{\partial A}{\partial q_\alpha}\right) = -\epsilon_i e_{ijk}\left(p_j\frac{\partial A}{\partial p_k}+q_j\frac{\partial A}{\partial q_k}\right)$

$\quad \Rightarrow \quad A(p_i,q_i)\to A(p_i,q_i)-\epsilon_i e_{ijk}\left(p_j\frac{\partial A}{\partial p_k} + q_j\frac{\partial A}{\partial q_k}\right) = A(R_{ij}p_j,R_{ij}q_j)$ For infinitesimal rotations $R_{ij}$

So we conclude that angular momentum is the generator of rotations.

Energy

$\delta G = \epsilon H \quad \delta A = -\epsilon\{H, A\} = \epsilon\frac{d A}{d t},$

$\quad \Rightarrow \quad A(p_i(t),q_i(t))\to A(p_i(t),q_i(t))+\epsilon\frac{d A}{d t} = A(p_i(t+\epsilon),q_i(t+\epsilon))$

Therefore energy is the generator of time evolution.

Reading Recommendations:

• http://mathoverflow.net/questions/69055/reference-for-noethers-theorem
• Section 3.4.3 in http://math.ucr.edu/home/baez/classical/texfiles/2005/book/classical.pdf where he shows that the conserved quantities that arise from invariance under reparametrizations vanish and argues this is an example of a gauge symmetry.
• http://www.damtp.cam.ac.uk/user/tong/qft/qft.pdf
• https://physics.stackexchange.com/questions/19847/whats-the-interpretation-of-feynmans-picture-proof-of-noethers-theorem

Why is it interesting?

In 1915, Emmy Noether demonstrated that differentiable symmetries give rise to conservation laws. Her work is a foundational document in quantum theory because it verifies the ancient insight that what is most important in any physical system is what remains the same in the system as the system is changing.http://inference-review.com/article/woits-way

Noether's most famous first theorem connects each symmetry of a system with a conserved quantity.

Noether’s second theorem, is an old but somewhat underappreciated tool, which acquires new significance in light of recent developments. By combining the robustness of the path integral formalism with the elegance of Noether’s second theorem we find that writing down Ward identities for residual gauge symmetries becomes essentially automatic.https://arxiv.org/abs/1510.07038

FAQ

Is the converse of Noether's first theorem true: Every conservation law has a symmetry?

See https://physics.stackexchange.com/questions/24596/is-the-converse-of-noethers-first-theorem-true-every-conservation-law-has-a-sy

What conserved quantity corresponds to invariance under boosts?

See http://math.ucr.edu/home/baez/boosts.html

A further discussion can be found in the book "Physics from Symmetry" by Schwichtenberg

What about Noether's theorem in the Hamiltonian framework?

There’s a short (slightly mystifying) calculation always given to derive this. I’d like to argue that this is really not the best way to think about the implications of having a Lie group act on a physical system, that for this it’s better to take the Hamiltonian point of view. There the way symmetry principles work is:

For a function on phase space (or on a general symplectic manifold) you get a vector field. This is just Hamilton’s equations, giving the vector field for time evolution corresponding to any Hamiltonian function. The infinitesimal action of G on phase space gives a vector field for each element of the Lie algebra of G. The moment map takes an element of the Lie algebra to a function on phase space (the one corresponding to the vector field). I’m ignoring some subtleties here having to do with the relation between vector fields and functions not being quite one-to-one.

All of the basic examples of conservation laws in physics come about this way. The action of time translation gives the Hamiltonian function, space translation the momentum, rotations give the angular momentum, and phase transformations give charge. You can get these either as moment maps, or using Noether’s theorem.

The moment map however gives you much more, with phase space providing structure that is not visible just from the action. A simple example is the harmonic oscillator in 3 variables.

http://www.math.columbia.edu/~woit/wordpress/?p=7146

See also https://www.math.columbia.edu/~woit/wordpress/?p=7146 and also chapte 15 here https://www.math.columbia.edu/~woit/QM/qmbook.pdf and also Chapter 7 "Conserved Quantities are Momentum Maps" in the book "Symmetry in Mechanics" by Singer

What about conserved charges in gauge theories?

In section 3.5.1 http://math.ucr.edu/home/baez/classical/texfiles/2005/book/classical.pdf John Baez argues that gauge symmetries "are symmetries that permute different mathematical descriptions of the same physical situation—in this case reparameterizations of a path." And further that "These symmetries give conserved quantities that work out to equal zero!" ( He shows this explicitly in section 3.4.3)

Of course, there are gauge transformations (choices of ξ a ) where the boundary term is zero. Regge and Teitelboim noted that not all gauge transformations are on equal footing, and made the following classification:

• Proper gauge transformations are those choices of ξ a such that B[ξ] = 0. These form the class of ‘purely gauge’ transformations that do not change the physics state of a system. Their generator is purely a constraint. Note that the value of B[ξ] does not only depend on the choice of ξ a but also on the boundary values of the field Aϕ. We discuss this is detail below.
• Improper gauge transformation are those choices of ξ a such that B[ξ] 6= 0. This class of gauge transformations must not be considered “pure gauge”. They do change the state of the system. Let us put this on firm basis. Suppose we have a parameter ξ a and we act on Aa i generating the transformation δAa a = Diξ a , then if the generator G[ξ] is not zero (B[ξ] is not zero) then this transformation is physical, it can be measured in an experiment.

As we have mentioned, gauge symmetries do not carry Noether charges. In the presence of boundaries, however, the sub-group of gauge symmetries defining “improper gauge transformations” is not generated by constraints, they do change the physical state, and have non-zero Noether charges. Nonetheless, improper gauge transformations are still symmetries of the action. The difference with a proper gauge symmetry is that the former are generated by non-zero quantities. But the transformations itself -irrespective of its generator– is the same as always, and is a symmetry. As usual in Hamiltonian mechanics, the generator of a symmetry is conserved. The goal of this paragraph is to prove this statement explicitly.

https://arxiv.org/pdf/1601.03616.pdf

Noether’s theorem told us that these symmetries give rise to conservation laws. Do we now have an infinite number of conservation laws? The answer is no! Gauge symmetries have a very different interpretation than the global symmetries that we make use of in Noether’s theorem. While the latter take a physical state to another physical state with the same properties, the gauge symmetry is to be viewed as a redundancy in our description. That is, two states related by a gauge symmetry are to be identified: they are the same physical state.

page 126 in http://www.damtp.cam.ac.uk/user/tong/qft/qft.pdf

Is there a symmetry associated to the conservation of information?

see https://physics.stackexchange.com/questions/41765/is-there-a-symmetry-associated-to-the-conservation-of-information

History

• Colloquium: A Century of Noether's Theorem by Chris Quigg
• See also Chapter 1 in The Noether Theorems: Invariance and Conservation Laws in the Twentieth Century

by Yvette Kosmann-Schwarzbach