Intuitive

Particle Content

• Let's have a coffee with the Standard Model of particle physics! by Julia Woithe, Gerfried J Wiener and Frederik F Van der Veken
• The Theory of Almost Everything by Robert Oerter
• A nice video explanation can be found here: https://cds.cern.ch/record/1279356
• http://axelmaas.blogspot.de/2010/09/symmetries-of-standard-model.html

Concrete

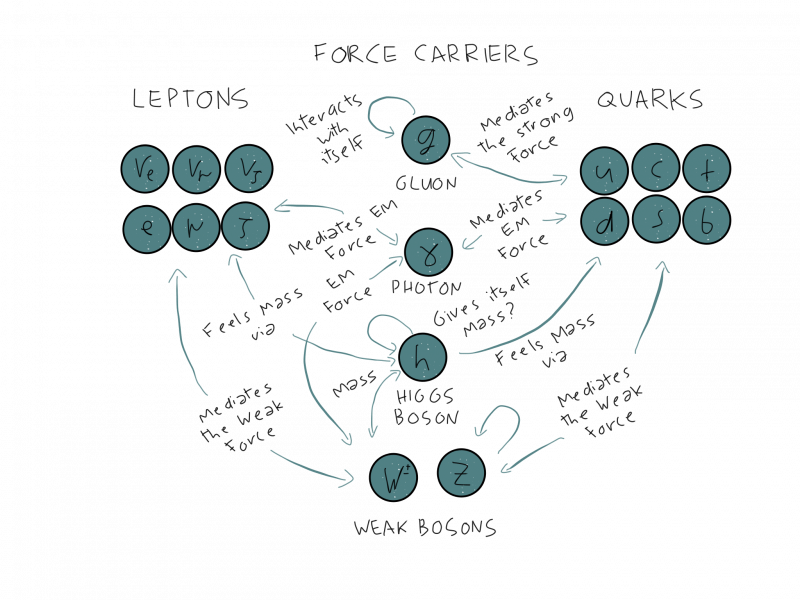
At the heart of the Standard Model is the gauge symmetry $$ G\ =\ SU(3)_C\times SU(2)_L\times U(1)_Y\, . $$ The $SU(3)_C$ mixes the three colors of the quarks and antiquarks, the $SU(2)_L$ the weak isospin, and the $U(1)_Y$ couples to the weak hypercharge $Y$.

The electroweak symmetry $SU(2)_W\times U(1)_Y$ is spontaneously broken by the scalar field $\langle H \rangle \neq0$ down to $U(1)_{EM}$.

As a result, the $W^\pm$ and $Z^0$ vector particles become massive ($M_W\approx80.4$ GeV, $M_Z\approx91.2$ GeV) while the photon $\gamma$ remains massless.

Standard Model Lagrangian

Source: http://blogs.discovermagazine.com/cosmicvariance/2006/11/23/thanksgiving/

• A nice overview of the various terms in the Standard Model Lagrangian can be found here. A short non-technical discussion of the various terms can be found here.

Particle Content

The field content of the standard model is nicely summarized here

The Gauge Bosons

The photon couples to the electric charge which is a linear combination of hypercharge and weak isospin $$ q\ =\ T^3\ +\ Y . $$

The photon is responsible for electromagnetic interactions. Since it is massless the electromagnetic forces are long-ranged.

The $W^\pm$ and $Z^0$ bosons are responsible for the weak interactions. Since both are massive the weak force is short-ranged.

The bosons responsible for the strong force are called gluons. This name stems from the fact that they ``glue'' the quarks and antiquarks together. Bound states made of quarks and antiquarks are called baryons and mesons. The strong forces become stronger with rising distance between two color-chared particles. As a result individual quarks, antiquarks, or gluons can't be isolated. This is known as confinement. Only $SU(3)_C$ singlets can be observed.

---

The Fermions

All quarks come in 3 colors $c=1,2,3$ and 6 additionally six flavors $f=u,d,s,c,b,t$ called `up', `down', `strange', `charm', `bottom', and `top'.

The left-handed quarks form 9 $SU(2)_L$ doublets: $$(u,d)_L, (c,s)_L, (t,b)_L$$ (3 for each color)

The right-handed quarks are $SU(2)_L$ singlets.

This curious difference between left-handed and right-handed quarks means that weak interactions disrespect the parity symmetry. The bosons $W^\pm$ only couple to the left currents $J^\mu_L=V^\mu-A^\mu$ and don't care about the right currents $J^\mu_R=V^\mu+A^\mu$.

The same is true for the leptons $e^-$, $\mu^-$, $\tau^-$, and the 3 neutrino species.

The left-handed leptons live in three $SU(2)_L$ doublets: $$(\nu_e,e^e)_L, (\nu_\mu,\mu^-)_L, (\nu_\tau,\tau^-)_L$$.

The right-handed charged leptons $e^-_R$, $\mu^-_R$, $\tau^-_R$ are $SU(2)_L$ singlets. So far right-handed neutrinos were never observed.

Standard Model Interactions

Source: Image by Garyzx published under the CC BY-SA 3.0 licence

• A nice introduction to the standard model is the series by Flip Tanedo: http://www.quantumdiaries.org/2010/02/14/lets-draw-feynman-diagams/
• And also The Standard Model of Electroweak Interactions by A. Pich
• The best resource for the correct Feynman rules of the standard model is A resource for signs and Feynman diagrams of the Standard Model by Jorge C. Romao. The thing is that there are many different conventions and these authors develop a notation that allows us to map them all onto each other. For a short summary from the same author see Advanced Quantum Field Theory by Jorge Crispim Romao

Abstract

• See The Structure and Interpretation of the Standard Model, Volume 1 and Volume 2 by Gordon McCabe
• Symmetries of the Standard Model by Scott Willenbrock 

Why is it interesting?

The Standard Model of particle physics is a superb monument attesting to the inner beauty of nature and the power of human logical deduction. It is astounding how natural phenomena, in all their complexity, can be summarised by a single principle – the gauge principle – and described by a compact set of equations. And it is equally astounding how humans have been able to crack this secret. Along this path, the synthesis of general relativity with the physical laws derived in the microworld has led to the ΛCDM model, which can successfully describe a huge array of cosmological observations, the present largescale structure of the universe and its early history, in terms of a handful of parameters.The Dawn of the Post-Naturalness Era by Gian Francesco Giudice

See also:

• Open Problems, for a summary of unsolved problems and puzzles in the standard model.
• Speculative Theories, for a list of proposed extensions and modifications of the standard model.

Experimental Tests

• The canonical reference for all data related to the standard model is the review of the particle data group, which is published each year.

FAQ

What is the symmetry group of the standard model?

The spacetime symmetry group of the standard model is the Poincare group. The Lie algebra of the standard model is

$$ \mathfrak{su}(3)_C \times \mathfrak{su}(2)_L \times \mathfrak{u}(1)_Y .$$

However, the corresponding Lie group is not necessarily

$$ SU(3)_C \times SU(2)_L \times U(1)_Y \, , $$

but could be

$$ SU(3) \times U(2) $$

or

$$ U(3) \times SU(2) $$

or

$$ S(U(3) \times U(2)) \, , $$

which all have the same Lie algebra. (Source)

There are thirteen connected Lie groups' with the same Lie algebra as $SU(3)\times SU(2) \times U(1)$. […] We can eliminate choices 1—4 by demanding that the gauge group be compact. Choices 9—13 may be removed from consideration by using the fact that the true non Abelian group of the quarks and leptons in the standard model is $SU(3) \times SU(2)$, since color triplet and weak doublet representations exist in nature.Note that the simply connected universal covering group of all 13 groups above is $SU(3) \times SU(2) \times R$, while $SU(3) \times SU(2) \times U(1)$ is the covering group for groups 5—13. As discussed previously by O'Raifeartaigh, there then remain four possible true symmetry groups for the standard model: $$SU(3) \times SU(2) \times U(1)$$ $$ SU(3) \times U(2) $$ $$ U(3) \times SU(2) $$ $$ S(U(3) \times U(2)) \, . $$ [..] It should be understood from the beginning that the groups $U(3) \times SU(2)$, $SU(3) \times U(2)$, and $S(U(3) \times U(2) )$ yield the same perturbative quantum field theory as $SU(3) \times SU(2) \times U(1)$, since perturbative effects depend only on the Lie algebra. Whether or not the four groups lead to different nonperturbative effects is to the author's knowledge still an open question. Global structure of the standard model, anomalies, and charge quantization by Joseph Hucks

What people usually call the gauge group of the Standard Model: SU(3) × SU(2) × U(1) actually has a bit of flab in it: there's a normal subgroup that acts trivially on all known particles. This subgroup is isomorphic to Z/6. If we mod out by this, we get the "true" gauge group of the Standard Model: G = (SU(3) × SU(2) × U(1))/(Z/6) And, this turns out to have a neat description. It's isomorphic to the subgroup of SU(5) consisting of matrices like this: (g 0) (0 h) where g is a 3×3 block and h is a 2×2 block. For obvious reasons, I call this group S(U(3) × U(2)) If you want some intuition for this, think of the 3×3 block as related to the strong force, and the 2×2 block as related to the electroweak force. A 3×3 matrix can mix up the 3 "colors" that quarks come in - red, green, and blue - and that's what the strong force is all about. Similarly, a 2×2 matrix can mix up the 2 "isospins" that quarks and leptons come in - up and down - and that's part of what the electroweak force is about. […] l assume that one way or another, you're happy with the idea of S(U(3) × U(2)) as the true gauge group of the Standard Model! Maybe you understand it, maybe you're just willing to nod your head and accept it.

http://math.ucr.edu/home/baez/week253.html

r. Correlation functions of local operators in R1,3 depend only on the Lie algebra of the gauge group and are unaffected by global issues such as the choice of Γ. This means that no current experiment can distinguish between the four possibilities. Nonetheless, the physics in flat space can depend in subtle ways on Γ (and in more dramatic ways when spacetime has interesting topology). The purpose of this paper is to describe the crudest differences between the theories: the spectrum of line operators and the periodicities of theta angles.https://arxiv.org/pdf/1705.01853.pdf

A great discussion of these things with awesome illustrations can be found in section 1.4 and at page 26 in Some Elementary Gauge Theory Concepts by Hong-Mo Chan, Sheung Tsun Tsou:

As a further example, consider the standard electroweak theory. In this case, the gauge group was identified in Section 1.4 as $U(2)$ or $[SU(2)\times U(1)]/Z_2$, by which we meant that $U(2)$ can be obtained from $SU(2) \times U(1)$ by identifying certain pairs of elements as explained in the paragraph after 1.4.9. The group $SU(2) \times U(1)$ itself consists of couples of elements from respectively the groups $SU(2)$ and $U(1)$, which we mai represent symbolically as points inside the rectangle in Figure 2.8 where the vertical axis represents the group $SU(2)$ and the horizontal axis $U(1)$, and the parallel edges of the rectangle are understood to be identified so as to make the rectangle into a "hyper torus".

page 26 in Some Elementary Gauge Theory Concepts by Hong-Mo Chan, Sheung Tsun Tsou

What is the true gauge group of the standard model?

The Lie algebra of the standard model is

$$ \mathfrak{su}(3)_C \times \mathfrak{su}(2)_L \times \mathfrak{u}(1)_Y .$$

However, the corresponding Lie group is not necessarily

$$ SU(3)_C \times SU(2)_L \times U(1)_Y \, , $$

but could be

$$ SU(3) \times U(2) $$

or

$$ U(3) \times SU(2) $$

or

$$ S(U(3) \times U(2)) \, , $$

which all have the same Lie algebra. (Source)

There are thirteen connected Lie groups' with the same Lie algebra as $SU(3)\times SU(2) \times U(1)$. […] We can eliminate choices 1—4 by demanding that the gauge group be compact. Choices 9—13 may be removed from consideration by using the fact that the true non Abelian group of the quarks and leptons in the standard model is $SU(3) \times SU(2)$, since color triplet and weak doublet representations exist in nature.Note that the simply connected universal covering group of all 13 groups above is $SU(3) \times SU(2) \times R$, while $SU(3) \times SU(2) \times U(1)$ is the covering group for groups 5—13. As discussed previously by O'Raifeartaigh, there then remain four possible true symmetry groups for the standard model: $$SU(3) \times SU(2) \times U(1)$$ $$ SU(3) \times U(2) $$ $$ U(3) \times SU(2) $$ $$ S(U(3) \times U(2)) \, . $$ [..] It should be understood from the beginning that the groups $U(3) \times SU(2)$, $SU(3) \times U(2)$, and $S(U(3) \times U(2) )$ yield the same perturbative quantum field theory as $SU(3) \times SU(2) \times U(1)$, since perturbative effects depend only on the Lie algebra. Whether or not the four groups lead to different nonperturbative effects is to the author's knowledge still an open question. Global structure of the standard model, anomalies, and charge quantization by Joseph Hucks

The Lie algebra of the Standard Model is the Lie algebra of SU(3)xSU(2)xU(1). But, the Lie group corresponding to this Lie algebra is not unique. The true Lie group of the Standard Model can be determined by requiring that the corresponding group representations are faithful. A mathematical discussion of this point can be found in John C. Baez, The True Internal Symmetry Group of the Standard Model.

Given the particle content of the the Standard Model, the Lie group of the Standard Model is in fact SU(3)xSU(2)xU(1)/Z6. Details can be found in:

B.L.G. Bakker, A.I. Veselov and M.A. Aubkov, Phys. Lett. B 583 (2004) 379. HTML] M.A. Zubkov, Phys. Lett. B 649 (2007) 91. HTML]

http://scipp.ucsc.edu/~haber/ph218/

A nice discussion of this can also be found at page 272 in "Quantum Field Theory - A Modern Perspective" by V. P. Nair.

What questions are left open by the standard model?

See Open Problems

What symmetries do exist in the standard model and what is their experimental status?

see https://physics.stackexchange.com/questions/97896/symmetries-of-the-standard-model-exact-anomalous-spontaneously-broken

History

• The Rise of the Standard Model: A History of Particle Physics from 1964 to 1979 by Lillian Hoddeson
• Resource Letter: The Standard Model and Beyond by Jonathan L. Rosner
• https://inference-review.com/article/the-standard-model by Sheldon Glashow