Intuitive

geometry asks, “Given a geometric object X, what is its group of symmetries?” Representation theory reverses the question to “Given a group G, what objects X does it act on?” and attempts to answer this question by classifying such X up to isomorphism." Source

Concrete

A Lie group is in abstract terms a manifold, which obeys the group axioms. A representation is a special type of map $R$ from this manifold to the linear operators of some vector space. The map must obey the condition $$ R(gh) = R(g) R(h), $$ where $g$ and $h$ are elements of the group. This means the map must preserve the product structure of the group and the mathematically notion for such a map is homomorphism.

In practice a representation is a map that maps each element of the abstract group onto a matrix. (Matrices are linear operators over a vector space.)

(There are other representations, where the group elements aren't given as matrices, but in physics matrix representations are most of the time sufficient).

Take note that it is possible to introduce a more general notion, called a realisation of the group. A realisation maps the group elements onto the (not necessarily linear) operators over an arbitrary (no necessary vector-)space. However, in physics we usually only deal with representations, because our physical objects live in vector spaces.

Characterization of Representations

One way to label representations is by using the Casimir Operators.

Another possibility is given by the Weyl character formula. This formula allows to compute the "character" of a group. A "character" is a function that yields a number for each group element. Thus, one can compute which representation one is dealing with by computing this "character" function. If two representations that could be constructed very differently are actually the same their character functions are the same.

The diagram below is a graphical illustration of representation theory.

At the top left is the (abstract) Lie group. To the right are two matrix representations of this group; one is k dimensional and one is r dimensional. A group can have any number of representations, but only two are shown for illustration. Below the group is the (abstract) Lie algebra together with two of its matrix representations. The Lie-group and the Lie-algebra representations act on the vector spaces on the far right. These vector spaces are also called representation spaces to distinguish them from other vector spaces (such as the Lie algebra). The dimensionality of the representation equals the dimensionality of the representation space it acts on.

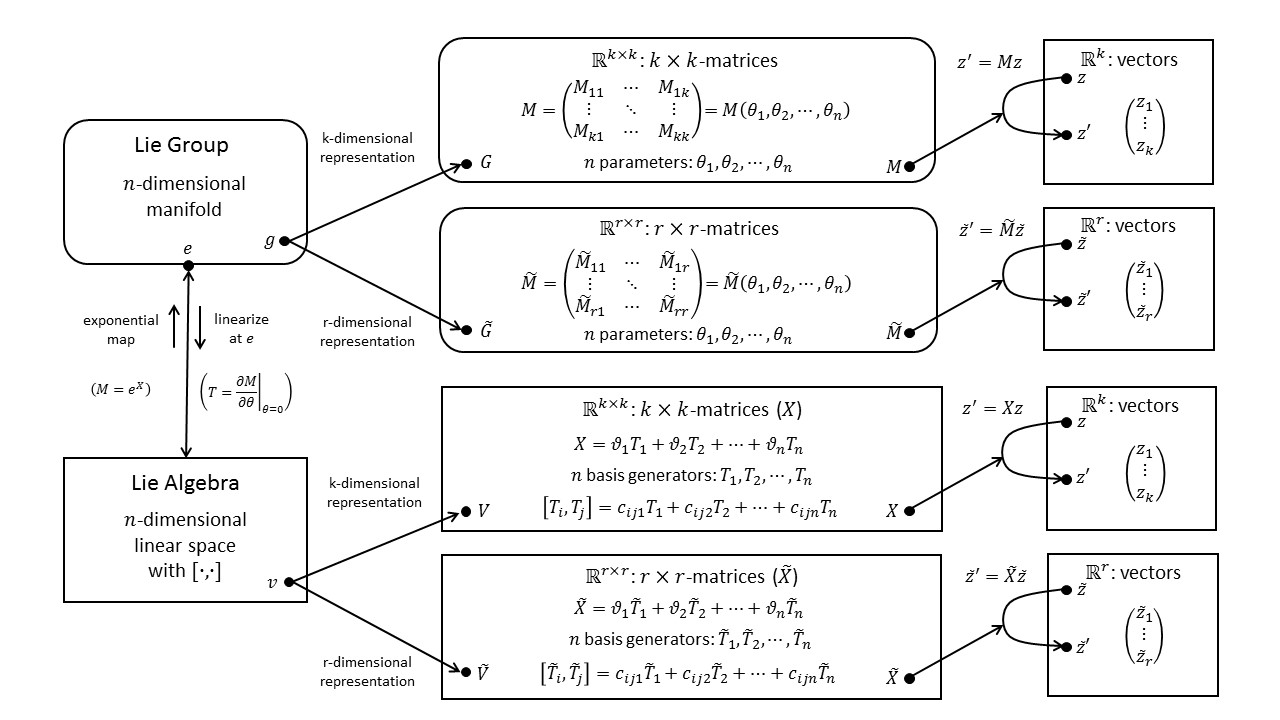
For a more detailed explanation of this diagram and much more, see Fun with Symmetry.

For more details, take a look at

• Short Introduction to and Motivation for Representation Theory
• What’s so special about the adjoint representation of a Lie group?
• http://www.damtp.cam.ac.uk/user/ch558/pdf/Representations.pdf

Abstract

Mathematically a representation is a homomorphism from the group to the group of automorphisms of something.

Why is it interesting?

In physics, we are usually interested in what a group actually does. A group is an abstract object, but representation theory allows us to derive how a group actually acts on a system.

In addition, representation theory is what allows us to understand elementary particles. For example, by using the tools of representation theory to analyze the Lorentz group (=the fundamental spacetime symmetry group), we learn what kind of elementary particles can exist in nature. Moreover, representation theory is crucial to understand what spin is, which is one of the most important quantum numbers.