Intuitive

A pendulum consists of a freely hanging massive bob at the end of a rod. When we move the bob a little to one side it starts swinging.

We usually describe it by measuring how far the bob has moved from its original position where it just hangs freely. How the pendulum swings depends crucially on the length of the rod and the strength of the gravitational field. A pendulum on the moon swings differently than a pendulum on earth.

An important observation is that the swinging of the pendulum does not depend on the mass of the bob.

A pendulum is right after a harmonic oscillator the simplest physical system we can study. In fact, if the pendulum only swings a little it is a harmonic oscillator. The difference between the harmonic oscillator and the pendulum only become important for large swings.

• see also the nice interactive demonstration here.

Concrete

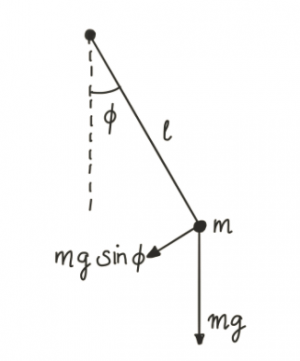
A normal pendulum hangs freely in a uniform gravitational field of strength $g$ on a rod with length $l$. The excitation above the ground state is measured by the angle $\phi$. At the end of the pendulum, we have a bob of mass $m$. This is shown in the picture on the right-hand side.

The only force that acts on the pendulum is the gravitational force $F= mg \sin\phi $. Therefore, using Newton's second law the correct equation of motion for the pendulum is

$$m\frac{d^2 x}{dt^2}= - mg \sin \phi .$$

Now we need to get rid of the arc length on the left-hand side using $x = l \phi$. This yields

$$m\frac{d^2 x}{dt^2}= - m\frac{g}{l} \sin \phi .$$

It is important to note that we can remove mass $m$ from the equation because it appears on both sides:

$$\frac{d^2 x}{dt^2}= - \frac{g}{l} \sin \phi .$$

The swinging of the pendulum, therefore, does not depend on the mass of the bob.

Small Angle Approximation

The equation of motion of the pendulum is a non-linear equation which is hard to solve. However we can simplify it for the case when only small swings are happening. Then we can use the small angle approximation $\sin({\theta)} \approx \theta$.

This yields the equation \[\frac{d^2\theta}{dt^2} = -\frac{g}{L}\theta\] which can be solved to give the familiar equation for the harmonic oscillator \[\theta = A\sin({\beta t + \phi}), \beta = \sqrt{\frac{g}{l}}\] where $A$ is the amplitude and $\phi$ is the constant phase offset.

The Pendulum in the Lagrangian Formalism

The kinetic energy of the pendulum is

$$T=\frac{1}{2}ml^2(\frac{d\theta}{dt})^2$$

and the potential energy in the gravitational field of the earth

$$ U=mgl(1-cos\theta).$$

The Lagrangian of the pendulum is therefore

$$ L = T-U= \frac{1}{2} ml^2\dot{\theta}^2 - mgl (1-cos \theta), $$ where $\dot{\theta}\equiv d\theta /dt $ denotes the time derivative.

Using the Euler-Lagrange equation we can derive the corresponding equation of motion

$$\frac{d^2\theta}{dt^2}+\frac{g}{l}sin\theta=0 .$$

• For a nice complete discussion, see The Pendulum: A Case Study in Physics by Gregory L. Baker and James A. Blackburn

Abstract

The phase space of a pendulum

• A thorough discussion can be found in Quantum pendulum by R. Aldrovandi and P. Leal Ferreira

Why is it interesting?

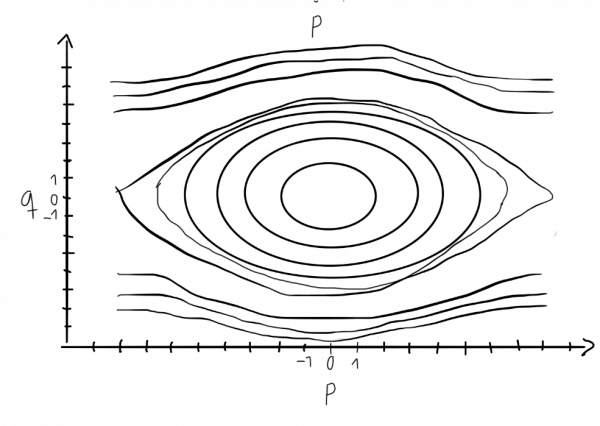
The pendulum is one of the most important basic physics systems.

Understanding the pendulum is crucial to understand topics as advanced as, for example, Solitons or the QCD vacuum.

In addition, it is ideal to understand the notion dimensional analysis.

History

• Time for Science Education - How Teaching the History and Philosophy of Pendulum Motion can Contribute to Science Literacy by Michael R. Matthews