Why is it interesting?

Feynman diagrams do not describe everything that can happen in a quantum field theory. There can be classical solutions of the field equations that describe larger lumps of field excitations that aren't describable by Feynman diagrams.

Classical solutions of the field equations with finite energy are called solitons.

Such solutions are important to describe, for example, the vacuum of a theory. A famous example is the QCD vacuum which can only understand with the help of instantons.

In addition, there is an old dream that all elementary particles could be explained as topological solitons. (There are lots of problems with this idea, but at least, instantons come somewhat close.)

While solitons are rare in particle physics, they are found frequently in condensed matter physics.

Important examples of solitons are:

• Magnetic Monopoles - usually in 3+1 dimensions
• Sphalerons - usually in 3+1 dimensions
• Instantons - usually in 4 dimensions
• Vortices - usually in 2+1 dimensions
• Kinks - usually in 1+1 dimensions

Soliton equations are special, but they are by no means unimportant; they arise in such diverse areas of applied science as hydrodynamics, nonlinear optics, plasma dynamics, meteorology, Josephson type superconductive devices, nonlinear acoustics, oceanography, domain wall dynamics, dislocation theory, nonlinear electric filters, and in the theory of elementary particles.

http://garfield.library.upenn.edu/classics1979/A1979HF81700001.pdf

Layman

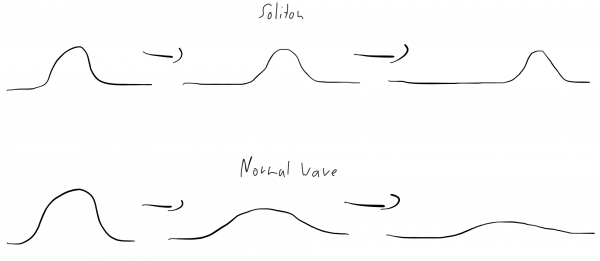
A soliton is a curious type of stable wave. Usually, waves vanish after some time. Think of a stone that gets thrown into some water. The stone will cause waves. At first, these waves will be large, but quickly get smaller and smaller until they are no longer visible. The waves flattens out. This process is known as dissipation.

In contrast, a soliton does not dissipate its energy but remains its form over a long time, possibly infinitely.

Before suggesting why the paper has been so often cited, it is appropriate to explain what the term soliton means. As coined by Zabusky and Kruskal, this term is generic for special solitary wave solutions of certain nonlinear wave equations.

What then is a solitary wave? It is a pulse-like wave that travels with constant speed and shape; the effects of dispersion on the wave shape are just balanced by those of nonlinearity. There is just enough yin for the yang; it is a dynamically self-sufficient object, a ‘thing.’

Solitons are solitary waves that preserve their speeds and shapes after mutual collision. They play a role in the construction of complete solutions for the nonlinear wave equation that corresponds to the role played by Fourier components in the construction of solutions for linear wave equations.

http://garfield.library.upenn.edu/classics1979/A1979HF81700001.pdf

“A solitary wave travels without changing its shape, size, or, speed” J. Scott Russell, “Report on waves”

Student

A soliton is a wave-packet that keeps a stable shape while propagating. The defining features of a soliton are:

1. A soliton is of permanent form, which basically means that they are static (=time independent) solutions of the field equations
2. A soliton is localized within a finite region. In other words, its energy and spatial size is finite.
3. When a soliton interacts with another soliton it emerges from the collision in exactly the same shape it had before. Only a phase shift is possible.

Solitons are stable through the interplay of dissipation and non-linearity of the underlying wave equations.

• Dissipation happens because a wave packet is a superposition of waves with different wave-lengths and usually waves with different wave-lengths travel with different velocities.
• Non-linearity of the wave equations can result in waves that get steeper over time. A good example are the waves that can be observed at a beach.

Recommended Textbooks

• Solitons and Instantons by Ramamurti Rajaraman - is the best introductory book on solitons and related topics
• Topological Solitons by Manton and Sutcliff - is the second-best introductory book on solitons
• Classical lumps and their quantum descendants by Sidney Coleman - a "must read" lecture for anyone interested in solitons
• Classical Solutions in Quantum Field Theory: Solitons and Instantons by Erick Weinberg - contains several helpful chapters
• Classical Theory of Gauge Fields by Rubakov - is great to dive deeper and contains many alternative perspectives that can't be found anywhere else.

• Quarks, Leptons & Gauge Fields by Kerson Huang - contains several extremely helpful chapters regarding solitons etc.
• Quantum Field Theory by Lewis H. Ryder - contains, like Huang's book - a particular nice chapter on solitons and instantons

Researcher

Many field theoretical models at the heart of our present understanding of elementary particles and their interactions have topological defects between the solutions of their classical counterparts. Because hadrons, particles interacting via strong subnuclear forces, are of two types -heavy (baryons), and light (mesons)- it was tempting to think of them respectively as quantum solitons and light quanta. This point of view was pioneered by Skyrme and Finkelstein as early as the sixties. The first author even proposed a variation that encompasses solitons on the (at that time fashionable) Gell-Mann/Levy sigma model of strong interactions . In the Skyrme model, the solitons, usually referred to as Skyrmions, would describe the classical limit of baryons whereas mesons were associated with light quanta.https://arxiv.org/pdf/hep-th/0611180.pdf

• Geometry of Yang-Mills Fields by M. F. ATIYAH plus chapters in
• Geometry of Physics by Frankel and
• Topology and Geometry for Physicists by Nash and Sen

Examples

Example1

Example2:

FAQ

–>Do we really only care about finite energy solutions?#

At first, it seems completely reasonable to consider finite energy field configurations. However, take note that usually in QFT we only deal with field configurations with infinite field energy. The "normal" wave solutions of our equations of motion etc. that we use to describe elementary particles are classical infinite energy solutions. Source: page 56 in Quarks, Leptons & Gauge Fields by K. Huang

See also Coleman, The Use of Instantons page 284 in Aspects of Symmetry: "In fact, it is configurations of finite energy that are unimportant; to be precise, they form a set of measure zero in function space. […] The only reason we are interested in configurations of finite action is that we are interested in doing semiclassical approximations, and a configuration of infinite action does indeed give zero if it is used as the center point of a Gaussian integral." )

←-

History

Solitons were first described in 1834 by John Scott Russell:

I was observing the motion of a boat which was rapidly drawn along a narrow channel by a pair of horses, when the boat suddenly stopped – not so the mass of water in the channel which it had put in motion; it accumulated round the prow of the vessel in a state of violent agitation, then suddenly leaving it behind, rolled forward with great velocity, assuming the form of a large solitary elevation, a rounded, smooth and well-defined heap of water, which continued its course along the channel apparently without change of form or diminution of speed. I followed it on horseback, and overtook it still rolling on at a rate of some eight or nine miles an hour, preserving its original figure some thirty feet long and a foot to a foot and a half in height. Its height gradually diminished, and after a chase of one or two miles I lost it in the windings of the channel. Such, in the month of August 1834, was my first chance interview with that singular and beautiful phenomenon which I have called the Wave of Translation.[2]