Intuitive

• A nice overview is given here: https://profmattstrassler.com/articles-and-posts/particle-physics-basics/the-known-apparently-elementary-particles/
• Why not start with quarks? Teachers investigate a learning unit on the subatomic structure of matter with 12-year-olds by Gerfried J. Wiener, Sascha M. Schmeling and Martin Hopf
• How big is an electron? by Brian Skinner

Concrete

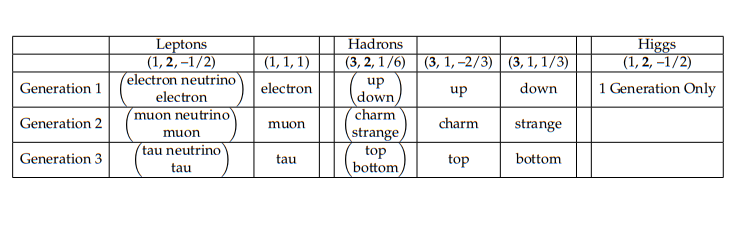
In the 1970’s, high energy physicists pursued Lie algebra theory as a valuable tool to characterize all the gauge interactions. These are now understood to be SU(3) for the strong force (which describes the interacations between quarks, which are the constituents of hadrons such as the proton), and SU(2) × U(1) for both the weak and electromagnetic interactions of quarks and leptons (such as the electron). This is an important feature of the standard model of particle physics [YM,We,Sa,Gl]. Grand unification was an effort to combine these symmetries as subgroups of a unifying group such as SU(5). Superstring unification provides an alternative mechanism to combine symmetries.

The interpretation of fundamental force laws in terms of group theory is now commonly understood in terms of E. Noether’s theorem which identifies the elements of the Lie algebra with the charges conserved in the interactions [No]. The symmetry is used to label the physical states: the eigenvalues of the Cartan subalgebra are the quantum numbers of the elementary particles. The quantum numbers are known as charge, spin, hypercharge, isospin, etc. depending on which group is being considered. Modern high energy theorists effectively think of the elementary particles of the strong, weak and electromagnetic forces as irreducible representations of the direct product of the Poincar´e group and SU(3) × 2 SU(2) × U(1). Selection rules derived from the conserved charges limit allowed transitions of quantum numbers. Explicit solutions of four-dimensional quantum field theory transition amplitudes, however, are known only in a perturbative expansion, i.e. they are not known exactly. This weak coupling perturbative approximation is extremely useful in electroweak theory, but the strong coupling problem of why the quarks are confined inside the hadrons remains more elusive

https://arxiv.org/pdf/hep-th/9601117.pdf

Recall that in the flat spacetime case the particle states are labeled by the Poincar´e label (p, λ), whose values are closely related to the UIR label (m, s); m is used to define the mass-shell condition and s determines the range of λ. We identified m with the mass of the field quanta, and s with the spin. In a group theoretical sense, we associate these parameters with the eigenvalues of the Casimir operators (see section 3.5).

http://thep.housing.rug.nl/sites/default/files/theses/Master%20thesis_Marco%20Boers.pdf

Abstract

A question not often addressed when discussing the standard model is how one describes physical particles. Taking the electron as an example, the assumption usually made is that the free Dirac spinor in the interacting theory, at asymptotic times, can be viewed as an electron since ‘the coupling switches off’. This would mean that what is being caught in a detector is really a free fermion. The problem here, of course, is that in QED and QCD the coupling does not switch off, and assuming it does so generates infrared divergences. As a result, the spinors do not become free even at asymptotic times [1, 2], nor do they ever become gauge invariant. […]

The physical picture is of a matter particle surrounded by a cloud of ‘photons’, neither of which are individually observable, but which together constitute a gauge invariant, physical particle. This description is nonlocal, which is an immediate consequence of gauge invariance, but observables calculated with our states are manifestly local and correctly reproduce classically expected physics.

Stability, creation and annihilation of charges in gauge theories by Anton Ilderton, Martin Lavelle, David McMullan

• http://math.ucr.edu/home/baez/qg-spring2003/elementary/
• See http://physics.stackexchange.com/questions/33350/particle-as-a-representation-of-the-lorentz-group
• A closer look at the elementary fermions by Maurice Goldhaber

First of all, for a Lorentz-invariant theory the space of single-particle states for a given particle species must be the basis for an irreducible representation of the Lorentz group. Indeed, if the representation were reducible, there would be different states that cannot be brought into one another by any Lorentz transformation. In this case it is natural to talk of different particle species rather than of different states of the same particle. […] Massless particles have no rest-frame—thus there is no reference frame where we can apply our non-relativistic QM knowledge about rotations and spin.

http://phys.columbia.edu/~nicolis/GR_from_LI.pdf

Particles can be elementary or composite. An elementary particle cannot be decomposed into parts. We do not have an exact criterion for elementary particles. However, Wigner has proposed a necessary but not sufficient condition. A free electron should be a free electron in all relativistic frames. Any two states of a.free elementary particle should be connectible by a transformation in the Poincare group. Thus all its states are representable by superposition of states obtained by relativistic transformations of a single state. In other words,there must be no relativistically invariant subspaces for the state space of a free elementary particle, otherwise we would call the invariant subspaces elementary. The state space of a free elementary particle is the Hilbert space for an irreducible representation of the Poincare group. Wigner had worked out the irreducible representations of the Poincare group. The group-theoretic analysis shows there are two characteristics that are invariant under relativistic transformations. These characteristics are identified as the mass m and spin s. The spin is the angular momentum in the restframe, it determines the number of linearly independent states that have the same momentum four-vector. To each (m, s) there corresponds only one irre-ducible representation up to unitary equivalence. The masses of the particle can be zero or positive; the values of the finite masses are not determined byrelativistic invariance. If a particle has finite mass, then s can be 0, 5, 1, or|, . . . . If the mass is zero, the spin is either 1 or 2. Neglecting dynamical effects, the general conceptual framework for the kinematic characteristics of types of free particles can be obtained from spatio-temporal invariance. Thus pure relativistic considerations single out mass and spin as indices for the classification of various free elementary particles and put certain constraints on their values. The specific mass and spin values for a particular species of particles must be determined empirically.

From "How is Quantum Field Theory possible" by Auyang

Why is it interesting?

Elementary particles are the fundamental building blocks and also responsible for the fundamental interactions like electromagnetism.

FAQ

How large is an elementary particle?

See https://axelmaas.blogspot.de/2018/02/how-large-is-elementary-particle.html?m=1

Why do physicists believe that particles are pointlike?

see https://physics.stackexchange.com/questions/41676/why-do-physicists-believe-that-particles-are-pointlike

History

Gell-Mann’s version of the Eightfold Way had predicted that the pro-ton, the neutron, and all the other thus-far observed strongly interactingparticles could in principle be made out of three smaller subparticlescalled quarks. Quarks, if they existed, had to be almost unbelievablypeculiar; they had to carry a fractional electric charge of either one-third or two-thirds the charge of the proton, but no one had ever seena particle of fractional charge. Although the Eightfold Way impliedtheir existence, physicists were reluctant to take them seriously. Instead,avoiding the reality behind their mathematics, they had come to thinkof quarks as mathematically consistent but fictitious components thatcould never be observed. It was as though the only coins you had everseen in circulation were nickels, dimes, and quarters, and you had con-cluded that somewhere there had to be a one-cent coin. If a proton really contained three hard little quarks deep inside it, oneshould be able to “see” them experimentally by shooting a fast electronat a proton and observing it recoil sharply when it struck a quark head-on.The method is a little like looking for bits of eggshell in a spongecake—once in a while, as you chew, you hear a sharp crack as your teethhit a fragment of shell. Robert Hofstadter, my cousin’s City College friend of the 1930s, hadobserved no such sharp recoils, and everyone had concluded that theproton was pure sponge and no eggshell. Hofstadter’s experiments, how-ever, were limited. He had kept an eye only on the so-called elasticcollisions, those in which the target proton remained intact as it recoiledlike a struck billiard ball. Now, in the late 1960s, a later generation ofphysicists at the Stanford Linear Accelerator Center (SLAC) began towatch so-called inelastic electron-proton collisions in which the protondisintegrated rather than recoiled after being struck. Amazingly, in thesecollisions, many of the electrons did in fact recoil sharply, as though theyhad struck something very hard and small. Somewhere deep inside theretruly were bits of eggshell.

From My Life As A Quant by Emanuel Derman