Add a new page:
see also Lagrangian Formalism
In Lagrangian mechanics we derive how a particle will evolve using the idea that ‘total amount that happened’ from one moment to another as a particle traces out a path is minimal.
So formulated differently, the basic idea is that nature is lazy. All we have to do is find the laziest way to realize something and this is exactly how nature will behave.
In Lagrangian mechanics we define a quantity \begin{equation} L\equiv K(t)-V(q(t)) \end{equation} called the Lagrangian. In addition, for any trajectory $q$ with $q(t_0)=a$, $q(t_1)=b$, we we define the corresponding action \begin{equation} S(q)\equiv \int_{t_0}^{t_1}L(t)\,dt. \end{equation}
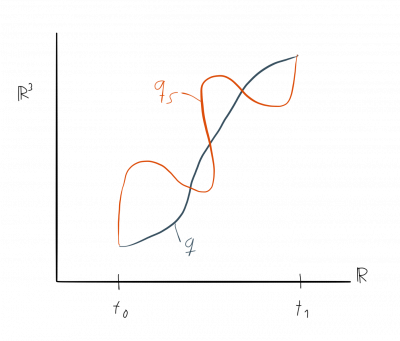
The basic idea is now that nature causes particles to follow the trajectories with the least amount of action.
In the image on the right-hand side this could be the solid line denotes by $q$. Another path is shown as a dashed line and denoted by $q(s)$.
The Lagrangian approach assigns to each path a quantity called action as defined above and then tells us that the correct path that an object really follows is the path with minimal action. In our example the path $q$ could have an action of $3$ and the path $q_s$ an action of $5$. Hence, path $q$ is correct and not path $q_s$.
The mathematical toolset that we use to find the paths with minima action is known as variational calculus.
The final result using this machinery is that the path with minimal action is the one that satisfies the Euler-Lagrange equations.
Using the Lagrangian approach, we can derive Newtonian mechanics. Alternatively, we can start with Newtonian mechanics and derive Lagrangian mechanics.
Examples
$$ \cal L=T-U . $$
Therefore, a harmonic oscillator in the Lagrangian framework is characterized by the action
$$ S = \int dt \left( \frac{m}{2} \left(\frac{dx}{dt}\right) - \frac{k}{2}x^2 \right) ,$$ where $L= \frac{m}{2} \left(\frac{dx}{dt}\right) - \frac{k}{2}x^2$ is the Lagrangian.
Starting from this action, we can derive the equation of motion by using the Euler-Lagrange equation.
$$ \frac{\partial {\cal L}}{\partial x}-\frac{d}{dt}(\frac{\partial {\cal L}}{\partial dot{x}})= 0 $$
$$ \Rightarrow m \frac{d^2}{dt^2} x -kx= 0$$
Small Amplitude Approximation
If $\theta <<1$ then $\sin\theta\approx\theta$ and \[\frac{d^2\theta}{dt^2}+\frac{g}{r}\theta\] This solution describes simple harmonic motion \[\theta=A\cos(\omega t-\phi)\] where \[\omega=\sqrt{\frac{g}{r}}\] and the constants $A$ and $\phi$ are determined from the initial condition E.g. if $\theta=0,\;t=0$ then $\phi=\pm \frac{\pi}{2}$. If $d\theta/dt=0,\;t=0$ then $\phi=0,$ or $\pi$ (depending on whether the pendulum is moving to the left or right initially) The period is \[\tau=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{r}{g}}\]
Finite Amplitude
If the amplitude is not small we have to solve the nonlinear equation \[\frac{d^2\theta}{dt^2}+\frac{g}{r}\sin \theta=0\] (nonlinear because sin $\theta$ is a nonlinear function of the dependent variable $\theta$.)
We have \begin{align*} K &= \frac{1}{2}(m_1+m_2)(\frac{d}{dt}(\ell-x))^2 = \frac{1}{2}(m_1+m_2)\dot{x}^2 \\ V &= -m_1 g x - m_2 g(\ell-x) \\ \text{so } L &= K-V = \frac{1}{2}(m_1+m_2)\dot{x}^2 + m_1gx+m_2g(\ell-x) \end{align*} The configuration space is $Q=(0,\ell)$, and $x\in(0,\ell)$. Moreover $TQ=(0,\ell)\times\mathbb{R}\ni(x,\dot{x})$. As usual $L:TQ\rightarrow\mathbb{R}$. Note that solutions of the Euler-Lagrange equations will only be defined for \emph{some} time $t\in\mathbb{R}$, as eventually the solutions reaches the ``edge'' of $Q$.
The momentum is: \[ p = \frac{\partial L}{\partial\dot{x}} = (m_1+m_2)\dot{x} \] and the force is: \[ F = \frac{\partial L}{\partial x} = (m_1-m_2)g \] The Euler-Lagrange equations say \begin{align*} \dot{p} &= F \\ (m_1+m_2)\ddot{x} &= (m_1-m_2)g \\ \ddot{x} &= \frac{m_1-m_2}{m_1+m_2}g \end{align*} So this is like a falling object in a downwards gravitational acceleration $a=\left(\frac{m_1-m_2}{m_1+m_2}\right)g$.
We integrate the expression for $\ddot{x}$ twice to obtain the general solution to the motion $x(t)$. Note that $\ddot{x}=0$ when $m_1=m_2$, and $\ddot{x}=g$ if $m_2=0$.
Reading Recommendations
Lagrangian mechanics can be formulated geometrically using fibre bundles.
The Lagrangian function is defined on the tangent bundle $T(C)$ of the configuration space $C$.
In contrast, the Hamiltonian function is defined on the cotangent bundle $T^\star(C)$, which is also called phase space.
The map from $T^\star(C) \leftrightarrow T(C)$ is called Legendre transformation.