Intuitive

The adjoint representation describes how the generators of the group, which live in the Lie algebra, transform. In other words, the adjoint representation acts on the Lie algebra. Note that the Lie algebra is a vector space and thus can serve as a representation space.

The dimensionality of the adjoint representation is equal to that of the Lie algebra. For example, the adjoint representation of $SU(2)$ is 3 dimensional and the adjoint representation of $SU(3)$ is 8 dimensional.

An important application of the adjoint representation is the transformation of gauge fields.

Concrete

• For a detailed discussion, see What’s so special about the adjoint representation of a Lie group? by J. Schwichtenberg

Example

The diagram below shows the defining representation of $SU(2)$ in its upper branch. To construct the adjoint representation, we use the Lie algebra as the representation space, as shown in the lower branch (red arrows). The group elements act on this space like $L'=ULU^{-1}$ and the Lie-algebra elements act like $L'=[J,L]$. It is possible to rewrite the adjoint representation such that it acts on 3-dimensional vectors (as opposed to 2x2 matrices) by regular matrix-vector multiplication.

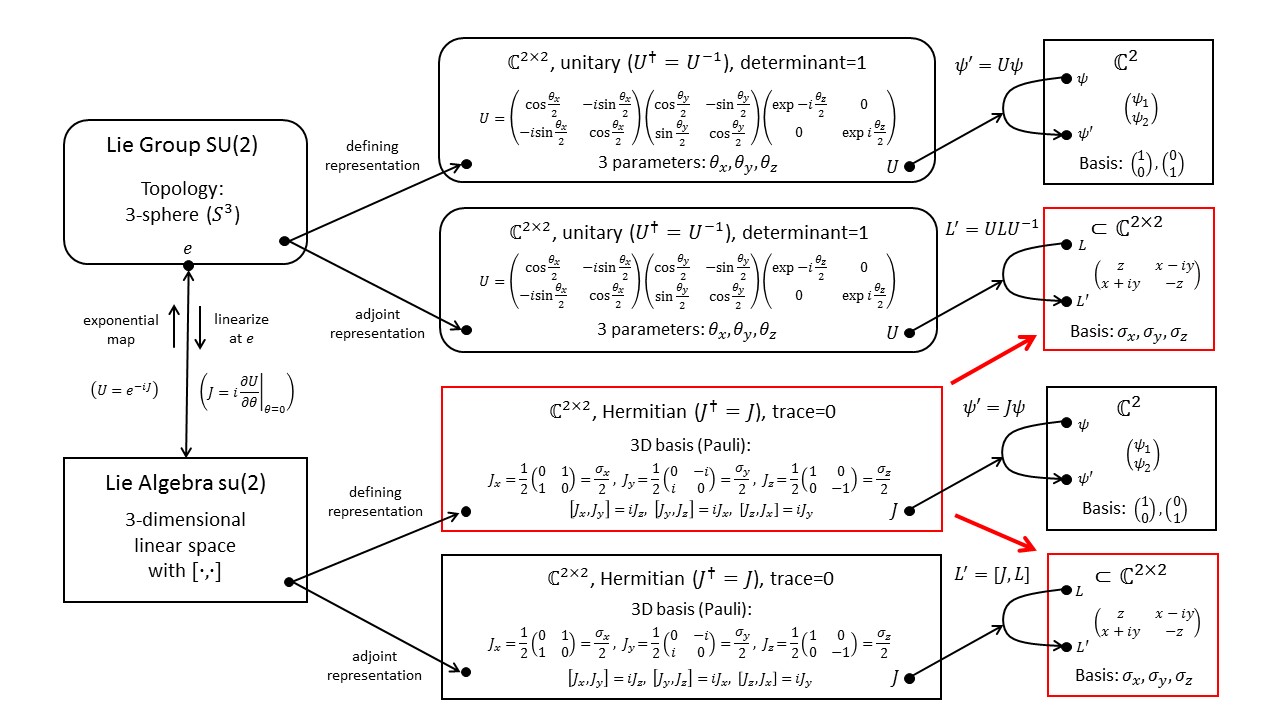
For a more detailed explanation of this diagram as well as adjoint representations of other groups, see Fun with Symmetry.

Abstract

Why is it interesting?

A representation is a map that maps each element of the set of abstract groups element to a matrix that acts on a vector space. A confusing point here is: If we can study the representation of any group on any vector space, where should we start?

Luckily there comes exactly only distinguished vector space automatically with each Lie group: the Lie algebra of the group!

The representation of each group where it acts on its own Lie algebra is called the adjoint representation.