Intuitive

The Lie algebras consist of infinitesimally small transformations and are used in physics to describe symmetries. Since arbitrarily large continuous transformations can be built up from tiny ones, almost everything that is important about continuous transformations is encoded in the infinitesimal ones.

Formulated differently, Lie algebras describe infinitesimal symmetries.

Concrete

Lie groups describe continuous symmetries. Therefore, we can consider group elements that are arbitrarily close to the identity element. In mathematical terms, we denote a transformation really close to the identity element (which changes nothing at all) by $$ g(\epsilon) = I + \epsilon X,$$ where $\epsilon$ is, as usual, a small number and $X$ is called a generator for reasons that will become clear in a moment.

When this small transformation $g(\epsilon)$ acts on an object it barely changes anything. Nevertheless, we can repeat such a tiny transformation many, many times to get a large transformation. For example, many small rotations yield a large rotation.

In mathematical terms, this idea of repeating our small transformation many times can be expressed as \begin{equation} h(\theta)=(I+ \epsilon X) (I+ \epsilon X) (I+ \epsilon X) \ldots = (I+ \epsilon X) ^k \, , \end{equation} where $k$ denotes how often we repeat the tiny transformation.

Now the idea is that if we have a finite transformation, say a rotation by $\theta= 50^\circ$, we can describe this through the repetition of an infinitesimal (= tiny tiny tiny) transformation. Everything important about the finite transformation is encoded in the infinitesimal transformation.

To realize this idea explicitly, we divide $\theta$ by a large number $N$ in order to make sure that we are close to the identity. This means, our transformation close to the identity transformation is now written as

\begin{equation} g(\theta)=I+ \frac{\theta}{N} X .\end{equation}

Now, if are interested in the objects that are as close as possible to the identity element, we must consider the limit $N \rightarrow \infty$. At the same time, when we want to get a finite transformation from such a tiny transformation, we must repeat it infinitely often: \begin{equation} h(\theta)= \lim_{N \rightarrow \infty} (I+ \frac{\theta}{N} X) ^N \, .\end{equation}

In the limit $N \rightarrow \infty$ this is exactly the exponential function.

\begin{equation} h(\theta)= \lim_{N \rightarrow \infty} (I+ \frac{\theta}{N} X) ^N = e^{\theta X} \, .\end{equation}

We can now see that it makes sense to say that the mysterious object $X$ generates the finite transformation $h$. This is why $X$ is called a generator.

For different transformations, for example, rotations around different axes, we have different generators. The set of all generators is the Lie algebra of the group. With the line of thought from above we can now understand how the Lie algebra is the tangent space above the identity.

There is another way to look at the Lie algebra of a given group, that makes use of the Taylor series. The Taylor series of a function $h(\theta)$ is \begin{equation} h(\theta)=I+ \frac{ dh}{d \theta }. |_{\theta=0} \theta + \frac{1}{2} \frac{ d^2h}{d \theta^2 }. |_{\theta=0} \theta^2 + \ldots = \sum_n \frac{1}{n !} \frac{d^n h }{d \theta^n }\big{|}_{\theta=0 } \theta^n \, .\end{equation}

We can write this more compactly, by recalling the series definition of the exponential function: \begin{equation} h(\theta)= e ^{ \frac{ dh}{d \theta }. |_{\theta=0} \theta } \equiv \sum_n \frac{1}{n !} \frac{d^n h }{d \theta^n }\big{|}_{\theta=0 } \theta^n. \end{equation}

This way, we can see the connection to the first approach \begin{equation} X = \frac{ dh}{d \theta } |_{\theta=0} \, . \end{equation}

Definition:

The Natural Product of a Lie Algebra:

A group isn't just a set of transformations. It is a set of transformations together with a binary operation $\circ$ that tells us how we can combine group elements. For matrix Lie groups $\circ$ is simply usual matrix multiplication.

Naively, one could think that we can combine Lie algebra elements simply by using $\circ$, too. However, this is not the case! In general, for two elements of the Lie algebra $X$ and $Y$, $X \circ Y$ is not an element of the Lie algebra.

The correct connection between $\circ$ and the rule that correctly connects Lie algebra elements is revealed by the famous Baker-Campbell-Hausdorff formula:

\begin{equation} \label{eq:BCH }\mathrm{e}^{X} \circ \mathrm{e}^{Y} = \mathrm{e}^{X+Y+\frac{1}{2}[X,Y]+\frac{1}{12}[X,[X,Y]]-\frac{1}{12}[Y,[X,Y]]+\ldots} \end{equation}

On the left hand side of the equation, we have two group elements that we could call, for example $h$ and $g$: $g\equiv \mathrm{e}^{X}$ and $h\equiv \mathrm{e}^{Y}$. Therefore, \begin{equation} \underbrace{g}_{\in G} \circ \underbrace{h}_{\in G}= \mathrm{e}^{X} \circ \mathrm{e}^{Y} = \underbrace{\mathrm{e}^{X+Y+\frac{1}{2}[X,Y]+\frac{1}{12}[X,[X,Y]]-\frac{1}{12}[Y,[X,Y]]+\ldots}}_{\in G} \, . \end{equation} On the right hand side there is just one element of the group. In the exponential, we can see how the Lie algebra elements $X$ and $Y$ get combined. Not simply by matrix multiplication, but through the so-called Lie bracket $[X,Y]$. For matrix Lie groups $[X,Y]$ is simply the commutator: $[X,Y]=XY-YX$, where $XY$ denote the matrix multiplication of $X$ and $Y$. We conclude that although neither $XY$ nor $YX$ are necessarily Lie algebra elements, their difference always is!

[The] Lie algebra is completely characterized by its structure constants $c^j_{kl}$.

page 93 in "Geometrical methods of mathematical physics" by Schutz

Abstract

• How is a Lie Algebra able to describe a Group?
• What Information About a Lie Group is Not Encoded in its Lie Algebra?

Why is it interesting?

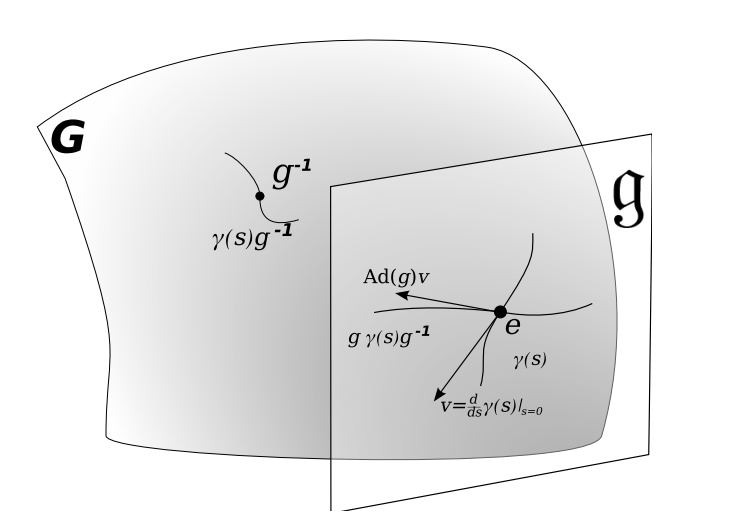
One of the most important ideas of Lie theory is that we can learn a lot about something complicated: a Lie group, by looking at something much simpler: its Lie algebra. A Lie group is a complicated mathematical object (a manifold), whereas a Lie algebra is simply a vector space. A manifold is defined as a set that looks like the good old Euclidean space in the neighborhood of every point. This tangent Euclidean space above each point can be used to define coordinates at each point. The Lie algebra $\mathfrak{g}$ of a given group $G$ is defined as the tangent space above the identity element $I$ of the group.

Experiment tells us more directly about the Lie algebra of G than about G itself. When I say that G contains the subgroup SU(3) X SU(2) x U(1), I really mean only that the Lie algebra of G contains that of SU(3) X SU(2) X U(1); there is no claim about the global form of G. For the same reason, in later comments I will not be very precise in distinguishing different groups that have the same Lie algebra.

from Geometry and Physics by E. Witten

In high-energy theory. we tend to focus on the Lie algebra of a group and ignore its global structure; for example, we indiscriminately refer to the isospin group as SU(2) or SO(3). This is an especially bad habit in monopole theory, because the quantization condition is sensitive to the global structure of G; the allowed set of monopoles is different for SU(2) and SO(3). For example, let us suppose that Q is proportional to $I_3$ , the generator of rotations about the third axis in isospin space. If G is SO(3), Q can be any half-integral multiple of $I_3$, because a rotation by $2\pi$ is the identity. If G is SU(2), though, only integral multiples are allowed, because a rotation by $4\pi$ is needed to get back to the identity.

The Magnetic Monopole Fifty Years Later by Sidney R. Coleman

[P]erturbative effects depend only on the Lie algebra.

Global structure of the standard model, anomalies, and charge quantization by Joseph Huck