Why is it interesting?

Lie groups describe continuous symmetry and lie at the heart of modern physics. For example, the symmetry group of the standard model of particle physics and the best spacetime symmetry group that we know (the Poincare group) are Lie groups.

Layman

A Lie group is a continuous set of transformations that satisfy the group axioms. A good example for a Lie group is the symmetry group of the circle. A rotation by $5^\circ$ is a symmetry of the circle and a rotation by $0.00001^\circ$ is a symmetry, too. In contrast, the symmetry group of a square is not continuous. A rotation by $90^\circ$ is a symmetry, whereas a rotation by $5^\circ$ is not a symmetry.

Student

The diagram below shows some low-dimensional, but important, Lie groups and their relationships.

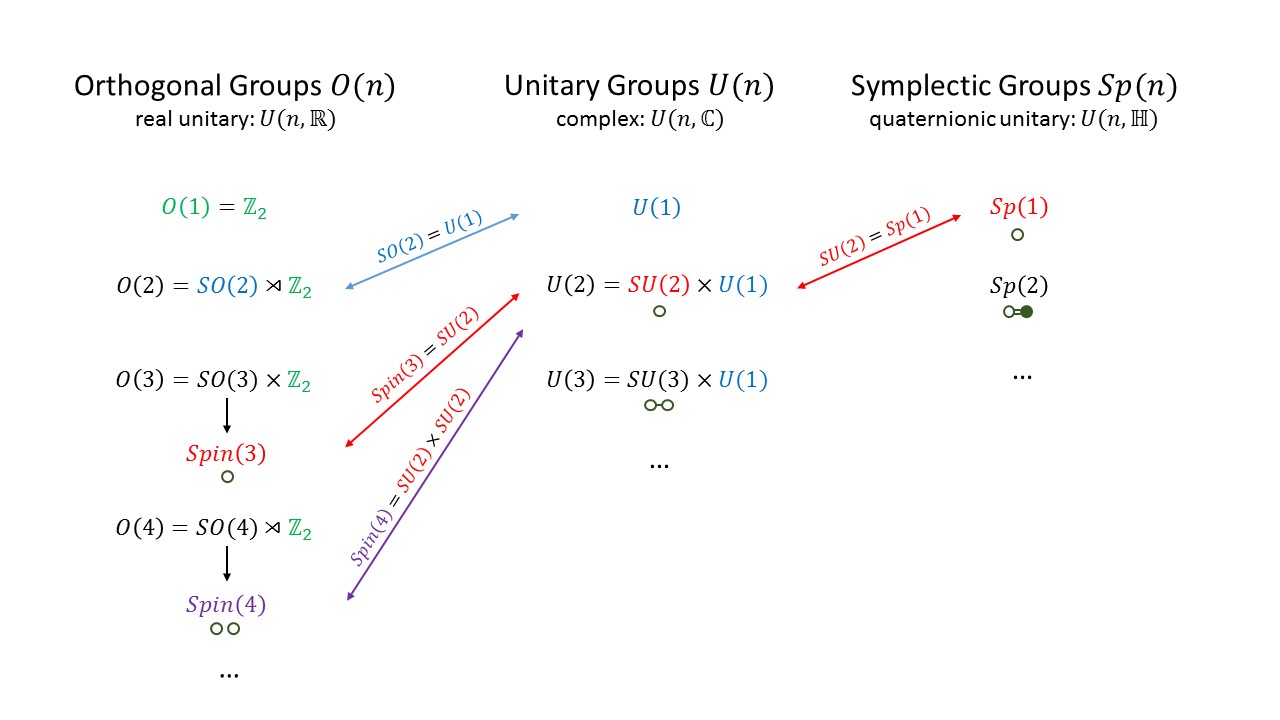
For a more detailed explanation of this diagram and much more, see Fun with Symmetry.

For book recommendations, see here.

Researcher

Examples

Example1

Example2:

FAQ

History