Intuitive

Concrete

In Lagrangian mechanics we define a quantity \begin{equation} L\equiv K(t)-V(q(t)) \end{equation} called the Lagrangian. In addition, for any trajectory $q$ with $q(t_0)=a$, $q(t_1)=b$, we we define the corresponding action \begin{equation} S(q)\equiv \int_{t_0}^{t_1}L(t)\,dt. \end{equation}

Source: Lectures on Classical Mechanics by John C. Baez

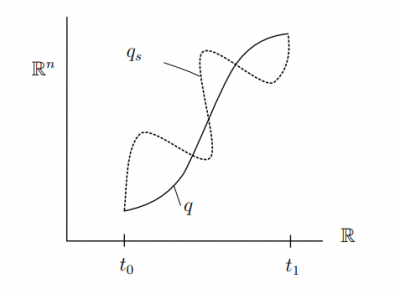
The basic idea is now that nature causes particles to follow the trajectories with the least amount of action.

In the image on the right-hand side this could be the solid line denotes by $q$. Another path is shown as a dashed line and denoted by $q(s)$. The Lagrangian approach assigns to each path a quantity called action as defined above and then tells us that the correct path that an object really follows is the path with minimal action. In our example the path $q$ could have an action of $3$ and the path $q_s$ an action of $5$. Hence, path $q$ is correct and not path $q_s$.

The mathematical toolset that we use to find the paths with minima action is known as variational calculus.

Using the Lagrangian approach, we can derive Newtonian mechanics. Alternatively, we can start with Newtonian mechanics and derive Lagrangian mechanics.

Derivation of Newton's second law

A point with minimal action is $S$ defined through the condition \begin{equation} \left. \frac{d}{ds}S(q_s)\right|_{s=0} = 0 \end{equation} where \[ q_s = q + s\delta q \] for all $\delta q \colon [t_0,t_1]\rightarrow\mathbb{R}^n$ with \[ \delta q(t_0)=\delta q(t_1)=0. \] We want to derive \begin{equation} F=ma \quad \Leftrightarrow \quad \left.\frac{d}{ds} S(q_s)\right|_{s=0}=0 \; \textrm{for all} \; \delta q\colon [t_0,t_1]\rightarrow\mathbb{R}^n \; \textrm{with}\; \delta q(t_0)=\delta q(t_1)=0. \end{equation} To do this, we now use the definition of the action and the chain rule: \[ \begin{split} \left.\frac{d}{ds}S(q_s)\right|_{s=0} &= \frac{d}{ds}\left.\int_{t_0}^{t_1} \frac{1}{2}m\dot{q}_s(t)\cdot\dot{q}_s(t)-V(q_s(t))\,dt\right|_{s=0} \\ \\ &= \left.\int_{t_0}^{t_1}\frac{d}{ds}\left[ \frac{1}{2}m\dot{q}_s(t) \cdot \dot{q}_s(t) - V(q_s(t))\right]dt\right|_{s=0} \\ \\ &= \left.\int_{t_0}^{t_1}\left[ m\dot{q}_s \cdot \frac{d}{ds}\dot{q}_s(t)- \nabla V(q_s(t)) \cdot \frac{d}{ds}q_s(t)\right]dt\right|_{s=0} \\ \end{split} \] Next we note that \[ \frac{d}{ds} q_s (t) = \delta q(t) \] so \[ \frac{d}{ds} \dot{q}_s (t) = \frac{d}{ds} \frac{d}{dt} {q}_s (t) = \frac{d}{dt} \frac{d}{ds} {q}_s (t) = \frac{d}{dt} \delta{q}(t) .\] Therefore we have \[ \begin{split} \left.\frac{d}{ds}S(q_s)\right|_{s=0} &= \int_{t_0}^{t_1}\left[ m\dot{q} \cdot \frac{d}{dt} \delta q(t) - \nabla V(q(t)) \cdot \delta q(t)\right]dt . \end{split} \] Finally, we can integrate by parts and note that the boundary terms vanish because $\delta q=0$ at $t_1$ and $t_0$: \[ \begin{split} \frac{d}{ds}S(q_s)\rvert_{s=0} &= \left.\int_{t_0}^{t_1}\left[ -m\ddot{q}(t)-\nabla V(q(t))\right] \cdot \delta q(t) dt\right. . \\ \end{split} \] Looking at this, we can see that the variation of the action vanishes for all possible variations $\delta q$ if and only if the term in brackets is exactly zero: \[ -m\ddot{q}(t)-\nabla V(q(t)) = 0. \] Therefore, the correct path $q$ with a minimal amount of action $S$ is the one that follows from the equation \[ F=ma. \]

Abstract

Lagrangian mechanics can be formulated geometrically using fibre bundles.

The Lagrangian function is defined on the tangent bundle $T(C)$ of the configuration space $C$.

In contrast, the Hamiltonian function is defined on the cotangent bundle $T^\star(C)$, which is also called phase space.

The map from $T^\star(C) \leftrightarrow T(C)$ is called Legendre transformation.

• See page 471 in Road to Reality by R. Penrose, page 167 in Geometric Methods of Mathematical Physics by B. Schutz and http://philsci-archive.pitt.edu/2362/1/Part1ButterfForBub.pdf.

Why is it interesting?