Intuitive

It turns out that the abstract phase fluid has the same properties as a real fluid that is incompressible. An incompressible real fluid is one in which any volume-element of fluid (any sample of neighbouring ‘particles’) cannot be compressed, that is, it keeps the same volume. Likewise, for the phase fluid we may examine any small 2n-dimensional volume-element within the fluid, and watch this volume as it is ‘carried along’ by the flow. Although the shape of the volume-element may become distorted yet its total volume always remains unchanged.

The Lazy Universe by Coopersmith

Liouville's theorem can be thought of as conservation of information in classical mechanics.

Suppose you have a bowl, perhaps of some slightly-wonky shape, and a marble that can roll around in the bowl. You put the marble down somewhere and give it a push. (We'll call the this the initial state.) The marble does its thing. Using physics, you can predict where it will be and how fast it will be going 10 seconds from now. (We'll call this the final state.)

However, you might not know the initial state perfectly. Instead there is some range of possible initial states. The size of the range of initial states represents your uncertainty.

Due to the uncertainty, you can't calculate the exact final state. Instead, there is uncertainty about the final state. Liouville's theorem says that you have the same amount of uncertainty about the initial and final states.

The size of the uncertainty is a measure of how much information you have, so Liouville's theorem says that you neither gain nor lose information, i.e. information is conserved. (Specifically, the information you have is the negative of the logarithm of the uncertainty.) http://qr.ae/TU1ODq

But all physical measurements have a definite limitation on how accurately they can be performed, and can only give information about a finite number of decimal places. […] What this means, in terms of phase space, is that each of our 'discrete' alternatives must correspond to a region in phase space, so that different phase-space points lying in the same region would correspond to the same one of these alternatives for our device (Fig. 5.12)

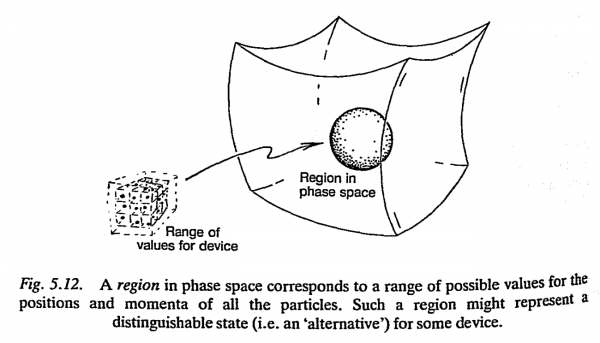
Now suppose that the device starts off with its phase-space point in some region Ro corresponding to a pal ticular one of these alternatives. We think ~f Ro as being dragged along the Hamiltonian vector field as time proceeds, until at time t the region becomes $R_t$. In picturing this, we are imagining simultaneously, the time-evolution of our system for all possible starting states corresponding to this same alternative. (See Fig. 5.13.) The question of stability (in the sense we are interested in here) is whether, as t increases, the region $R_t$ remains localized or whether it begins to spread out over the pase space. If such regions remain localized as time progresses, then we have a measure of stability for our system. Points of phase space which are close together (so that they correspond to detailed physical states of the system which closely resemble one another) will remain close together in phase space, and inaccuracies in their specification will not become magnified with time. Any undue spreading would entail an effective unpredictability in the behaviour of the system.

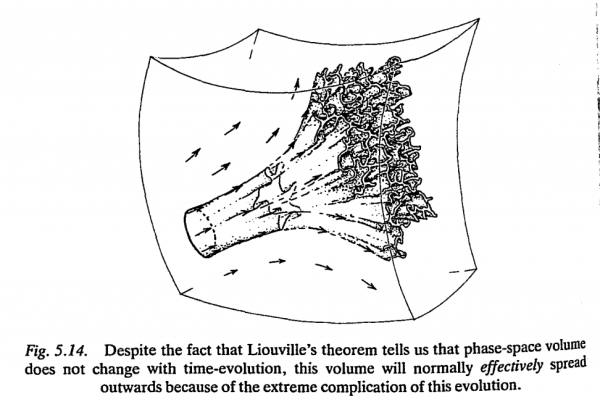
What can be said about Hamiltonian systems generally? Do regions in phase space tend to spread with time or do they not? It might seem that for a problem of such generality, very little could be said. However, it turns out that there is a very beautiful theorem, due to the distinguished French mathematician Joseph Liouville (1809-1882), that tells us that the volume of any region of the phase space must remain constant under any evolution. At first sight this would seems to answer our stability question in the affirmative. For the size - in the sense of this phase space volume - of our region cannot grow, so it would seem that our region cannot spread itself out over the phase space. However this is deceptive, and on reflection we see that the very reverse is likely to be the case!

[…]

The volume indeed remains the same, but this same small volume can get very thinly spread out over huge regions of the phase space. For a somewhat analogous situation, think of a small drop of ink placed in a large container of water. Whereas the actual volume of material in the ink remains unchanged, it eventually becomes thinly spread over the entire contents of the container. […] The trouble is that preservation of volume does not at all imply preservation of shape: small regions will tend to get distorted, and this distortion gets magnified over large distances.

[…]

In fact, far from being a 'help', in keeping the region $R_t$ under control, Liouville's theorem actually presents us with a fundamental problem! Without Liouville's theorem, one might envisage that this undoubted tendency for a region to spread our in phase space could, in suitable circumstances, be compensated by a reduction in overall volume. However, the theorem tells us that this is impossible, and we have to face up to this striking implication - a universal feature of all classical dynamical (Hamiltonian) systems of normal type!

We may ask, in view of this spreading throughout phase space, how is it possible at all to make predictions in classical mechanics? That is, in indeed, a good question. What this spreading tells us is that, no matter how accurately we know the initial state of a system (within some reasonable limits), the uncertainties will tend to grow in time and our initial information may become almost useless. Classical mechanics is, in this kind of sense, essentially unpredictable.

How is it, then, that Newtonian dynamics has been seen to be so successful? In the case of celestial mechanics (o.e. the motion of heavenly bodies under gravity), the reasons seem to be, first, the one is concerned with a comparatively small number of coherent bodies (the sun, planets, and moons) which are greatly segregated with regard to mass- so that to a first approximation one can ignore the perturbing effect of the less massive bodies and treat the larger ones as just a few bodies acting under each other's influence- and, second, that the dynamical laws that apply to the individual particles which constitutes those bodies can be seen also to operate at the level of the bodies themselves- so that to a very good approximation, the sun, planets, and moons can themselves be actually treated as particles, and we do not have to worry about all the little detailed motions of the individual particles that actually compose these heavenly bodies. Again we get away with considering just a "few" bodies, and the spread in phase space is not important.

[…]

This spreading effect in phase space has another remarkable implication. It tells us, in effect, that classical mechanics cannot actually be true of our world!

[…]

As we now know, quantum theory is needed in order that the actual structure of solids can be properly understood. Somehow, quantum effects can prevent this phase-space spreading. This is an important issue to which we shall have to return later (see Chapters 8 and 9)

page 174ff in "The Emperors new Mind" by R. Penrose

It turns out that the abstract phase fluid has the same proper- ties as a real fluid that is incompressible. An incompressible real fluid is one in which any volume-element of fluid (any sample of neighbouring ‘particles’) cannot be compressed, that is, it keeps the same volume. Likewise, for the phase fluid we may examine any small 2n-dimensional volume-element within the fluid, and watch this volume as it is ‘carried along’ by the flow. Although the shape of the volume-element may become distorted yet its total volume always remains unchanged:The Lazy Universe by Coopersmith

Concrete

Liouville's theorem tells us that the flow of the probability density $\rho(t,\vec p,\vec q)$ is incompressible. The probability density is a non-negative real quantity that tells us the probability that we'll find a particle with momentum $\vec p$ at the position $\vec q$.

In general, for a function $\rho(t,\vec p,\vec q)$ we have

$$ \frac{\mathrm d}{\mathrm dt} \rho(t, \vec p(t), \vec q(t)) =\frac{\partial \rho }{\partial t}+ \sum_{i}\left(\frac{\partial \rho}{\partial q_i}\,\dot{q_i}+\frac{\partial\rho}{\partial p_i}\,\dot p_i\right) . $$

Now, if $\rho$ is constant $\frac{d \rho }{d t}= 0$, then the left-hand side is $0$ and we get:

$$\frac{\partial \rho }{\partial t}= -\sum_{i}\left(\frac{\partial \rho}{\partial q_i}\,\dot{q_i}+\frac{\partial\rho}{\partial p_i}\,\dot p_i\right).$$

This is a dynamical equation for the time-evolution of $\rho(t,\vec p,\vec q)$ that follows when the flow of the probability density $\rho(t,\vec p,\vec q)$ is incompressible, i.e. $\frac{d \rho }{d t}= 0$.

Take note that Liouville's theorem can be violated by any of the following:

• sources or sinks of particles;
• existence of collisional, dissipative, or other forces causing $\nabla_{\mathbf{p}}$ $\cdot$ $\mathbf{F}$ $\neq$ 0;
• boundaries which lead to particle trapping or exclusion, so that only parts of a distribution can be mapped from one point to another;
• spatial inhomogeneities that lead to velocity filtering (e.g., particle drift velocities that prevent particles with smaller velocities from reaching the location they would have reached had they not drifted);
• temporal variability at source or elsewhere which leads to non-simultaneous observation of oppositely-directed trajectories;
• etc. [_Paschmann and Daly_ 1998].

Abstract

The intuition for the Lagrangian principle comes specific applications of Newton's laws, especially reversible systems with constraints, like nonspherical particles rolling along complicated surfaces. Newton's formulation of Newton's laws was not the end of the story, because there was more structure in the solutions of these types of problems than that which Newton made obvious.

One thing left unsaid by Newton is conservation of energy. Elastic processes are more fundamental than inelastic ones. But energy conservation is only part of the story. Suppose you have a bunch of masses connected by springs, and one of them is attached to a double-pendulum. You could theoretically have energy conservation in such a system by having all the energy leak out of the masses on the springs and go into the double pendulum. Perhaps every frictionless motion of the springs eventually settles all the energy into a single mode.

Your intuition is probably rebelling, telling you "that's infinitely unlikely! How could the pendulum move around and not set the springs vibrating!" But there is nothing in Newton's laws by themselves, even with the principle of conservation of energy, that prevents this sort of concentration of energy. But the solutions do not exhibit such phenomena, and there must be a reason why.

This intuition tells you that a perfect frictionless mechanical system is more than energy-conserving, it must conserve some notion of "motion-volume", so that if you alter the initial state by a certain amount, the final state should alter the same way. It can't concentrate all motion into one mode. This principle is the principle of conservation of phase-space volume, or the conservation of information. If all the motion got concentrated into one mode, the information about where everything was would have to get absurdly compressed into a tiny region of the phase space, the space of all possible motions.

The conservation of information is just about as fundamental as Newton's laws of motion— it is revealing new facts about nature which are essential for the description of statistical and quantum systems. But it is nowhere to be found in Newton's formulation, because it does not follow from Newton's laws alone, even with the principle of conservation of energy added.

So you need to understand what type of law will give a law of conservation of information. There are two paths to go down, and both lead to the same structure, but from two different points of view, local in time and global in time.

One path is Hamiltonian: you consider formulating the law of motion as a set of symplectic equations for the position and momentum. This formulation clearly separates between reversible and irreversible dynamics, because it only works for reversible. It also explains the fundamental mathematical structure behind reversible classical mechanics, the symplectic geometry. The volume of symplectic geometry gives the precise law of information conservation, and further, the geometrical structure of systems with multiperiodic solutions, the integrable systems, is made clear.

But this point of view is centered on a time-slicing— it describes things going from one instant of time to another. This is not playing very nice with relativity. So you also want to think about the solution globally, and consider the space of all solutions as the phase space. The initial position and velocities are good coordinates, and intuitive ones, because they determine the future. But if you want a global picture, you want coordinates which are symmetric between the final and initial state, since the dynamics are reversible. An explicit revesible description should treat the initial time and final time symmetrically. So you can use the initial positions and final positions, which also, generically, away from certain bad choices, determine the motion.

For these types of coordinates on phase space, you give the dynamical law as a condition on the trajectory between the intial and final positions. The condition should not be stated as a differential equation, because such a description is unnatural for boundary conditions of this sort. But when you have an action principle, you determine the trajectory by extremizing the action between the end points, you automatically have a notion of phase space volume, which is intuitive— the phase space volume is defined by the change in the action of extremal trajectories with respect to changes in the initial velocities. This volume is the same as for the changes of the extremal trajectories with respect to changes in the final velocities. This is a straightforward consequence of the equivalence of Lagrangian and Hamiltonian formulation.

The full justification for both principles comes only with quantum mechanics. There you learn that the least action principle is a geometric optics Fermat principle for matter waves, and it is saying that the trajectories are perpendicular to constant-phase lines. But historically, the Lagrangian formulation was recognized to be more fundamental a century before Hamilton conjectured that classical mechanics was a wave mechanics, and this was many decades before Schrodinger. Still, with our modern point of view, it does not hurt to learn the quantum version of these formulations first, and it certainly provides a more solid motivation than the heuristic considerations I gave above.

https://physics.stackexchange.com/a/15958/37286

Why is it interesting?

FAQ

What's the connection between Liouville's theorem and Heisenberg's uncertainty principle?

The central idea of Liouville’s theorem – that volume of phase space is constant – is somewhat reminiscent of quantum mechanics. Indeed, this is the first of several occasions where we shall see ideas of quantum physics creeping into the classical world. Suppose we have a system of particles distributed randomly within a square $\Delta q \Delta p$ in phase space. Liouville’s theorem implies that if we evolve the system in any Hamiltonian manner, we can cut down the spread of positions of the particles only at the cost of increasing the spread of momentum. We’re reminded strongly of Heisenberg’s uncertainty relation, which is also written $\Delta q \Delta p=$ constant. While Liouville and Heisenberg seem to be talking the same language, there are very profound differences between them. The distribution in the classical picture reflects our ignorance of the system rather than any intrinsic uncertainty. This is perhaps best illustrated by the fact that we can evade Liouville’s theorem in a real system! The crucial point is that a system of classical particles is really described by collection of points in phase space rather than a continuous distribution $\rho(q, p)$ as we modelled it above. This means that if we’re clever we can evolve the system with a Hamiltonian so that the points get closer together, while the spaces between the points get pushed away. A method for achieving this is known as stochastic cooling and is an important part of particle collider technology. In 1984 van der Meer won the the Nobel prize for pioneering this method.http://www.damtp.cam.ac.uk/user/tong/dynamics/four.pdf

Does Liouville's theorem apply to real systems?

No!

This is perhaps best illustrated by the fact that we can evade Liouville’s theorem in a real system! The crucial point is that a system of classical particles is really described by a collection of points in phase space rather than a continuous distribution $\rho(q, p)$ as we modeled it above. This means that if we’re clever we can evolve the system with a Hamiltonian so that the points get closer together, while the spaces between the points get pushed away. A method for achieving this is known as stochastic cooling and is an important part of particle collider technology. In 1984 van der Meer won the the Nobel prize for pioneering this method.http://www.damtp.cam.ac.uk/user/tong/dynamics/four.pdf