Add a new page:
$ \mathcal{L} = \frac{1}{2} \left( (\partial_\mu \phi)^2 \right) - (1-cos \phi) $
The Sine-Gordon model describes a coupled set of pendulums that hang from a common support rod.
This system is the easiest system where something very non-trivial can happen.
Usually, when we think of waves we have something like in the following image in mind:

One pendulum gets pushed a little and since neighboring pendulums are coupled other pendulums also will start to swing. As a result, a wave travels through the system of pendulums.
Now, there can also be another type of non-trivial configuration of the system that is less common. We can pick one end of the support rod and twist it by $360^\circ$ while keeping the other end fixed. As a result, we get a twist in the system of pendulums as shown in the following image:
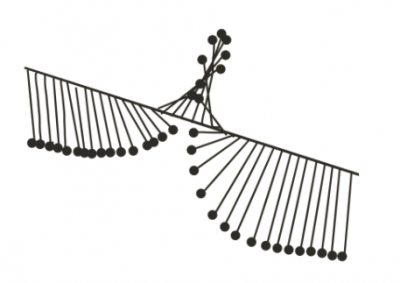
This twist is stable and just sits there as long as we don't do anything. In other words: the twist does not travel, it is stationary. In addition, the twist is stable. The field cannot relax back to the untwisted state since to do this it would need to move all pendulums and since needs too much energy. Such a field configuration is called a soliton.
It becomes important when we study how waves of the usual type travel through our system. The twist is like a barrier where usual waves get reflected. Hence, to fully understand a system like the system of pendulums here, we need to take into account that there can be twists. The most general ground state is not simply the state where all pendulums just hang downwards. This is only the naive ground state. However, the equations that describe the system also permit the twisted configurations and therefore they can appear in nature and must be taken into account.
Specification of the Model
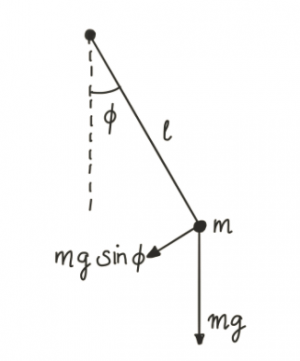
The Sine-Gordon model describes a continuous set of pendulums. Each pendulum hangs freely in a uniform gravitational field of strength $g$ on a rod with length $l$. The excitation above the ground state is measured by the angle $\phi$. At the end of the pendulum, we have a bob of mass $m$. This is shown in the picture on the right-hand side.
The Lagrangian of the system is
$$ L = \frac{1}{2} ml^2\dot{\phi}^2 - mgl (1-cos \phi), $$ where $\dot{\phi}\equiv d\phi /dt $ denotes the time derivative.
To analyze the system it is convenient to rescale the units such that all constants $m,g,l$ are equal to one. Then, the Lagrangian reads
$$ L = \frac{1}{2} \dot{\phi}^2 - (1-cos \phi). $$
So far, this could be a normal mechanics problem. However, if $\phi$ becomes not only a variable that depends on $\phi = \phi(t)$, but also on the location $\phi(t,x)$ we have a continuous set of such pendulums and hence are dealing with a field theory.
We assume that we have an infinite set of such pendulums that hang from an also infinitely long support rod.
The thing is now that neighboring pendulums are coupled to each other. This could be achieved, for example, through elastic bands between the pendulums.
In a field theory, we are not interested in the Lagrangian but in the Lagrangian density since we are interested in what happens locally. The Lagrangian density for the Sine-Gordon field theory reads
$$ \mathscr{L} = \frac{1}{2} \left( (\partial_\mu \phi)^2 \right) - (1-cos \phi), $$ $$ = \frac{1}{2} \left( \dot{\phi}^2 - (\partial_\mu \phi)^2 \right) - (1-cos \phi).$$ where $ L = \int_{-\infty}^\infty dx\mathscr{L} $ and $\mu =0,1$.
Here $\frac{1}{2} \left( (\partial_\mu \phi)^2 \right)$ is just the usual kinetic term and $(1-cos \phi)\equiv U$ is the potential of the system.
Now that we have the Lagrangian density, we can derive the equations of motion of the system, as usual, by using the Euler-Lagrange equations
$$\frac{\partial \mathscr{L}}{\partial \Phi^i} - \partial_\mu \left(\frac{\partial \mathscr{L}}{\partial(\partial_\mu\Phi^i)}\right) = 0$$
which yields
$$ \partial_\mu \partial^\mu \phi + \sin \phi =0\, . $$
When we now want to understand what the system actually does, we must search for solutions of this field equation. Before doing that, we want to think about what kind of solutions we can except.
The ground state of the system is when all pendulums are hanging straight downwards. This is the trivial solution $\phi(x,t) =0$ and also called the vacuum solution.
However, take note that the potential $U =1-cos \phi$ is minimized not only for $\phi =0$, but also for all $\phi = 2\pi k$, for all integers $k$. Therefore, we really have an infinite number of degenerate vacua. This will become important in a moment. But first let's talk about actual dynamical stuff that can happen in the system.

Since the pendulums are coupled it is possible that waves travel through the set of pendulums. Think of a "laola wave" that travels through a sports stadium. These waves can have different amplitudes and wavelengths and really correspond to the type of waves that we are used to.
In addition, to such normal waves, we can also have solitary wave. Imagine we pick one end (at $x= -\infty$) of the support rod and rotate it by $360^\circ$. This will yield a twist in the system and as a result, a solitary wave will travel through the system.
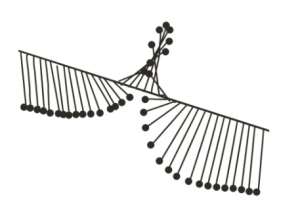
This is shown in the image on the right-hand side.
In physics, we are usually only interested in field configuration with finite energy. Hence, the field must be in a ground state configuration at infinity:
$$ V(\phi(\infty)) = V(\phi(-\infty)) \ \rightarrow \ \ \phi(\infty)\stackrel{!}{=} 2\pi k, \quad \phi(-\infty)\stackrel{!}{=} 2\pi l , $$
where $k$ and $l$ are arbitrary integers. These are the appropriate boundary conditions if we are interested in finite energy configurations.
So in the simplest case we have simply $\phi(\infty)= \phi(-\infty)=0$. In words, this means that there is no twist in the system. However, for all other possible values of the field at the boundary, we have one or more twists in the system. For example, in the example above we twisted the support rod at $x=- \infty$ once by $360^\circ = 2\pi$ and left it at $x= \infty$ as it was. This means the boundary conditions of this field configuration are
$$ \phi(\infty) = 0, \quad \phi(-\infty)= 2\pi . $$
This is what characterizes soliton. A soliton is a topological nontrivial field configuration and we can now understand why it is stable. To get rid of such a twist in the system we have to move all pendulums from $x=-\infty$ to $x = \infty$. There are infinitely many pendulums that need to be moved and hence the energy that would be required to get rid of such a twist is infinity. However, the energy stored in the twist is finite. This follows because the field configuration is in the ground state at infinity. The thing is that it is at different ground states at $x=-\infty$ to $x = \infty$.
The quantity that characterizes such twists in the system has the fitting name "winding number" and for the Sine-Gordon model we can define it as
$$ n \equiv \frac{\phi(\infty)-\phi(-\infty)}{2\pi} \in \mathbb{Z}. $$
Solitonic Solutions in Detail
Since solitons are stable and static, we now try to find such a solution of the field equations. Static means that a soliton is time-independent and therefore we can make the ansatz that our soliton solution is time independent. This yields the static Sine-Gordon equation
$$ - \partial_x \partial^x \phi + \sin \phi =0. $$
This is an ordinary 2nd-order differential equation which we can solve analytically.
Multiplying the static Sine-Gordon equation with $\partial^x \phi$ yields $$ \partial^x \phi \partial_x \partial^x \phi + = \partial^x \phi \sin \phi. $$
Now, integrating this equation yields
$$ \frac{1}{2} (\partial^x \phi)^2 = - \cos \phi +A, $$
where $A$ is the constant of integration.
Since we know that at infinity we must have $\partial^x \phi \to 0$ and $\cos \phi \to 1$ in order to have a configuration with finite energy, we can deduce $A=1$.
Now, using $\cos 2\phi = 1-\sin \phi$ and integrating yields
$$ \int_0^\phi \frac{d\phi}{\sin\frac{\phi}{2}} = \pm 2\int_{x_0}^x dx , $$
where $x_0$ denotes the location of the soliton. Perming the integration yields
$$ \ln \left( \tan \frac{\phi}{4} \right) = \pm (x -x_0) . $$ We can rewrite this as
$$ \phi(x)_k = 4\arctan \left( e^{\pm (x-x_)} \right) \tag{Eq. 1} $$
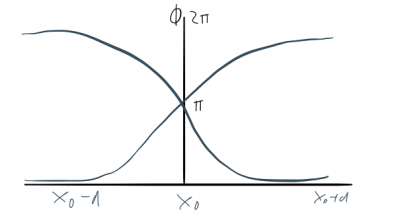
The $\pm$ in the exponent corresponds to solitons with winding number $n=\pm 1$. The solution with $n=1$ is known as the kink solution and the solution with $n=-1$ as the antikink solution.
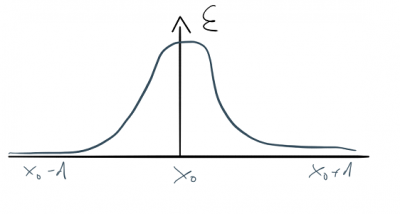
When we plot the kink solution we can see that it is a wave-packet of finite energy that is centered around $x_0$. In other words, a kink is like a potential barrier in the system.
If we now want to calculate the mass of the kink, we have to integrate the Hamiltonian density since it simply represents the energy. We get the Hamiltonian density, as usual, from the Lagrangian density and the integrated result is
$$ E[\phi] = \int_{-\infty}^\infty dx \left( \frac{1}{2} \left( (\partial_\mu \phi)^2 \right) + (1-cos \phi) \right) = \int_{-\infty}^\infty dx \left( \frac{1}{2} \left( (\partial_\mu \phi)^2 \right) + U(x) \right) $$
To get the specific energy density of the kink, we need to calculate the derivative of the solution in Eq. 1: $$ \partial_x \phi(x)_k = \frac{4}{1-e^{2(x-x_)}} = \frac{4}{e^{(x-x_)}+e^{-(x-x_)}} = 2 \text{sech}(x-x_0).$$
Putting this into the potential yields
$$ U(x) = 2 \text{sech}^2(x-x_0). $$
The total energy of the kink is therefore
$$ E[\phi_k] = 4 \int_{-\infty}^\infty dx \text{sech}^2(x-x_0) = 8. $$
Recommended Resources:
The Sine-Gordon model is dual to the massive Thirring model.
This is surprising since the Sine-Gordon model is a purely scalar theory, while the massive Thirring model is a purely fermionic theory. However, the solitons in the Sine-Gordon model are fermionic, while the solitons in the Thirring model are scalars.
| massive Thirring model | Sine-Gordon model | |
|---|---|---|
| fermions | fundamental | solitons |
| bosons | solitons | fundamental |
Explicitly this means, that although the Lagrangian of the massive Thirring model and the Sine-Gordon model look completely different, they ultimately describe the same physics. The only thing that is different is the perspective.
The duality can be shown by verifying that the currents in both theories are equal. Expressed differently, if the greens functions are equal the theories are equal.
The duality was shown by Coleman in
The Sine-Gordon model is a toy model that helps to understand fundamental notions like duality in a simplified setup.
In addition, the equations of the theory permit topological non-trivial solutions called solitons. Many basic features of such solitons can be studied in the Sine-Gordon model in a simplified setup.
The name "Sine-Gordon model" is a wordplay, because the equation of motion of the model is similar to the fa