Intuitive

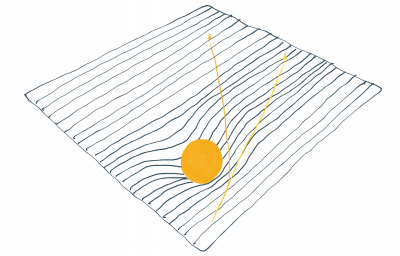The main idea of general relativity is that there is not really a gravitational force, but instead what we perceive as gravity is just a result because spacetime is curved through the presence of energy.

This means that every object transforms spacetime and all other particles which move through space roll down the slopes or up the hills that are created by all other objects.

For example, imagine a planet like our earth and a smaller object like a satellite. The heavy earth creates a depression in spacetime. As a result, the smaller satellite runs down this slope created by the earth and thus flies towards the earth's surface. (Take note that satellites can orbit around earth because the movement in a circle prevents that they fall directly onto the earth.)

• For an easy introduction to the main idea of general relativity, see http://jakobschwichtenberg.com/how-to-invent-general-relativity/

Recommended Books:

• Gravity from the ground up by Schutz
• The Perfect Theory: A Century of Geniuses and the Battle over General Relativity by Ferreira
• Kip S. Thorne, Black Holes and Time Warps: Einstein's Outrageous Legacy
• Robert M. Wald, Space, Time, and Gravity: the Theory of the Big Bang and Black Holes
• Robert Geroch, General Relativity from A to B

Concrete

Recommended Textbooks:

• A nice quick introduction can be found in Chapter 11 in Sleeping Beauties in Theoretical Physics by Thanu Padmanabhan, especially in Box 12.2
• Relativity, Gravitation and Cosmology by Ta-Pei Cheng
• Gravity by James B. Hartle
• Introducing Einstein's Relativity by R. A. D'Inverno
• A First Course in General Relativity by B. Schutz
• Einstein Gravity in a Nutshell Princeton by A. Zee
• Gravitation and Cosmology by Weinberg

Recommended Papers:

• A No-Nonsense Introduction to General Relativity by Sean M. Carroll
• The Meaning of Einstein’s Equation by John C. Baez and Emory F. Bunn
• http://people.carleton.edu/~nchriste/PTO000041.pdf
• Gravity from a particle Physicist's perspective by Percacci

The Standards Textbook:

• Gravitation by Misner Thorne Wheeler

Exercises

For exercises, see: http://phys.columbia.edu/~nicolis/G8099.html and Alan P. Lightman, William H. Press, Richard H. Price and Saul A. Teukolsky, Problem Book in Relativity and Gravitation.

Abstract

Mathematically general relativity is the study of a differential equation (the Einstein equation) satisfied by the Riemann tensor of a Lorentzian metric on a manifold.

Spacetime is a Lorentzian manifold, whereas just space is a Riemannian manifold.

So formulated a bit differently, general relativity is geometry on a Lorentzian manifold.

In general relativity, spacetime is an $(3+1)$-dimensional Lorentzian manifold. A Lorentzian manifold is a a smooth $(3+1)$-dimensional manifold $Q$ with a Lorentzian metric $g$.

The metric is defined by the conditions:

• For each $x\in Q$, we have a bilinear map \begin{align*} g(x):T_x Q\times T_x Q &\longrightarrow\mathbb{R} \\ (v,w) &\longmapsto g(x)(v,w) \end{align*} or shorter: $g(v,w)$.
• With respect to some basis of $T_x Q$ we have \begin{align*} g(v,w) &= g_{ij}v^iw^j \\ g_{ij} &=\left(\begin{array}{cccc} 1 & 0 & \ldots & 0 \\ 0 & -1 & & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \ldots & -1 \end{array}\right)\end{align*} Of course we can write $g(v,w)=g_{ij}v^iw^j$ in any basis, but for different bases $g_{ij}$ will have a different form.
• $g(x)$ varies smoothly with $x$.

Recommended Advanced Textbooks:

• Gravitation Charles W. Misner, Kip S. Thorne and John Archibald Wheeler
• General Relativity by Robert M. Wald
• Great explanations can be found in Rovelli's Quantum Gravity book. Especially on the role of general covariance in GR.
• Gravitation, Gauge Theories and Differential Geometry by Tohru Eguchi et. al.
• Principles of Relativity Physics by James L. Anderson

Why is it interesting?

General relativity is the best theory of gravity that we have. For objects with small mass its effects are approximately equal to those predicted by Newtonian gravity. However, for very massive objects like black holes, the predictions of Newtonian gravity are wrong and only general relativity is in accordance with experimental observations.

General relativity allows us to understand large-scale phenomena in our universe, such as black holes which are born when a large star collapses under its own gravitation.

The relationship of general relativity to other important classical theories is depicted nicely in the following image:

Source: http://www.pmaweb.caltech.edu/Courses/ph136/yr2012/1201.1.K.pdf

FAQ

In what sense is general relativity like the square of Yang-Mills gauge theory?

general relativity behaves like the square of Yang-Mills gauge theory [7–9]. https://arxiv.org/pdf/1704.05067.pdf

See also https://4gravitons.wordpress.com/2014/03/28/gravity-is-yang-mills-squared/?frame-nonce=109e1e5a86

The calculation involved is a little more complicated, but as discovered by Zvi Bern, John Joseph Carrasco, and Henrik Johansson, if you can get your calculation in Yang-Mills into the right format then all you need to do is square the right thing at the right step to get gravity, even for diagrams with loops! https://4gravitons.wordpress.com/2014/03/28/gravity-is-yang-mills-squared/?frame-nonce=109e1e5a86

How can we derive General Relativity?

Is it conceivable that the ‘fundamental’ interactions can be described in terms of thermodynamics? This question might sound silly; but there is already a viable example: General relativity can be derived from black hole thermodynamics. This started with the work of T. Jacobson [299], is strongly promoted by T. Padmanabhan [403], and recently was revived under the catchword ‘entropic gravity’ introduced in an article by E. Verlinde [522]. Symmetries in Fundamental Physics by K. Sundermeyer

See also: Einstein gravity as a symmetry-breaking effect in quantum field theory by Stephen L. Adler

Does curved spacetime change the volume of the space?

https://physics.stackexchange.com/questions/265071/does-curved-spacetime-change-the-volume-of-the-space

Why did it take Einstein so long to find the correct field equations?

This is answered perfectly on page 47 in the book Quantum Gravity by Rovelli.

Basically, the problem was that through the hole argument he was convinced that the correct equations cannot be generally covariant.

So what really took him so long was not finding the correct equations, but rather understanding why they work although they are generally covariant.

Can we understand General Relativity as a gauge theory?

"It is ironic that General Relativity (GR), although being historically the mother of all gauge theories, is the one whose gauge structure is the least understood. The question, "What is the gauge group of gravity?", has been raised innumerable times and has received a variety of answers that do not seem to be mutually exclusive. The Lorentz group, the Poincare group, the group of translations, and the deSitter group have all been proposed as gauge group for gravity. On the other hand, some physicists have always maintained that the gauge group of GR is the group of general coordinate transformations (or equivalently its active counter par, the group of diffeomorphisms of spacetime.) It has to be admitted that no fundamental new insight has emerged from these investigations. So the situation is quite discouraging. Yet, the question about the gauge group of gravity is not an idle one, for the attitude that we assume in this respect will determine the kind of questions that we are going to ask about the theory later." Role of Soldering Gravity Theory by Roberto Percacci

Interpretation

The most popular interpretation of general relativity is the geometric interpretation that is also found in most textbooks. It can be summarized as: There is no gravitational field. It is merely an illusion due to the curvature of spacetime.

A strong critic of the interpretation is S. Weinberg. In his famous book "Gravitation" he writes

However, I believe that the geometrical approach has driven a wedge between general relativity and the theory of elementary particles. As long as it could be hoped, as Einstein did hope, that matter would eventually be understood in geometrical terms, it made sense to give Riemannian geometry a primary role in describing the theory of gravitation. But now the passage of time has taught us not to expect that the strong, weak and electromagnetic interactions can be understood in geometrical terms, and too great and emphasis on geometry can only obscure the deep connections between gravitation and the rest of physics.

Another interpretation is the relational interpretation that is mainly advocated by C. Rovelli:

Einstein's major discovery is that spacetime and the gravitational field are the same object. A common reading of this discovery is that there is no gravitational field: just a dynamical spacetime. In view of quantum theory, it is more illuminating and more useful to say that there is no spacetime, just the gravitational field. From this point of view, the gravitational field is very much a field like any other field. Einstein's discovery is that the fictitious background spacetime introduced by Newton does not exist. Physical fields and the relations are the only components of reality.Quantum Gravity by Rovelli

Research

For a great overview see the chapter 7.6 Modifications and Extensions of/to General Relativity in the book Symmetries in Fundamental Physics by Sundermeyer.

Gauge Gravity

• Gauge Gravity: a forward-looking introduction by Randono
• Gauge Theories of Gravity - A reader with commentary by Hehl et. al.

Spacetime theories beyond General Relativity

There is no good reason why we should only focus on Riemannian manifolds like we do in general relativity. Manifolds can not only be curved but also have a nonzero torsion and nonzero non-metricity.

In general, a manifold is characterized by these three quantities:

Curvature

A manifold has a nonzero curvature if a vector that gets parallel transported along two differents loops is not the same.

Torsion

A manifold has nonzero torsion if the parallelogram that is formed by two vectors does not close.

Non-Metricity

A vector has nonzero nonmetricity if the length of vectors is not preserved.

Source: https://arxiv.org/pdf/1802.00492.pdf#page7

The standard formulation of general relativity only permits a non-zero curvature.

There is a lot of research on the question whether more general manifolds should also be studied, i.e. what happens when we relax the requirements of general relativity.

This is especially interesting in connection with the many open problems of general relativity, like the dark matter problem or the cosmological constant problem.

Einstein only considered mass points. However, nowadays we know that there are mass points with an internal structure, namely spin. An example of mass points with spin are fermions and an example of a fermion is an electron or a neutron.

“Newton successfully wrote apple = moon, but you cannot write apple = neutron”.https://arxiv.org/pdf/1204.3672.pdf

If we want to consider fermions in curved spacetime, we need to take torsion into account, i.e. consider manifolds with nonzero torsion.

All this can also be understood from a symmetry perspective.

Usually, we assume the local spacetime symmetry group is the Poincare group. Gravity couples to energy. The conservation of energy is a result of translational invariance. In this sense gravity can be understood as a gauge theory of translational symmetry.

If we gauge the full Poincare group, we also gauge rotations. The corresponding conserved quantity is angular momentum. If we do this, we get the result that gravity not only couples to energy, but also to angular momentum and we need to include torsion.

In addition, we can enlarge the spacetime symmetry group. The maximal symmetry group is the conformal group. This group contains in addition to translations and rotations also dilatations. (The Poincare group plus dilatations is known as Weyl group. The conformal group contains additional conformal transformation). Hence, if we gauge it we get the result that the gravitational field is not only given by curvature, torsion but also additionally non-metricity.

Alternative Descriptions of General Relativity

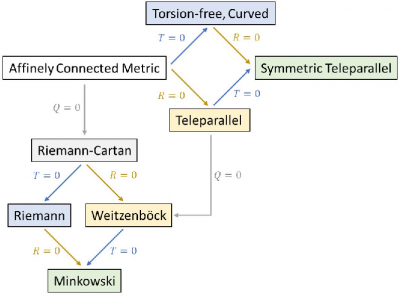
Instead of considering general relativity as a theory of Riemannian manifolds (only curvature zero), we can also consider other special cases like, for example, only non-zero torsion (and zero curvature and zero non-metricity) or only non-zero non-metricity (and zero curvature and zero torsio.)

Surprisingly, if we do this we end up with theories that are completely equal in terms of observational predictions to the standard formulation of general relativity.

The special case with only non-zero torsion is known as Weitzenböck gravity and the special case with only non-zero nonmetricity symmetric teleparallel gravity. (See the Venn diagram above).

Einstein’s celebrated theory of gravitation can be presented in three forms: general relativity, teleparallel gravity, and the rarely considered before symmetric teleparallel gravity. These for- mulations differ in the underlying geometric structure and interpretations, but are equivalent in observational predictions. The theories truly part when one extends them by e.g. nonminimally coupling a scalar field to the metric tensor degree of freedom. […]

It is a well known fact in differential geometry, that the most general affine connection can be decomposed into three parts,

\begin{equation} \label{Connection decomposition} \Gamma^{\lambda}_{\phantom{\alpha}\mu\nu} = \left\lbrace {}^{\lambda}_{\phantom{\alpha}\mu\nu} \right\rbrace + K^{\lambda}_{\phantom{\alpha}\mu\nu}+ L^{\lambda}_{\phantom{\alpha}\mu\nu} \,, \end{equation}

viz. the Levi-Civita connection of the metric $g_{\mu\nu}$,

\begin{equation} \label{LeviCivita} \left\lbrace {}^{\lambda}_{\phantom{\alpha}\mu\nu} \right\rbrace \equiv \frac{1}{2} g^{\lambda \beta} \left( \partial_{\mu} g_{\beta\nu} + \partial_{\nu} g_{\beta\mu} - \partial_{\beta} g_{\mu\nu} \right) \,, \end{equation}

contortion

\begin{equation} \label{Contortion} K^{\lambda}{}_{\mu\nu} \equiv \frac{1}{2} g^{\lambda \beta} \left( T_{\mu\beta\nu}+T_{\nu\beta\mu} +T_{\beta\mu\nu} \right) \, , \end{equation}

and disformation

\begin{equation} \label{Disformation} L^{\lambda}{}_{\mu\nu} \equiv \frac{1}{2} g^{\lambda \beta} \left( -Q_{\mu \beta\nu}-Q_{\nu \beta\mu}+Q_{\beta \mu \nu} \right) \,. \end{equation}

The last two quantities are defined via nonmetricity

\begin{equation} \label{NonMetricityTensor} Q_{\rho \mu \nu} \equiv \nabla_{\rho} g_{\mu\nu} = \partial_\rho g_{\mu\nu} - \Gamma^\beta{}_{\rho \mu} g_{\beta \nu} - \Gamma^\beta{}_{\rho \nu} g_{\mu \beta} \, \end{equation}

and torsion

\begin{equation} \label{TorsionTensor} T^{\lambda}{}_{\mu\nu}\equiv \Gamma^{\lambda}{}_{\mu\nu}-\Gamma^{\lambda}{}_{\nu\mu}\,. \end{equation}

By construction the contortion tensor is antisymmetric with respect to the first and third index $K^{\mu\lambda\nu}=-K^{\nu\lambda\mu}$, while the disformation tensor is symmetric with respect to the second and third index $L^{\lambda\mu\nu}=L^{\lambda\nu\mu}$.

One should note that nonmetricity, torsion, as well as curvature

\begin{equation} \label{Riemann_tensor} R^{\sigma}{}_{\rho\mu\nu} \equiv \partial_{\mu} \Gamma^{\sigma}{}_{\nu\rho} - \partial_{\nu} \Gamma^{\sigma}{}_{\mu\rho} + \Gamma^{\alpha}{}_{\nu\rho} \Gamma^{\sigma}{}_{\mu\alpha} - \Gamma^{\alpha}{}_{\mu\rho} \Gamma^{\sigma}{}_{\nu\alpha} \, \end{equation}

are strictly speaking all properties of the connection. By making assumptions about the connection we can define different geometries. Namely, in general metric-affine geometry nonmetricity, torsion and curvature are all in play. Taking only nonmetricity to vanish gives Riemann-Cartan geometry, taking only curvature to vanish gives teleparallel geometry (since the parallel transport of vectors becomes independent of the path), while taking torsion to vanish is just known as torsion free geometry. We can also impose double conditions on the connection. Demanding nonmetricity and torsion to vanish leaves us with Levi-Civita (LC) connection and Riemann geometry (in the narrow sense). Assuming nonmetricity and curvature to be zero is the premise of Weitzenböck (W) connection. Finally keeping torsion and curvature to zero means symmetric teleparallel (STP) connection and geometry. Finally, setting nonmetricity, torsion, and curvature all to zero, yields Minkowski space.

https://arxiv.org/pdf/1802.00492.pdf

Field Theories beyond General Relativity

Another possibility to modify general relativity is to add additional fields. Conventionall gravity is only mediated by the graviton field, which is represented by a spin $2$ tensor. It is possible to add additional fields like scalar (=spin 0) fields to the theory which then also mediate gravity. The most famous example is the Brans–Dicke theory of gravitation.

History

It is difficult to imagine how Einstein could have discovered general relativity, had he started by trying to fix the observed discrepancy in the precession of Mercury’s perihelion.3 Logical deduction, based on arguments like the equivalence principle, is what brought Einstein to his monumental theoretical construction. 3If one takes the discrepancy in Mercury’s data as starting point, the most straightforward solution would be postulating a new planet causing a perturbation in Mercury’s orbit. This is the approach followed by Urbain Le Verrier, who had been previously successful in predicting the existence of Neptune, and who tried his luck with a new planet he named Vulcan. The discovery of Vulcan was announced by Le Verrier in 1860, on the basis of observations made by an amateur astronomer, Edmond Modeste Lescarbault. The debate over the observations lasted for decades and, when he died in 1877, Le Verrier was still convinced about Vulcan’s existence [59].

https://arxiv.org/pdf/1710.07663.pdf#page23

Recommended Resources:

• http://www.mpiwg-berlin.mpg.de/Preprints/P264.PDF
• https://arxiv.org/abs/1201.5353