Intuitive

The Aharonov-Bohm experiment is basically a double-slit experiment with an added solenoid.

Image by Stevenj at the English language Wikipedia published under the CC-BY-SA-3.0 licence

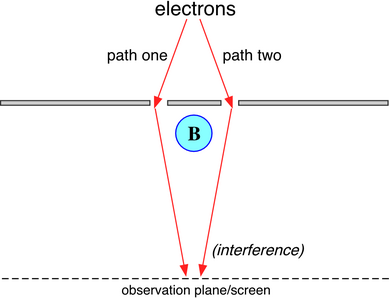
The magnetic field B is contained entirely inside the solenoid. In addition, the solenoid is shielded to keep the electrons out. Therefore, the electrons cannot “feel” B at all. Yet it makes a difference whether the B field is on or not.

The electrons “know” if a B field is there because, when they meet again at the screen, the interference pattern is different depending on whether there is a current flowing through the solenoid or not (i.e., when B = 0 ).

This can be understood by noting that while the B field on the outside is zero, the magnetic potential $A$ is not.

The effect of this magnetic potential is quite different from the effect of the B field. A B field pushes the electrons around. In contrast, the magnetic potential only changes the phase of the electrons. However, such a change of phase has an important effect, since it alters the interference pattern at the screen.

This way, the Aharonov-Bohm experiment shows that the magnetic potential is also important and not just a mathematical tool.

Source: https://edoc.ub.uni-muenchen.de/17735/1/Atala_Marcos.pdf

Concrete

The magnetic field is only nonzero in the interior of the solenoid. However, the associated vector potential can be nonvanishing also outside. Since the magnetic fields is zero outside, the value of $\vec{A}$ outside the solenoid has to be pure gauge, i.e. a gauge transformation of $\vec{A}=0$: $\vec{\nabla}\times\vec{A}=\vec{0}$.

This is important because the region outside the solenoid is not simply connected the vector potential cannot be gauged to zero everywhere, only patchwise.

We denote by $\Psi_{1}^{(0)}$ and $\Psi_{2}^{(0)}$ the wave functions for the two electron beams without the solenoid. The total wave function when we switch the magnetic field on is \begin{eqnarray} \Psi&=&e^{ie\int_{\Gamma_{1}}\vec{A}\cdot d\vec{x}}\Psi_{1}^{(0)}+ e^{ie\int_{\Gamma_{2}}\vec{A}\cdot d\vec{x}}\Psi_{2}^{(0)} \nonumber \\ &=&e^{ie\int_{\Gamma_{1}}\vec{A}\cdot d\vec{x}}\left[\Psi_{1}^{(0)} +e^{ie\oint_{\Gamma}\vec{A}\cdot d\vec{x}}\Psi_{2}^{(0)}\right] \label{eq:extra_phase} . \end{eqnarray} Here $\Gamma_{1}$ and $\Gamma_{2}$ denote two curves surrounding the solenoid from different sides. In addition, $\Gamma$ is any closed loop surrounding it.

We can see here that the relative phase between the two beams going different paths, gets an additional contribution that depends on the value of the vector potential \begin{eqnarray} U=\exp\left[ie\oint_{\Gamma}\vec{A}\cdot d\vec{x}\right]. \label{eq:wilson} \end{eqnarray}

This way the presence of the magnetic field becomes visible through a changed interference pattern even though it is zero outside of the solenoid.

Take note that the quantity $U$ is independent of the gauge we are working in. Moreover, take note that the value of $U$ does not change when we continuously deform our curve $\Gamma$ around the solenoid, as long as both path stay on opposite sides of the solenoid.

• The best explanation can be found here: http://gregnaber.com/wp-content/uploads/GAUGE-FIELDS-AND-GEOMETRY-A-PICTURE-BOOK.pdf at page 18ff
• See also https://www.dartmouth.edu/~dbr/topdefects.pdf

For quite some time it was felt that such phase changes in the wavefunction were of no physical significance since all of the physically measurable quantities associated with the charge q depend only on the squared modulus $|ψ|^2$ and this is the same for $ψ$ and $e^{iqΩ} ψ$. However, in 1959, Aharonov and Bohm [AB] suggested that, while the phase of a single charge may well be unmeasurable, the relative phase of two charged particles that interact should have observable consequences. They proposed an experiment that went roughly as follows: A beam of electrons is split into two partial beams that pass around opposite sides of a solenoid (this is a very tightly wound coil of wire through which a current passes, creating a magnetic field that is confined inside the coil ). Beyond the solenoid the beams are recombined and detected at a screen. The result is a typical interference pattern that manifests itself experimentally as a variation from point to point on the screen of the prob- ability of detecting a particle there. One observes this interference pattern when there is no current flowing through the coil, so that the magnetic field in the solenoid is zero, and then again when there is a current and hence a nonzero magnetic field inside the coil. Since the electrons pass around the coil and the magnetic field is confined inside the coil, any shift in the interference pattern in these two cases cannot be attributed to the magnetic field (which the electrons do not encounter). The vector potential, on the other hand, is generally nonzero outside the solenoid even though the magnetic field in this region is always zero. One could then only conclude that this vector potential induces different phase shifts on the two partial beams before they are recombined and that these relative phase changes account for the altered interference pattern. This experiment has, in fact, been performed (first by R. G. Chambers in 1960) with results that confirmed the expectations of Aharonov and Bohm.page 6 in Topology, Geometry and Gauge Fields: Foundations by Naber

Abstract

The Aharonov-Bohm experiment can be understood nicely using fiber bundles. A different path through around the solenoid leads to a different path through the fiber bundle and thus to a netto phase difference

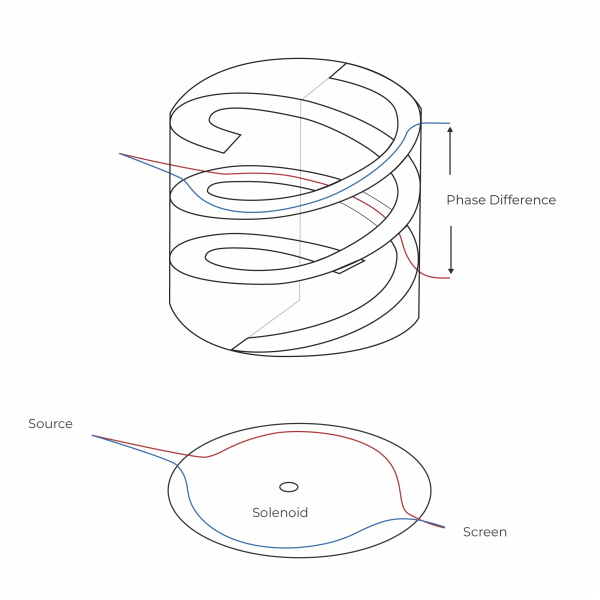The gauge field $A$ is responsible that electrons moving on opposite sides around the solenoid also need to take different paths around the fiber bundle. In the picture above, the gauge field corresponds to the ramps that tell us how the phase factor of an electron changes as it moves through space.

Topologically, the solenoid is a defect. There are no fields outside the solenoid so the energy density of the fields are zero and there is a true vacuum, however, the vector potential changes the topology of the vacuum. We are familiar with the gauge idea that the vector potential can be written as the gradient of some other function χ so that ∇ × ∇χ = 0 identically. We can calculate χ by integrating the vector potential outside the solenoid with respect to the azimuthal coordinate Aθ = 1 r ∂χ ∂θ = BR2 2r or χ = 1 2BR2 θ which we see is not a single valued function of θ, that is χ(θ) 6= χ(θ + 2π). Functions that are not single valued can only exist in spaces that are not simply connected, or those that do not have trivial first homotopy group. We see that the manifold of the vacuum is thus the key to understanding the new physical result, and the topological defect gives us the intuition

http://www.dartmouth.edu/~dbr/topdefects.pdf

• For the topology behind the Aharonov-Bohm effect, see section 10.5.3. in Geometry, Topology and Physics by Nakahara.

Why is it interesting?

The Aharonov-Bohm experiment demonstrated that that the gauge potential is not just a convenient mathematical notion, but physically real.