Intuitive

A phase space is a mathematical tool that allows to grasp important aspects of complicated systems.

Each point of the phase space represents one specific configuration a given system can be in.

The state of a system is recorded in a phase space point through all the location and all the momenta the objects in the system have at a given point in time.

The time evolution of a system can then be represented as a path in phase space.

Concrete

Each point of the phase space corresponds to one particular state of the system.

The form of the Hamiltonian equations allows us to 'visualize' the evolution of a classical system in a very powerful and general way. Try to imagine a 'space' of a large number of dimensions, one dimension for each of the coordinates $x_1, x_2,\ldots$, $p_1, p_2,\ldots$ (Mathematical spaces often have many; more than three dimensions.) This space is called phase space (see Fig. 5.10). For n unconstrained particles, this be a space of 6n dimensions (three, position coordinates and three momentum coordinates for each particle). The reader may well worry that even for a single particle this is already twice as many dimensions as she or he would normally be used to visualizing! The secret is not to be put off by this. Whereas six dimensions are, indeed, more dimensions than can be readily pictured, it would actually not be of much to us if we were in fact able to picture it. For just a room full of molecules, the number of phase-space dimensions might be something like

$$ 100000000000000000000000000 . $$

There is no much hope in trying to obtain an accurate visualization of a space that big! Thus, the trick is not even to try - even in the case of the phase space of a single particle. Just think of some vague kind of three-dimensional (or even just two-dimensional) region. Have another look at Fig. 5. 10. That will do.

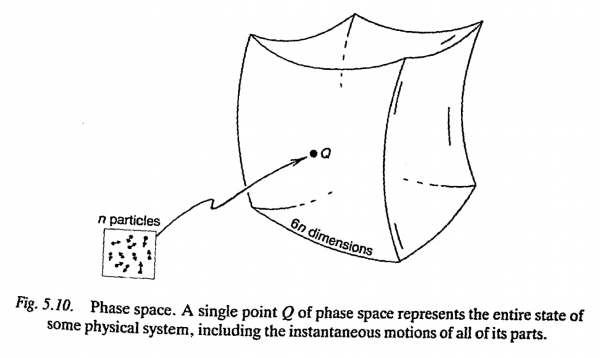
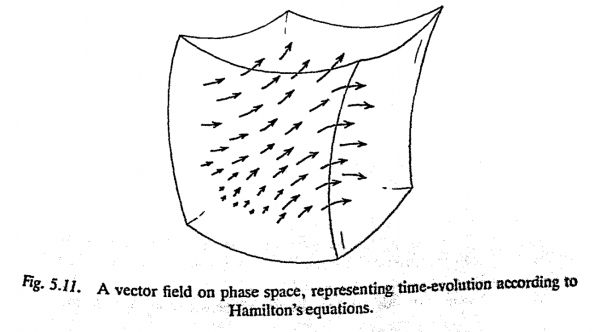
Now, how are we to visualize Hamilton's equations in terms of phase Space? First, we should bear in mind what a single point Q of phase space actually represents. It corresponds to a particular set of values for all the position coordinates $x_1,x_2,\ldots.$ and for all the momentum coordinates $p_1,p_2, … $ That is to say, Q represents our entire physical system, with a particular state of motion specified for every single one of its constituent particles. HamIlton's equations tell us what the rates of cbange of all these coordinates are,.wben we know their present values; i.e. it governs how all the individual particles are to move. Translated into phase-space language, the equations are tellingus how a single point Q in phase space must move, given the present location of Q in phase space. Thus, at each point of phase space, we have a little arrow - more correctly a vector- which tells us the way that Q is moving, in order to describe the evolution of our entire system in time. The whole arrangement of arrows constitutes what is known as a vector field (Fig. .11). Hamilton's equations thus define a vector field on phase space.

Let us see how physical determinism is to be interpreted in tel filS of phase space. For initial data at time t = 0, we would have a particular set of values ~specified for all the position and momentum coordinates; that is to say, we have a particular choice of point Q in phase space. To find the evolution of the system in time. we simply follow the arrows. Thus the entire evolution of our system with time - no matter how complicated that system might be - is described in phase space as just a single point moving along following the particular arrows that it encounters. We can think of the arrows as indicating the "velocity" of our point Q in phase space. For a "long" arrow, Q moves along swiftly, but if the arrow is "short", Q's motion will be sluggish. To see what our physical system is doing at time t, we simply look to see where Q has moved to, by that time, by following arrows in this way. Clearly this is a deterministic procedure. The way that Q moves is completely determined by, the Hamiltonian vector field.

page 174ff in "The Emperors new Mind" by R. Penrose

Abstract

The space of states in classical mechanics is modeled as a manifold $M$ equipped with a symplectic structure: $(M,ω)$. This manifold is what we usually call phase space. The phase space is a symplectic manifold which simply means that is a manifold equipped with a symplectic structure. A symplectic structure is a distinguished 2-form $(\omega)$.

Such a 2-form is an object that eats two vector fields on our manifold and returns another function on the manifold. Functions on the manifold are smooth maps $f \ : \ M \longarrow R$. These functions are what we call “the observables of our classical system”. So in words, this means that the observables of our classical system map each state to a real number.

One of the most important function on our phase space manifold is the Hamiltonian function. This function represents the energy of the system and describes the time-evolution of phase space points.

Why is it interesting?

Hamiltonian Mechanics is geometry in phase space. […]

Mathematical Methods of Classical Mechanics Vladimir Arnold

While it is true that the primary perception we, human beings, have of our world privileges positions, and their evolution with time, this does not mean that we have to use only, mathematics in configuration space. As Basil Hiley puts it “…since thoughts are not located in space-time, mathematics is not necessarily about material things in space- time”. Hiley is right: it is precisely the liberating power — I am tempted to say the grace — of mathematics that allows us to break the chains that tie us to one particular view of our environment." The Principles of Newtonian and Quantum Mechanics: by Gosson

History

See: The tangled tale of phase space by David D. Nolte https://works.bepress.com/ddnolte/2/download/