Add a new page:
Manifolds are especially important in General Relativity. Through massive objects, spacetime is curved and no longer flat. Manifolds are the correct mathematical tool to describe spacetime when it isn't flat.
The standard sentence is: A Manifold is a set of points that locally "looks the same" as some Euclidean space. Such geometric spaces are particularly nice to investigate, because we can use, locally, the familiar tools from elementary calculus. Happily, such spaces are not only nice to investigate, but also useful in physics to describe nature.
The idea of locality is made precise by the mathematical concept of a neighborhood. To each point of the manifold, a neighborhood must exist that is just like a small piece of Euclidean space.
Illustration of the map from some two-dimensional manifold $M$ onto $R^2$. The neighborhood $U$ of $P$ in $M$ is mapped onto $V$ in $R^2$. This map provides a coordinate system in the neighborhood of $P$. The idea of "looks like Euclidean space" is made precise by the concept of a diffeomorphism. If there exists a map: smooth, one-to-one, onto, and with a smooth inverse, (=a diffeomorphism) for each neighborhood onto some piece of Euclidean space, the space in question is a manifold.
This map from some neighborhood $X$ of the manifold onto Euclidean space gives us local coordinates of the points in this neighborhood. The inverse map is called a parametrization of the neighborhood. Therefore another way of thinking about an n-dimensional manifold is that its a set which can be given n independent coordinates ins some neighborhood of any point.
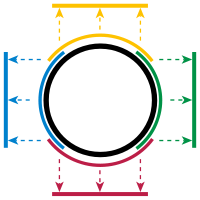
An example for a manifold is the unit circle $S^1$, mathematically defined as the set of points fulfilling the condition $x^2+y^2=1$. This is commomly expressed as:
\begin{equation} S^1 = \{ (x,y) \in R^2 : x^2+y^2 =1 \} \end{equation}
This manifold is one dimensional, hence the $1$ behind the $S$, because two degrees of freedom $x,y$ are reduced to one by the condition $x^2+y^2=1$. To see that this is a manifold, we need to find a map to each neighborhood onto Euclidean space.
The upper semicircle ($y>0$) is parametrized by $\Phi_1(x)=(x,\sqrt{1-x^2})$. $\Phi_1(x)$ maps the open interval $-1<x<1$ bijectively onto the upper semicircle. The inverse map is smooth and gives us coordinates of the upper semicircle.
For the lower semicircle ($y<0$) a parametrization is $\Phi_2(x)= (x,-\sqrt{1-x^2})$. Therefore we have found so far two local parametrizations.
These maps do not cover the points $(1,0)$ and $(-1,0)$ and we need further maps for the neighborhoods of these points: $\Phi_3(y)= (\sqrt{1-y^2},y)$ and $\Phi_4(y)= (-\sqrt{1-y^2},y)$. These maps are appropriate for the right- and left-half the circle. Nevertheless they not include $(0,1)$ and $(0,-1)$.
We can see that the neighborhoods overlap, which is no problem.
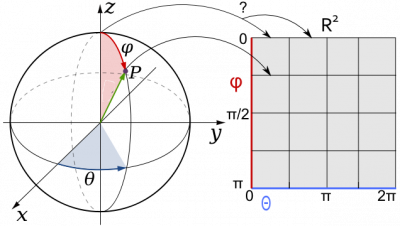
Another example of a manifold is the two-sphere. The two-sphere $S^2$ is defined as the set of points in $R^3$ for which $x^2+y^2+z^2=const$ holds, where $const$ is, of course, the radius of the sphere. The two-sphere is two-dimensional because the definition involves $3$ coordinates and one condition, which eliminates one degree of freedom. Therefore to see that the sphere is a manifold we need a map onto $R^2$. This map is given by the usual spherical coordinates. Almost all points on the surface of the sphere can be identified unambiguously with a coordinate combination of the form $(\varphi, \theta)$. Almost all! Where is the pole $\varphi=0$ mapped to? There is no one-to-one identification possible because the pole is mapped to a whole line, as indicated in the image.Therefore this map does not work for the complete sphere and we need another map in the neighborhood of the pole to describe things there. A similar problem appears for the map on the semicircle $\theta=0$. Each point can be mapped to in the $R^2$ to $\theta=0$ and $\theta=2 \pi$, which is again not a one-to-one map. This illustrates the fact that for manifolds there is in general not one coordinate system for all points of the manifold, only local coordinates, which are valid in some neighborhood. This is no problem because a manifold is defined to look locally like $R^n$.
The spherical coordinate map is only valid in the open neighborhood $0< \varphi <\pi , 0< \theta < 2 \pi$ and we need a second map to cover the whole sphere. We can use for example a second spherical coordinate system with a different orientation, such that the problematic poles lie at different points for this map and no longer at $\varphi=0$. With this second map, every point of the sphere has a map onto $R^2$ and the two-sphere can be seen to be a manifold.
Another trivial example for a manifold is of course $R^n$.