Intuitive

Phase factors $e^{i \phi(\vec x,t)}$, like they appear in quantum mechanics, are just complex numbers with amplitude $1$. Therefore, we can picture them as points on a circle with radius $1$:

This collection of all complex numbers with amplitude $1$ is what we call the group $U(1)$.

Concrete

Lie Algebra

The Lie algebra corresponding to the group U(1) is usually identified with the set of pure imaginary numbers $Im \mathbb{C} = \{ i \theta : \theta \in \mathbb{R} \}$.

Take note that the tangent space of a circle is, of course, just a copy of $\mathbb{R}$ but the isomorphic space $Im \mathbb{C}$ is more convenient because its elements can be "exponentiated" to give the elements $e^{i \theta}$ of $U(1)$.

Representations

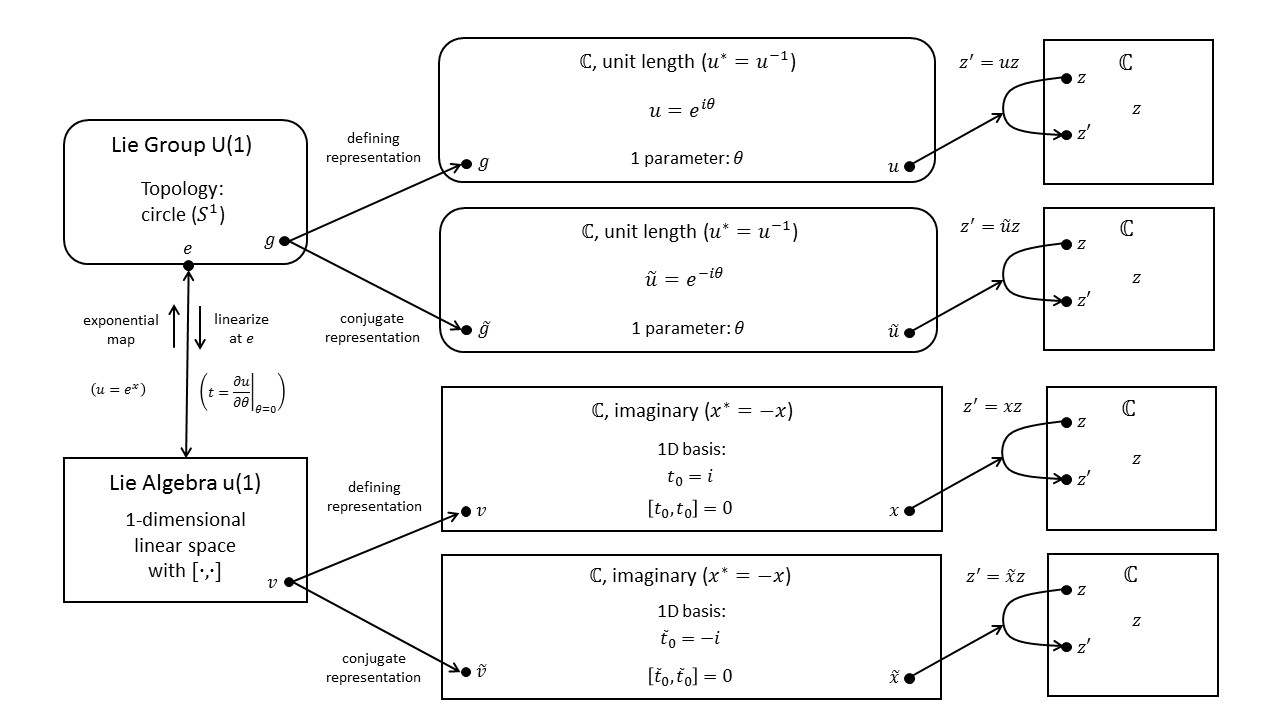
The diagram below shows the defining representation of $U(1)$ in its upper branch and the conjugate representations of the same group in its lower branch. For a more detailed explanation of this diagram and more representations of $U(1)$ see Fun with Symmetry.

Abstract

Why is it interesting?