Add a new page:
Sidebar
advanced_tools:connections:levi_civita_connection
$ \Gamma_{ijk} \equiv -\bigl(\partial_{i}g_{jk}-\partial_{k}g_{ij}-\partial_{j}g_{ki}\bigr)$
Levi-Civita Connection
also known as Christoffel Symbols; see also Connections
Intuitive
The Levi-Civita connection is a mathematical tool that we use to parallel transport vectors around a manifold.
Parallel transport is just the simplest way to compare vectors at different points in the manifold.
Parallel is necessary, for example, to define the covariant derivative.
Concrete
Christoffel symbols $\Gamma^i_{jk}$ are a particular type of connection that a Lorentzian manifold has (called the Levi-Civita connection).
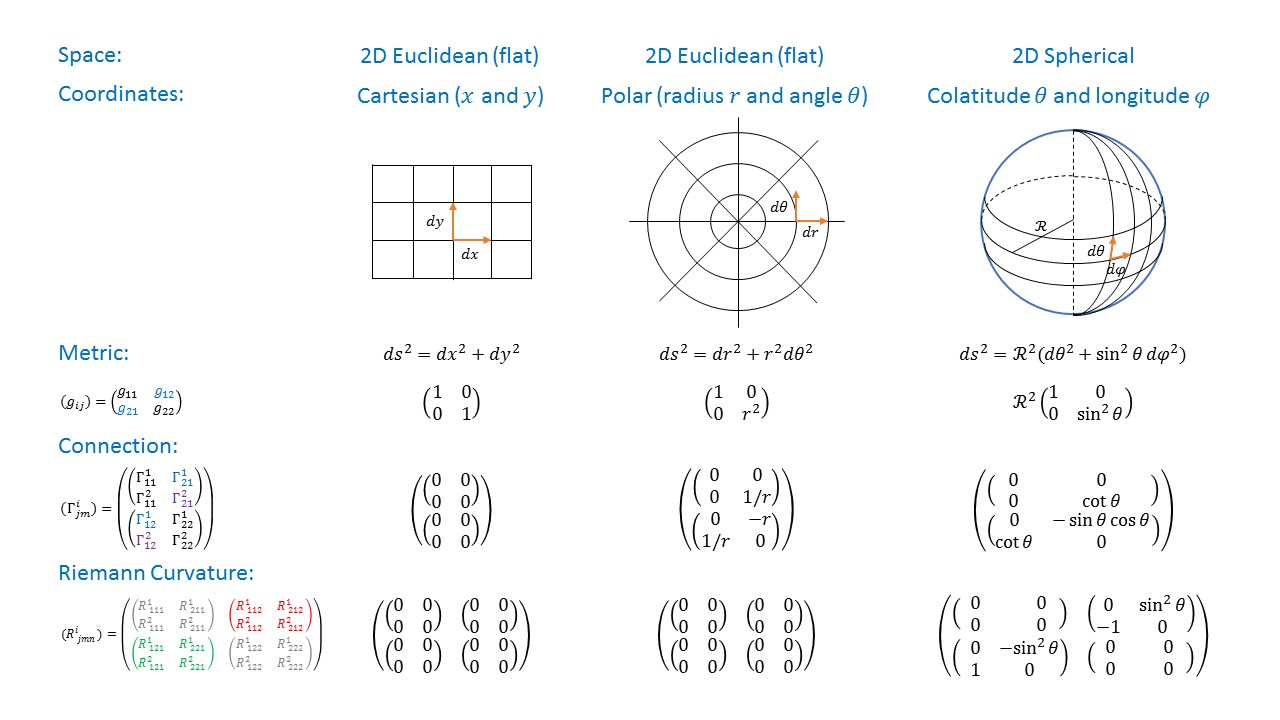
Examples
The diagram below shows three concrete examples for connections (Christoffel symbols) on simple 2-dimensional manifolds. For a more detailed explanation see Fun with Symmetry.
Abstract
The motto in this section is: the higher the level of abstraction, the better.
Why is it interesting?
The Christoffel symbols appear in the most important equations of general relativity: the Einstein equation and the geodesic equation.
advanced_tools/connections/levi_civita_connection.txt · Last modified: 2023/04/02 03:28 by edi
Except where otherwise noted, content on this wiki is licensed under the following license: CC Attribution-Share Alike 4.0 International
