Add a new page:
see also connections
To understand parallel transport imagine you're holding a long stick in your hand. You are then asked to walk a given path while keeping the stick straight all the time. What you are doing then is a parallel transport of the stick.
The important thing is now that if you do this and walk a closed curve, i.e. you end up where you started, the final position of the stick will not be the same as the initial position. This happens no matter how good you are in keeping the stick straight.
For example, consider two different paths around a ball as shown in the image below.
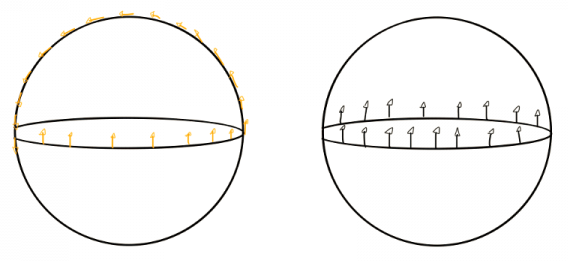
If you follow the path on the left-hand side, where the position of the stick corresponds to the yellow arrows, the final position of the stick is not the initial position, since a ball is curved and not flat.
Parallel transport on a sphere can best be understood by imagining the sphere to be rolling on a flat surface. Suppose there are straight lines and curved lines drawn on the flat surface in wet ink. And suppose there are arrows spaced frequently along the line, all pointing, say, to the lower left. The term "parallel transport" is based on this picture. Since the arrows in the plane are all parallel, the arrows printed onto the sphere exemplify parallel transport along the printed curve on the sphere.
Given a curve on the sphere and an arrow representing a direction at the start of the ruve, one can place the sphere on the plane so that the starting point is the point of tangency. Imagine there is an arrow at each point in the plane drawn in ink and parallel to the original arrow. If the sphere is rolled along the plane so that it prints the curve on the sphere onto the plane, the arrows from the plane will also be printed onto the sphere. The latter arrows give a path in the bundle of directions that starts with the initial arrow and lies above the given curve.
When a straight line is printed onto the rolling sphere (or onto any other curved surface), the curve that it forms on the surface is called a geodesic.
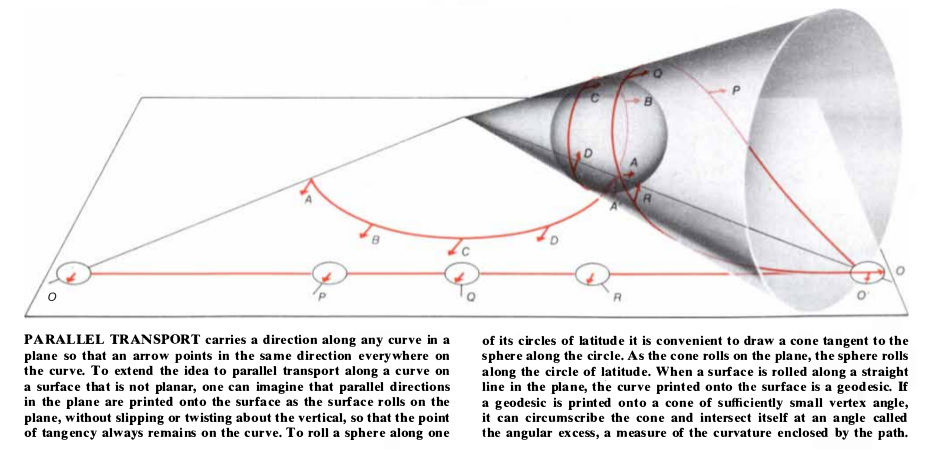
Parallel transport can be described for a curved path made up of geodesic segments without reference to rolling. It can be carried out by maintaining a constant angle between the transported arrows and the tangents along successive geodesics. From a perspective above the surface of the sphere, however, parallel transport along a geodesic may seem anything but parallel. The arrows may appear to rotate. When an arbitrary curved line is printed onto the sphere, the rotation of the arrows as viewed from above the surface may appear to be even more chaotic.
Parallel transport provides a way of making quantitative and explicit the intuitive difference between a curved surface and a flat one. When an arrow is carried by parallel transport around a closed path in the plane, the directions of the arrow at the start and at the finish coincide. Parallel transport around a closed path on a curved surface, however, may not lead to such coincidence. If there is a change in the direction of the arrow when it completes a single circuit of a closed path, the angle between the final direction and the initial one is called the angular excess of the path. It follows from the way parallel transport is defined that the angular excess does not depend on the initial direction of the arrow.
Fiber Bundles and Quantum Theory by Bernstein and Phillips
Mathematically, to parallel transport a given vector we need a connection.
The idea of parallel transport is important when we want to find out whether a given space is curved or not.