Intuitive

The Lie group $SO(3)$ describes all possible rotations of an object in 3-dimensional Euclidean space. It thus describes an important symmetry of the physical space we live in. (Other important spacetime symmetries are translations and boosts.)

$SO(3)$ is closely related to the groups $SU(2)$ and $Sp(1)$. They are all locally isomorphic, that is, they have the same Lie algebra.

Concrete

A general element of $SO(3)$ can be written as the product of three rotation matrices, one about the $x$, $y$, and $z$ axes: $R(\theta_x,\theta_y,\theta_z) = R_x(\theta_x) \cdot R_y(\theta_y) \cdot R_z(\theta_z)$, where

\begin{eqnarray} & & R_x(\theta_x) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\theta_x & -\sin\theta_x \\ 0 & \sin\theta_x & \cos\theta_x \end{pmatrix}, \label{eq:rotx} \\ & & R_y(\theta_y) = \begin{pmatrix} \cos \theta_y & 0 & \sin\theta_y \\ 0 & 1 & 0 \\ -\sin\theta_y & 0 & \cos\theta_y \end{pmatrix}, \label{eq:roty} \\ & & R_z(\theta) = \begin{pmatrix} \cos \theta_z & -\sin \theta_z & 0 \\\sin\theta_z & \cos\theta_z & 0 \\ 0 & 0 & 1 \end{pmatrix}. \label{eq:rotz} \end{eqnarray}

Representations

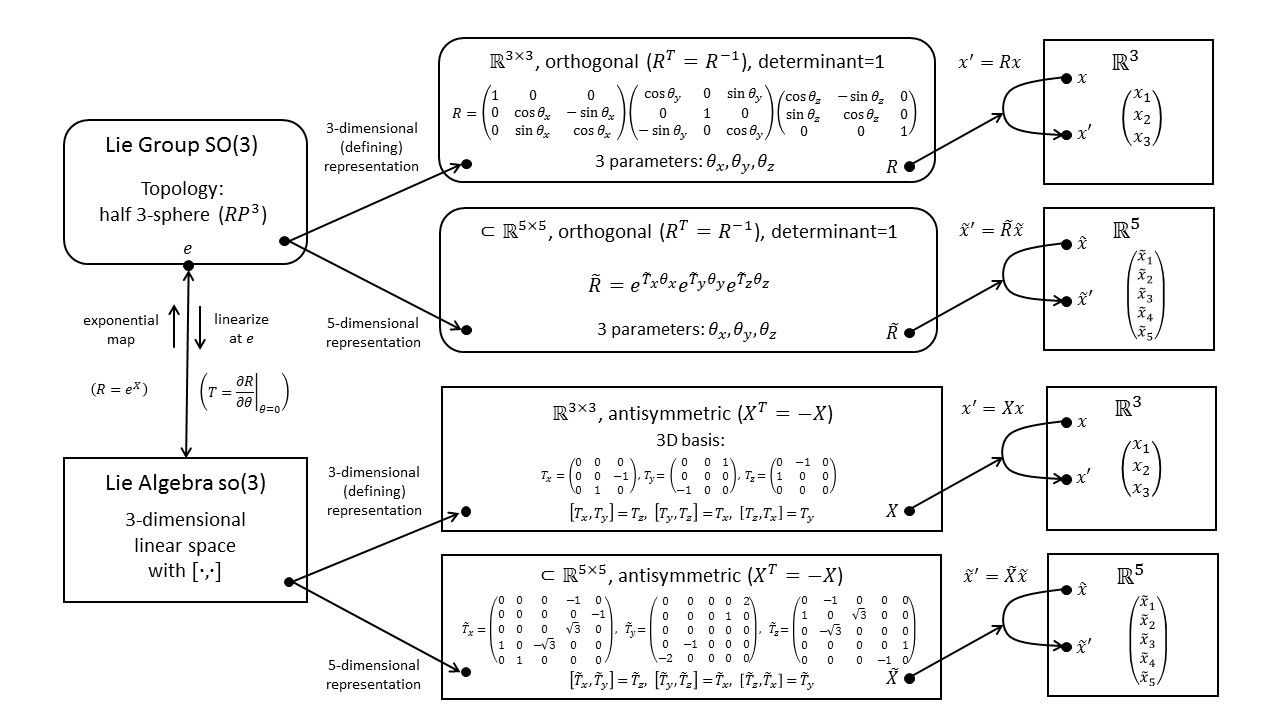
The diagram below shows the defining (3-dimensional) representation of $SO(3)$ in its upper branch and a 5-dimensional representation of the same group in its lower branch. For a more detailed explanation of this diagram, see Fun with Symmetry.

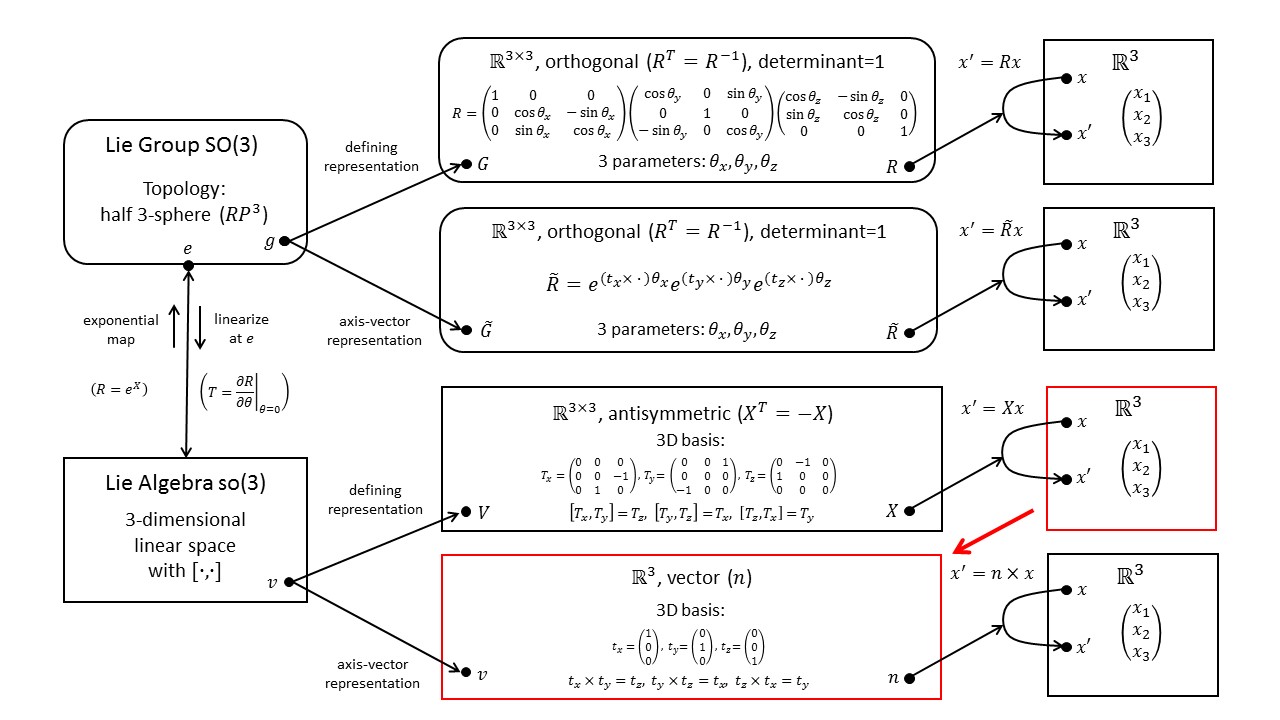
Instead of using 3x3 matrices for the Lie-algebra elements of the defining representation, we can also use 3-dimensional vectors (red box in the diagram below). Then, the Lie-algebra elements act on the representation space by means of the cross product (lower branch of the diagram). For a more detailed explanation of this diagram, see Fun with Symmetry.

Abstract

Why is it interesting?