Intuitive

Given an $n$- and $m$-dimensional representations, we can construct an $nm$-dimensional tensor-product representation by letting it act on the tensor-product space. In particular, we can construct an $n^2$-dimensional representation from two copies of an $n$-dimensional representation.

Tensor-product representations are useful for constructing new representations from old ones. Take the product of two old representations and break the result up into irreducible representations.

In quantum mechanics, tensor-product representations are useful for describing multi-particle systems and study entanglement among the particles.

Concrete

Example

The diagram below shows the defining representation of $SU(2)$ in its upper branch. To construct the tensor-product representation from two copies of the defining representation, we let it act on the tensor-product space, $\mathbb{C}^2 \otimes \mathbb{C}^2$, as shown in the lower branch.

The resulting 4-dimensional representation is reducible, breaking up into a 1- and 3-dimensional irreducible representation. This is usually written as $\bf 2 \otimes 2 = 1 \oplus 3$.

This tensor-product representation is useful for describing a system of two spin-1/2 particles, in particular, to analyze the spin states of the combined system.

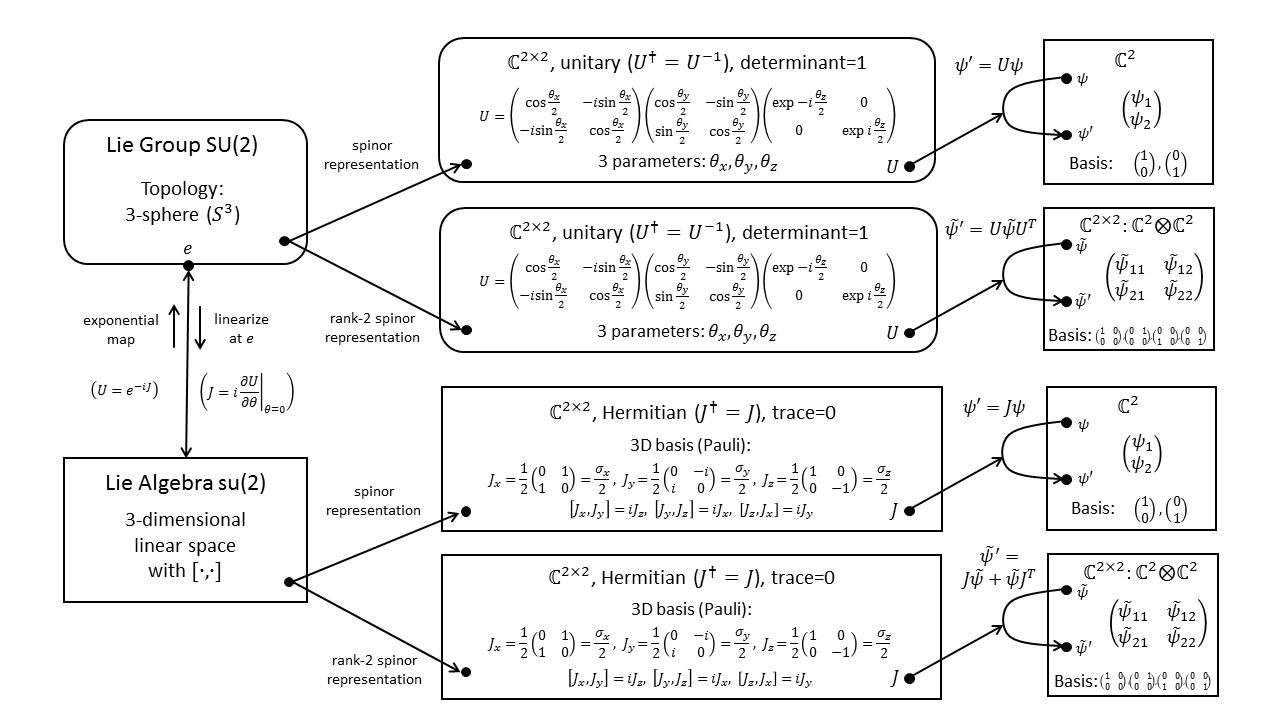
For a more detailed explanation of this diagram see Fun with Symmetry.

Abstract

Why is it interesting?