Intuitive

The trivial representation maps all group elements to the identity element. This representation exists for any group.

Spin-$0$ particles transform under the trivial representation of $SU(2)$. That is, their spin value does not change under rotation.

The action (and often the Lagrangian) transforms under the trivial representation of the Lorentz group and the relevant gauge groups. That is, the action is not affected by these symmetry transformations.

Concrete

Example

The diagram below shows the defining representation of $SU(2)$ in its upper branch and the trivial (1-dimensional) representation in its lower branch.

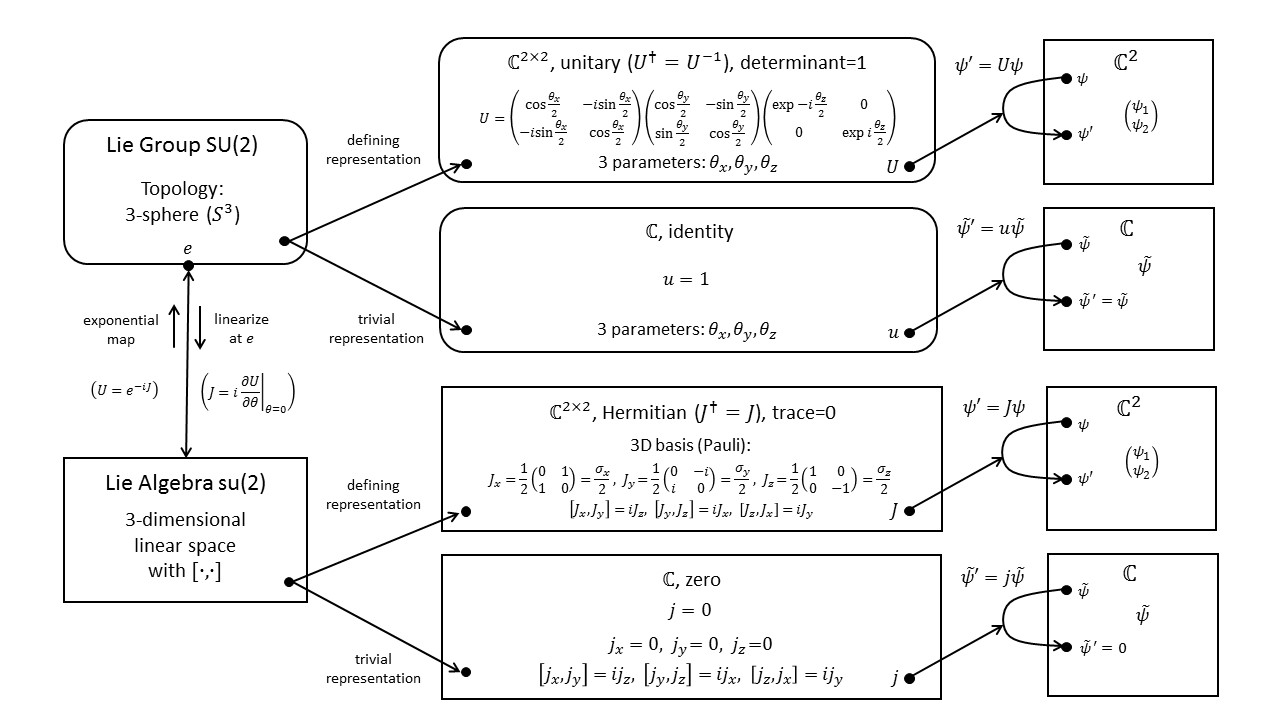
For a more detailed explanation of this diagram see Fun with Symmetry.

Abstract

Why is it interesting?