Intuitive

The exterior derivative generalizes the curl operator from 3-dimensional space to any number of dimensions.

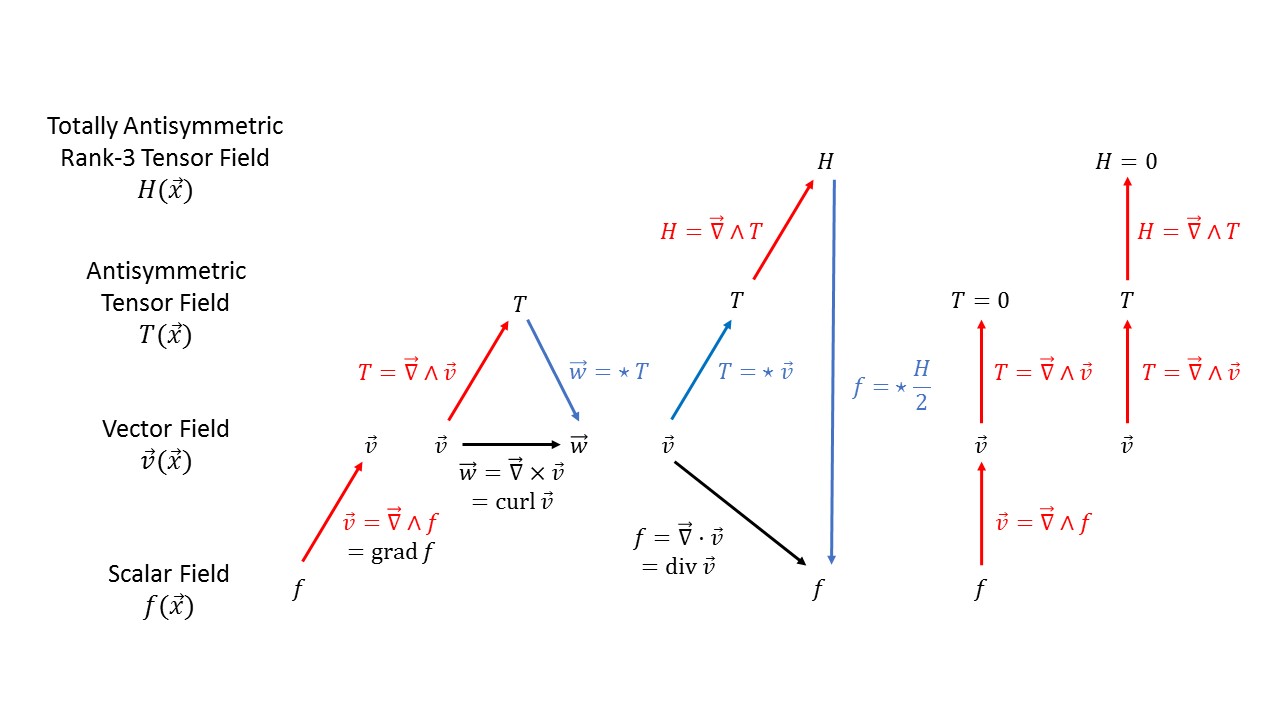
The exterior derivative of a vector field $v$ can be written as $\nabla \wedge v$, where the $\wedge$ indicates the exterior product. This is analogous to how we can write the curl as $\nabla \times v$, where $\times$ is the cross product, and the divergence as $\nabla \cdot v$, where $\cdot$ is the dot product. The result of $\nabla \wedge v$ is an anti-symmetric tensor field.

In 3-dimensional space, the curl operator is equal to the Hodge dual of the exterior derivative: ${\rm curl}(v) = \star(\nabla \wedge v)$.

The exterior derivative of a $p$-form $\omega$ is commonly written as $d\omega$. The result of $d\omega$ is a ($p+1$)-form.

Taking the exterior derivative twice (of any object) results in zero: $d^2\omega=0$. This is an important result with many implications for electrodynamics, topology, etc.

Concrete

The diagram shows on the left-hand side how the gradient, curl, and divergence operators know from 3D can be constructed from the exterior derivative and the Hodge dual. The right-hand side illustrates the fact that taking the exterior derivative twice results in zero.

For a more detailed explanation of this picture see Fun with Symmetry.

Abstract

Why is it interesting?