Grand Unified Models

Intuitive

The similarities between the vacuum of space and low-temperature phases of matter are legendary in physics. Not only are phases static,uniform quantum states, but their most subtle internal motions are physically indistinguishable om elementary particles very generally.3This is one of the most astonishing facts in science, and something students always find upsetting and difficult to believe. But they even­tually become convinced a er looking at enough experiments, for the evidence is plenti l and consistent. In fact, the more one studies the mathematical descriptions of cold phases, the more accustomed one gets to using the parallel terminologies of matter and space inter­changeably. Thus instead of a phase of matter we speak of a vacuum.Instead of particles we speak of excitations. Instead of collective mo­tions we speak of quasiparticles. The pre x "quasi" turns out to be a vestige of the historical battles over the physical meaning of these ob­jects and conveys no meaning. In private conversations one drops the pretense and refers to the objects as particle

[…]

The vacuum, when cooled from very high temperatures, is thought to undergo stepwise events called unification transitions, in which the known forces of nature split off sequentially from their fundamental parent. Similarly, holmium metal, a rare earth element, when cooled from very high temperature, first condenses into a liquid at 2993 degrees Kelvin, then solidifies at 1743 degrees, then develops a special kind of spiraling magnetism at 130 degrees, then tils the spiral to make weak ferromagnet at 20 degrees. Between 130 degrees and 20 degrees the pitch of the spiral varies continuously, as though it were a rubber screw being stretched along its axis. With each of these transitions the "forces" between electrons in the metal transmitted by various elastic distortions of the ordered state split off from the fundamental parent in beautiful and apt analogy with what occurs in the vacuum. The temperatures required to see the unification transitions of the vacuum cannot be achieved in the laboratory, or even in the centers of the largest stars, so the evidence for unification is indirect, but it nicely parallels what one would find in the tilted spiral magnet if one's experiments could reach only long length and time scales. One of the strongest of these bits of evidence is renormalizability, an effect that causes the accessible measurements to be simple and redundant (one measurement predicts another) but that at the same time is incapable of revealing anything about the forces at the top of the hierarchical tree.

[…]

There are numer­ous experimental indications that the vacuum emerges in a hierarchy of phase transitions in which the various forceS differentiate from each other….

If renormalizability of he vacuum is caused by proximity to phase transitions th the search for an ultimate theory would been doomend on two counts: it would not predict anything even if you found it, and it could not be falsified.

page 112 in "A different Universe" by Robert Laughlin

Concrete

Abstract

Why is it interesting?

Despite the success of the standard model, there are several reasons to believe that it is not the final description of nature at the most fundamental level. For example, there is no explanation in the standard model why $Q_{\text{proton}}+Q_{\text{electron}}= \mathcal{O}(10^{-20})$. The success of the standard model, tells us that nature likes gauge theories. Thus in order to find answers to questions left unanswered by the standard model, we follow the gauge idea further. The basic hypothesis of grand unified theories (GUTs) is that we embed the standard model gauge group in a simple group $G_{GUT} \supset G_{SM}$. This way the strong and electroweak interactions are unified and we are left with a single gauge coupling constant. In present day colliders, we do not observe effects of a $G_{GUT}$ structure and thus we assume the unified gauge symmetry is broken at some high energy scale \begin{equation} \label{eq:schematicgutbreaking} G_{GUT} \stackrel{M_{GUT}}{\rightarrow} \ldots \stackrel{M_I}{\rightarrow} G_{SM} \stackrel{M_Z}{\rightarrow} SU(3)_C \times U(1)_Q \, , \end{equation} where the dots indicate possible intermediate scales between $G_{GUT}$ and $G_{SM}$. Here are some of the "mysteries" of the standard model that can be resolved by a GUT:

Quantization of Electric Charge
In the standard model the electric charges of the various particles must be put in by hand and there is no reason why there should be any relation between the electron and proton charge. However from experiments it is known that $Q_{\text{proton}}+Q_{\text{electron}}= \mathcal{O}(10^{-20})$. In GUTs one multiplet of $G_{GUT}$ contains quarks and leptons. This way, GUTs provide an elegant explanation for the experimental fact of charge quantization.

\begin{equation} \bar{5} = \begin{pmatrix} \nu_L \\ e_L \\ (d_R^c)_{\text{red}} \\ (d_R^c)_{\text{blue}} \, .\\ (d_R^c)_{\text{green}} \end{pmatrix} \end{equation}

The standard model generators must correspond to generators of $G_{GUT}$. Thus the electric charge generator must correspond to one Cartan generator\footnote{The eigenvalues of the Cartan generators of a given gauge group correspond to the quantum numbers commonly used in particle physics. This is discussed in section \ref{sec:easysu3intro}.} of $G_{GUT}$. In $SU(5)$ the Cartan generators can be written as diagonal $5\times 5$ matrices with trace zero\footnote{In $SU(5)$ is the set of $5 \times 5$ matrices $U$ with determinant $1$ that fulfil $U^\dagger U = 1$. For the generators $T_a$ this means $\text{det}(e^{i \alpha_a T_a})=e^{i \alpha_a \text{Tr}(T_a)} \stackrel{!}{=}1$. Therefore $Tr(T_a) \stackrel{!}{=} 0$}. Therefore we have

\begin{align} \text{Tr}(Q)&= \text{Tr} \begin{pmatrix} Q(\nu_L) & 0 & 0 & 0 &0 \\ 0 & Q(e_L) & 0 & 0 &0 \\ 0 & 0 & Q((d_R^c)_{\text{red}}) & 0 &0\\ 0 & 0 & 0 & Q((d_R^c)_{\text{blue}})&0\\ 0 & 0 & 0 & 0 &Q((d_R^c)_{\text{green}}) \end{pmatrix} \stackrel{!}{=} 0 \notag \\ &\rightarrow Q(\nu_L) + Q(e_L) + 3Q(d_R^c) \stackrel{!}{=} 0 \notag \\ &\rightarrow Q(d_R^c) \stackrel{!}{=} -\frac{1}{3} Q(e_L) \, . \end{align}

Analogously, we can derive a relation between $e_R^c$, $u_L$ and $u_R^c$. Thus $Q_{\text{proton}}+Q_{\text{electron}}= \mathcal{O}(10^{-20})$ is no longer a miracle, but rather a direct consequence of of the embedding of $G_{SM}$ in an enlarged gauge symmetry.

The Standard Model Coupling Strengths

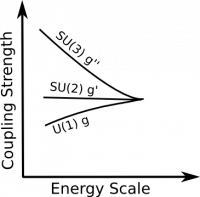
The standard model contains three gauge couplings, which are very different in strength. Again, this is not a real problem of the standard model, because we can simply put these values in by hand. However, GUTs provide a beautiful explanation for this difference in strength. A simple group $G_{GUT}$ implies that we have only one gauge coupling as long as $G_{GUT}$ is unbroken. The gauge symmetry $G_{GUT}$ is broken at some high energy scale in the early universe. Afterwards, we have three distinct gauge couplings with approximately equal strength. The gauge couplings are not constant, but depend on the energy scale. The RGEs for a gauge coupling depend on the number of particles that carry the corresponding charge. Gauge bosons have the effect that a given gauge coupling becomes stronger at lower energies and fermions have the opposite effect. The adjoint of $SU(3)$ is $8$-dimensional and therefore we have $8$ corresponding gauge bosons. In contrast the adjoint of $SU(2)$ is $3$-dimensional and thus we have $3$ gauge bosons. For $U(1)$ there is only one gauge boson. As a result for $SU(3)$ the gauge boson effect dominates and the corresponding gauge coupling becomes stronger at lower energies. For $SU(2)$ the fermion and boson effect almost cancel each other and thus the corresponding gauge coupling is approximately constant. For $U(1)$ the fermions dominate and the $U(1)$ gauge coupling becomes much weaker at low energies. This way GUTs provide an explanation why strong interactions are strong and weak interactions are weak.

Lightness of the Neutrino Masses
A quite generic implication of grand unification is small neutrino masses through the type-1 seesaw mechanism. Models based on the popular $SO(10)$ or $E_6$ groups contain automatically a right-handed neutrino $\nu_R$. As a result of the breaking chain this standard model singlet $\nu_R$ gets a superheavy mass $M$. After the last breaking step $G_{SM}\rightarrow SU(3)_C \times U(1)_Y$ the right-handed and left-handed neutrinos mix. This yields a suppressed mass of the left-handed neutrino of order $\frac{m^2}{M}$, where $m$ denotes a typical standard model mass.
Matter-Antimatter Asymmetry
GUTs provide a natural framework to explain the observed matter-antimatter asymmetry in the universe. As already noted above a general implication of GUTs is that protons are no longer stable. Formulated differently, GUTs allow baryon number-violating interactions. This is one of three central ingredients, known as Sakharov conditions, needed to produce more baryons than antibaryons in the early universe. Thus, as D. V. Nanopoulos put it, "if the proton was stable it would not exist".

“GUTs are the most attractive conjecture for the large scale picture of particle physics. GUT is not the Standard Model (SM), is beyond the SM, but is the most standard physics beyond the SM. Most of us think that there should be something like a GUT.”Altarelli

FAQ

Why does a simple group mean that we have just one coupling?
In QFT we get for each simple group a coupling. In contrast consider the couplings in a non-simple group:

This Lagrangian is actually invariant under a larger U(2) = U(1) × SU(2) symmetry. But, as we will come to understand, there is no point in considering non-simple groups such as U(N) in quantum field theory. For example, in a gauge theory the coupling constants for the U(1) and SU(2) subgroups will in general be different; even if we set them equal at one scale, they will run differently. Moreover, the U(1) symmetry in Lagrangians such as Eq. (25.1) will often be violated by a quantum effect called an anomaly, to be discussed in Chapter 30. Thus, we will restrict attention to the simple SU(N) subgroups.

from Quantum Field Theory by Schwartz

Do the Standard Model gauge couplings really do not unify?
No! The hypercharge normalization is not fixed in the standard model and if we choose a normalization $k_Y= 11/3$, the gauge couplings meet perfectly around $10^{17}$ GeV. Two gauge couplings $g_2$ and $g_3$ always meet at a point as long as they aren't parallel and because the normalization of $g_1$ isn't fixed we can adjust it appropriately. (This is mentioned, for example, here: https://arxiv.org/pdf/0903.3929.pdf)

A nice overview of how the hypercharge normalization is fixed for different GUT groups, see Table 1 in https://arxiv.org/pdf/hep-ph/0606012.pdf

History

Criticism

"Physics is littered with the corpses of dead unified field theories." Freeman Dyson

"The bad news is that those people who went off to detect proton decay never found it! It became clear in the mid-1980s that the proton lifetime was at least $10^{32}$ years or so, much larger than what the SU(5) theory most naturally predicts. Of course, if one is desperate to save a beautiful theory from an ugly fact, one can resort to desperate measures. For example, one can get the SU(5) model to predict very slow proton decay by making the grand unification mass scale large. Unfortunately, then the coupling constants of the strong and electroweak forces don't match at the grand unification mass scale. This became painfully clear as better measurements of the strong coupling constant came in." from This Week's Finds in Mathematical Physics (Week 119) by John Baez

“People can construct models with higher symmetries and stand on their nose and try to avoid proton decay,” Nanopoulos said. “OK, you can do it, but … you cannot show it to your mother with a straight face.” https://www.quantamagazine.org/20161215-proton-decay-grand-unification/

Major Questions still unsolved in GUTs

  • The Hierarchy Problem, i.e. why $M_W/M_{GUT} <10^{-12}$.
  • The strong CP problem.
  • The cosmological constant problem.
  • The absence of gravity.
  • The family repetition problem, i.e. why are there three families.
  • The fermion mass spectrum.

GUTs have nothing to say on these matters.