Variational Calculus
Why it is interesting?
Variational calculus is the alternative to the usual calculus methods when we want to find functions that minimize something. As an analogy, usually when we search for the extrema of a function, we differentiate the function, set the derivative of the function to zero and find the point that yields the extrema. Similar results can be computed by using variational calculus.In variational calculus we find extrema of functionals which are functions of functions with respect some function (instead of variable). This is extremely important for the Lagrangian formalism.
Variational calculus of the catenary
'Catenary' is the name of the curve that represents the shape of a hanging chain. The catenary problem is a problem in statics. Each point of the hanging chain is motionless, as if all points of the chain are anchored.
At the anchor point the tension in the chain can be calculated as follows: the weight tugging at that point is the total weight of the chain. That total weight is tugging in vertical direction. Then the horizontal component of the chain tension is given by the local angle of the chain.
Given that the chain is motionless this evaluation can be repeated everywhere along the length of the chain, from the top anchor point to the lowest point, which is in the middle. This means that the state of static equilibrium of the catenary can be expressed in the form of a differential equation. I will refer to this way of obtaining a differential equation as 'the direct approach'.
This raises the question: is it fortuitous that the problem of finding the shape of a catenary can be stated as a differential equation?
In fact this is a general property, and the underlying reason for that was first recognized by the mathematician Jacob Bernoulli. This was in the context of the Brachistochrone problem.
Brachistochrone problem
When Johann Bernoulli had presented the Brachistochrone problem to the mathematicians of the time Jacob Bernoulli was among the few who was able to find the solution independently. The treatment by Jacob Bernoulli is in the Acta Eruditorum, May 1697, pp. 211-217
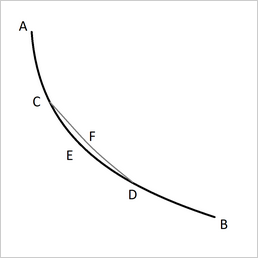
Jacob opens his treatment with an observation concerning the fact that the curve that is sought is a minimum curve.
Lemma. Let ACEDB be the desired curve along which a heavy point falls from A to B in the shortest time, and let C and D be two points on it as close together as we like. Then the segment of arc CED is among all segments of arc with C and D as end points the segment that a heavy point falling from A traverses in the shortest time. Indeed, if another segment of arc CFD were traversed in a shorter time, then the point would move along ACFDB in a shorter time than along ACEDB, which is contrary to our supposition.
The historical statement of Jacob's Lemma was specifically for the Brachistochrone problem. Generalization of it is straightforward. It makes no difference whether the extremum condition is a minimum condition or a maximum condition.
If the solution is an extremum for the entire curve then it is also an extremum for any sub-section of the curve, down to infinitisimally short subsections.
It follows that if a problem can be stated in variational form, then if a solution exists there exists a way to restate the condition in the form of a differential equation.
In the case of the catenary the static equilibrium can be cast in terms of minimizing potential energy. The middle of the chain tends to pull the sides inward. When the sides are pulled inward they are also raised, which increases the potential energy of the sides. So the middle can pull the sides inward only so much. The catenary is an extremum of the global potential energy of the chain.
The same reasoning, mirrored, applies in the case of a catenary arch. In the case of a catenary arch the extremum is a maximum of potential energy.
For the catenary the variational problem then is: find the curve such that the derivative of the total potential energy with respect to variation is zero. Notice that since the evaluation looks exclusively at the derivative it is not known whether the extremum is a minimum or a maximum. This does not present any problem; the catenary and the catenary arch have the same shape; the shape is the solution to the problem. Whether the extremum condition is a minimum condition or a maximum condition is immaterial.
The two approaches, direct approach and variational approach, converge; the two approaches arrive at the same differential equation.
Euler-Lagrange equation
The strategy of finding a solution to a problem in variational calculus is to find the way to restate the problem in terms of differential calculus.
The Euler-Lagrange equation is the implementation of that strategy. The derivation of the Euler-Lagrange equation does not make any assumption about the nature of the variational problem. If the solution to the variational problem satisfies an extremum condition then that solution will satisfy the corresponding Euler-Lagrange equation. Hence to find the solution to the variational form it suffices to find the solution to the corresponding Euler-Lagrange equation.
The existence of the Euler-Lagrange equation is in itself mathematical proof that any problem in variatioal calculus can be restated as a problem in differential calculus. As stated in the previous paragraph: the derivation of the Euler-Lagrange equation is completely general since it requires a single assumption only: that the solution to the variational problem satisfies an extremum condition.
Concrete
What we know from Calculus
On calculus, when we want to find the extremum of a function, we use the derivative:
We differentiate the function $f(x)$, then demand that the resulting derivative vanishes: $$\frac{d f(x)}{dx} \stackrel{!}{=} 0 , $$ if we solve for $x$, we find an critical point, for this function $f$
Concept of Variational Calculus
Instead of a function $f$ that takes numbers to numbers, the object of interest is a functional, a function of functions of sorts. To find the stationary functions of the functionals, we need to change a bit the differentiation process, and we use the functional derivative or variational derivative, and we equate the result to zero.
In the same way that the to find the extrema of a function one needs to solve a system of algebraic equation, the result of a variational derivative is a system of differential equations, these being ordinary or partial differential equations, depending on the function space being search.
This is the recipe of the variational problem
References
- Calculus of Variations, Gelfand and Fomin
- Calculus of Variations by MacCluer.
Abstract
See Karen Uhlenbeck and the Calculus of Variations by Simon Donaldson
Quotes
Another way of saying a thing is least is to say that if you move the path a little bit at first it does not make any difference. Suppose you were walking around on hills – but smooth hills, since the mathematical things involved correspond to smooth things – and you come to a place where you are lowest, then I say that if you take a small step forward you will not change your height. When you are at the lowest or at the highest point, a step does not make any difference in the altitude in first approximation, whereas if you are on a slope you can walk down the slope with a step and then if you take the step in the opposite direction you walk up. That is the key to the reason why, when you are at the lowest place, taking a step does not make much difference, because if it did make any difference then if you took a step in the opposite direction you would go down. Since this is the lowest point and you cannot go down, your first approximation is that the step does not make any difference. We therefore know that if we move a path a little bit it does not make any difference to the action on a first approximation. "The Character of Physical Law" by R. Feynman