Solitons

Why is it interesting?

Feynman diagrams do not describe everything that can happen in a quantum field theory. There can be classical solutions of the field equations that describe larger lumps of field excitations that aren't describable by Feynman diagrams.

Classical solutions of the field equations with finite energy are called solitons.

Such solutions are important to describe, for example, the vacuum of a theory. A famous example is the QCD vacuum which can only understand with the help of instantons.

In addition, there is an old dream that all elementary particles could be explained as topological solitons. (There are lots of problems with this idea, but at least, instantons come somewhat close.)

While solitons are rare in particle physics, they are found frequently in condensed matter physics.

Important examples of solitons are:

Soliton equations are special, but they are by no means unimportant; they arise in such diverse areas of applied science as hydrodynamics, nonlinear optics, plasma dynamics, meteorology, Josephson type superconductive devices, nonlinear acoustics, oceanography, domain wall dynamics, dislocation theory, nonlinear electric filters, and in the theory of elementary particles.

http://garfield.library.upenn.edu/classics1979/A1979HF81700001.pdf

Layman

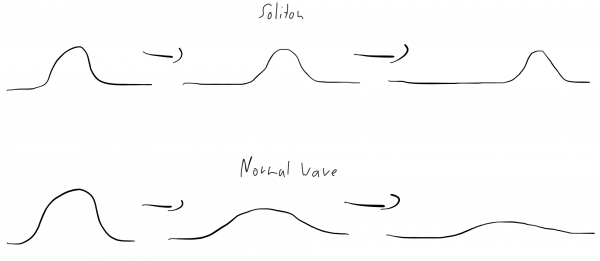
A soliton is a curious type of stable wave. Usually, waves vanish after some time. Think of a stone that gets thrown into some water. The stone will cause waves. At first, these waves will be large, but quickly get smaller and smaller until they are no longer visible. The waves flattens out. This process is known as dissipation.

In contrast, a soliton does not dissipate its energy but remains its form over a long time, possibly infinitely.

Before suggesting why the paper has been so often cited, it is appropriate to explain what the term soliton means. As coined by Zabusky and Kruskal, this term is generic for special solitary wave solutions of certain nonlinear wave equations.

What then is a solitary wave? It is a pulse-like wave that travels with constant speed and shape; the effects of dispersion on the wave shape are just balanced by those of nonlinearity. There is just enough yin for the yang; it is a dynamically self-sufficient object, a ‘thing.’

Solitons are solitary waves that preserve their speeds and shapes after mutual collision. They play a role in the construction of complete solutions for the nonlinear wave equation that corresponds to the role played by Fourier components in the construction of solutions for linear wave equations.

http://garfield.library.upenn.edu/classics1979/A1979HF81700001.pdf

“A solitary wave travels without changing its shape, size, or, speed” J. Scott Russell, “Report on waves”

Student

A soliton is a wave-packet that keeps a stable shape while propagating. The defining features of a soliton are:

  1. A soliton is of permanent form, which basically means that they are static (=time independent) solutions of the field equations
  2. A soliton is localized within a finite region. In other words, its energy and spatial size is finite.
  3. When a soliton interacts with another soliton it emerges from the collision in exactly the same shape it had before. Only a phase shift is possible.

Solitons are stable through the interplay of dissipation and non-linearity of the underlying wave equations.

  • Dissipation happens because a wave packet is a superposition of waves with different wave-lengths and usually waves with different wave-lengths travel with different velocities.
  • Non-linearity of the wave equations can result in waves that get steeper over time. A good example are the waves that can be observed at a beach.

Recommended Textbooks

<