Add a new page:
This is an old revision of the document!
Given a field bundle […], we know what type of quantities the corresponding fields assign to a given spacetime point. Among all consistent such field configurations, some are to qualify as those that “may occur in reality” if we think of the field theory as a means to describe parts of the observable universe. Moreover, if the reality to be described does not exhibit “action at a distance” then admissibility of its field configurations should be determined over arbitrary small spacetime regions, in fact over the infinitesimal neighbourhood of any point. This means equivalently that the realized field configurations should be those that satisfy a specific differential equation, hence an equation between the value of its derivatives at any spacetime point.
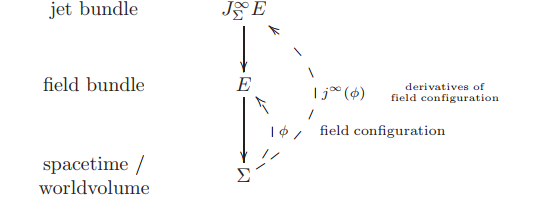
In order to formalize this, it is useful to first collect all the possible derivatives that a field may have at any given point into one big space of “field derivatives at spacetime points”. This collection is called the jet bundle of the field bundle.https://ncatlab.org/nlab/show/field+%28physics%29#AFirstIdeaOfQuantumFields
The dynamics of a field theory is specified by an equation of motion, a partial differential equation for such sections. Since differential equations are equations among all the derivatives of such sections, we consider the spaces that these form: the jet bundle $J^\infty_\Sigma E $ is the bundle over $\Sigma$ whose fiber over a point $\sigma \in \Sigma$ is the space of sections of $E$ over the infinitesimal neighbourhood $\mathbb{D}_\sigma$ of that point:
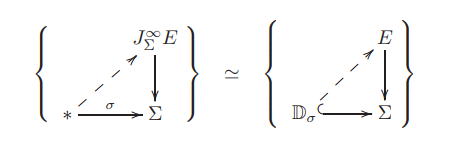
Therefore every section $\phi$ of $E$ yields a section $j^\infty(\phi)$ of the jet bundle, given by $\phi$ and all its higher order derivatives.
Accordingly, for $E, F$ any two smooth bundles over $\Sigma$, then a bundle map
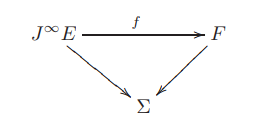
encodes a (non-linear) differential operator $D_f : \Gamma_\Sigma(E) \longrightarrow \Gamma_\Sigma(F)$ by sending any section $\phi$ of $E$ to the section $f \circ j^\infty(\phi)$ of $F$.https://arxiv.org/abs/1601.05956