Add a new page:
$SO(3,1)$
For a perfect intuitive introduction to the Lorentz group, see this video by minutephyiscs.
Definition of the Lorentz transformations
It follows from the postulates of special relativity that $d s^2 = \eta^{\mu \nu} dx_\mu dx_\nu$ stays exactly the same in all inertial frames of reference: \begin{equation} ds'^2 = dx'_\mu dx'_\nu \eta^{\mu\nu} = ds^2 = dx_\mu dx_\nu \eta^{\mu\nu} \, ,\end{equation} where $\eta^{\mu\nu}$ is the Minkowski metric.
We denote a generic transformation that takes us to another frame with $\Lambda$ and the transformed coordinates $dx_\mu'$:
\begin{equation} \label{eq:lorentztrafo1} dx_\mu \rightarrow dx'_\mu=\Lambda^{ \ \sigma}_{\mu} dx_\sigma. \end{equation} Then we can write the invariance condition from above as: \begin{align} (ds)^2 &= (ds')^2 \notag \\ \rightarrow dx \cdot dx &\stackrel{!}{=} dx' \cdot dx' \notag \\ \rightarrow dx_\mu dx_\nu \eta^{\mu\nu} &\stackrel{!}{=} dx'_\mu dx'_\nu \eta^{\mu\nu} \underbrace{=} \Lambda^{ \ \sigma}_{ \mu} dx_\sigma \Lambda^{ \ \gamma}_{ \nu} dx_\gamma \eta^{\mu\nu} \notag \\ \underbrace{\rightarrow} dx_\mu dx_\nu \eta^{\mu\nu} &\stackrel{!}{=} \Lambda^{ \ \mu}_{ \sigma} dx_\mu \Lambda^{ \ \nu}_{ \gamma} dx_\nu \eta^{\sigma\gamma} \notag \\ \underbrace{\rightarrow}_{\text{Because the equation holds for arbitrary } dx_\mu} \eta^{\mu\nu} &\stackrel{!}{=} \Lambda^{ \ \mu}_{ \sigma} \eta^{\sigma \gamma} \Lambda^{ \ \nu}_{ \gamma} \end{align}
Or written in matrix notation
\begin{equation} \label{eq:lorentztrafodefequation} \eta = \Lambda^T \eta \Lambda \end{equation}
This is the condition that transformations $\Lambda$ which take us from one frame to another allowed frames of reference must fulfill. Such transformations are called Lorentz transformations and the equation can be taken as a definition of Lorentz transformations. Formulated differently, the Lorentz transformations are defined as all those transformations that leave the Minkowski metric unchanged.
Explicit form of the Lorentz transformations
Rotations First, we note that the rotation matrices of 3-dimensional Euclidean space that only act on space and not on time, fulfil the defining condition. This follows because the spatial part ($\mu=1,2,3$) of the Minkowski metric is proportional to the $3 \times 3$ identity matrix. Thus for transformations that only modify space, we get from the condition $\eta = \Lambda^T \eta \Lambda$ that
\[-R^T I_{3 \times 3} R =- R^T R \stackrel{!}{=} - I_{3 \times 3} \] \[\rightarrow R^T I_{3 \times 3} R =R^T R \stackrel{!}{=} I_{3 \times 3} . \] This is exactly the defining condition of the group $O(3)$. Together with the condition \[ \det(\Lambda) \stackrel{!}{=} 1 \] these are the defining conditions of the group $SO(3)$, which describes three-dimensional rotations. We conclude that one type of Lorentz transformation is given by \[ \Lambda_{\mathrm{rot }}= \begin{pmatrix} 1 & \\ & R_{3 \times 3} \end{pmatrix} \] with the usual rotation matrices $R_{3 \times 3}$:
\begin{eqnarray} & & R_x(\phi) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\phi & \sin\phi \\ 0 & -\sin\phi & \cos\phi \end{pmatrix} \label{eq:rotx} \\ & & R_y(\psi) = \begin{pmatrix} \cos \psi & 0 & -\sin\psi \\ 0 & 1 & 0 \\ \sin\psi & 0 & \cos\psi \end{pmatrix} \label{eq:roty} \\ & & R_z(\theta) = \begin{pmatrix} \cos \theta & \sin \theta & 0 \\-\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \label{eq:rotz} \end{eqnarray}
Boosts
To investigate all other transformations which transform time and space we start, as usual in Lie theory, with an infinitesimal transformation \begin{equation} \Lambda^{\mu}_{\rho} \approx \delta^{\mu}_{\rho}+ \epsilon K^{\mu}_{\rho}. \end{equation} We put this now into the defining condition $\eta = \Lambda^T \eta \Lambda$ and get \[\Lambda^{\mu}_{\rho} \eta_{\mu \nu} \Lambda^{\nu}_{\sigma} \stackrel{!}{=} \eta_{\rho \sigma} \] \[ \rightarrow ( \delta^{\mu}_{\rho}+ \epsilon K^{\mu}_{\rho} ) \eta_{\mu \nu} (\delta^{\nu}_{\sigma}+ \epsilon K^{\nu}_{\sigma}) \stackrel{!}{=} \eta_{\rho \sigma} \] \[ \rightarrow \eta_{\rho \sigma} + \epsilon K^{\mu}_{\rho}\eta_{\mu \sigma} + \epsilon K^{\nu}_{\sigma} \eta_{\rho \nu} + \underbrace{\epsilon^2 K^{\mu}_{\rho}\eta_{\mu \nu} K^{\nu}_{\sigma}}_{ \approx 0 \text{ because } \epsilon \text{ is infinitesimal }\rightarrow \epsilon^2 \approx 0} = \eta_{\rho \sigma} \] \begin{equation}\rightarrow K^{\mu}_{\rho}\eta_{\mu \sigma} + K^{\nu}_{\sigma} \eta_{\rho \nu} = 0 \end{equation}
or in matrix notation
\begin{equation} \label{eq:boost4d} K^T \eta = - \eta K. \end{equation}
A transformation that fulfill this equation is called a boost. A boost takes us from one frame to another frame that moves with a different velocity. Explcitly, such transformations can be described by
\begin{equation} \Lambda_x = \begin{pmatrix} \cosh(\phi)&i\sinh(\phi) & 0 & 0\\ i\sinh(\phi)& \cosh(\phi) &0 &0 \\ 0&0&1&0 \\ 0&0&0&1 \end{pmatrix} \end{equation}
\begin{equation} \Lambda_y = \begin{pmatrix} \cosh(\phi)& 0 & i\sinh(\phi) & 0\\ 0 & 1 &0 &0 \\ i\sinh(\phi)& 0 & \cosh(\phi) &0 \\ 0&0&0&1 \end{pmatrix} \end{equation}
\begin{equation} \label{eq:boostexplicitz-direction} \Lambda_z = \begin{pmatrix} \cosh(\phi)&0 & 0 & i\sinh(\phi)\\ 0 &1 &0 &0 \\ 0&0&1&0 \\ i\sinh(\phi)& 0 &0 &\cosh(\phi) \end{pmatrix}. \end{equation}
Representations of the Lorentz group
At the heart of the representation theory of the Poincare group is the representation theory of the proper orthochronous Lorentz group $SO(1,3)^{\uparrow}$. We can concentrate on this subset of the Lorentz group, because the Lorentz group can be decomposed as follows:
\begin{equation} \label{eq:completedef03} O(1,3) = \{ SO(1,3)^{\uparrow}, \Lambda_P SO(1,3)^{\uparrow} , \Lambda_T SO(1,3)^{\uparrow} , \Lambda_P \Lambda_T SO(1,3)^{\uparrow} \} \, .\end{equation} These four disconnected components are connected through parity transformations $\Lambda_P$ and time-reversal transformations $\Lambda_T$. This means in practice that once we have derived the representations of $SO(1,3)^{\uparrow}$, we get the representations of the other components (and hence of the full Lorentz group) simply by acting with the corresponding representations of the parity and time-reversal transformations on our representations.
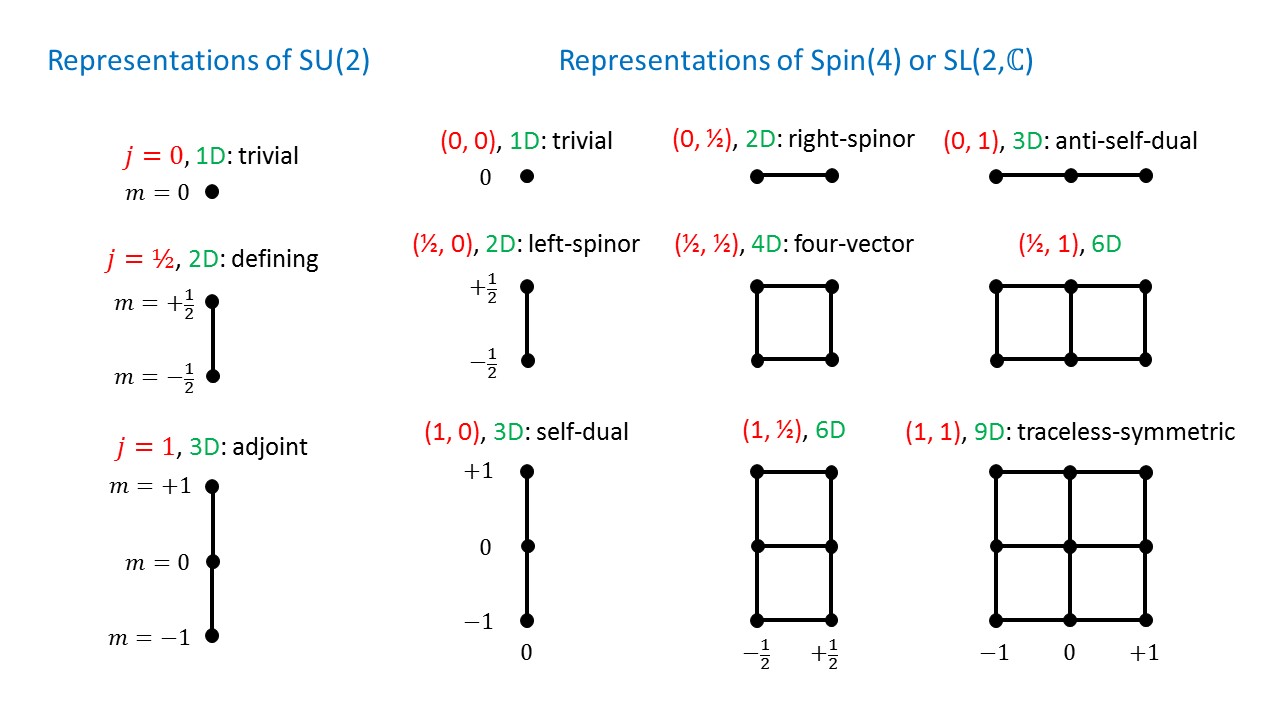
The lowest-dimensional irreducible representation of the Lorentz group are
| Name | Dimension | $(j_L,j_R)$ |
|---|---|---|
| scalar | 1 | $(0,0)$ |
| left-chiral spinor | 2 | $(\frac{1}{2},0)$ |
| right-chiral spinor | 2 | $(0,\frac{1}{2})$ |
| vector | 4 | $(\frac{1}{2},\frac{1}{2})$ |
| self dual antisymmetric | 3 | $(1,0)$ |
| anti-self dual antisymmetric | 3 | $(0,1)$ |
| traceless symmetric | 9 | $(1,1)$ |
Moreover, in physical application the reducible Dirac representation is important: $$(\frac{1}{2},0) \oplus (0,\frac{1}{2}) .$$ This means, the famous Dirac spinors transform according to this reducible representation. Further, we have $$(\frac{1}{2},0) \otimes (0,\frac{1}{2}) = (\frac{1}{2},\frac{1}{2}) $$ $$(\frac{1}{2},0) \otimes (\frac{1}{2},0) = (1,0) \oplus (0,0). $$
The adjoint representation of the Lorentz group is $6$-dimensional and given by $$(1,0) \oplus (0,1) .$$ (Source: page 42 in http://solenodonus.com/file/electromagnetic-duality-for-children.pdf )
Derivation of the Representations of the Lorentz Group
To derive the representations of $SO(3,1)$, we employ Weyl's unitary trick. This trick allows us to derive irreducible non-unitary representations of the Lorentz group, by starting with the known unitary representations of $SO(4)$. However this
"works only for the finite or spin representations and for the Lorentz group these by no means exhaust all representations." from INVARIANCE IN ELEMENTARY PARTICLE PHYSICS BY N . KEMMER et. al.
Take note that this application of Weyl's unitary trick is so important that is has its own name: Wick rotation. This means the Weyl unitary trick that deformes $SO(3,1) \rightarrow SO(4)$ is called a Wick rotation. (c.f. p. 28 in http://math.ucr.edu/home/baez/thesis_wise.pdf)
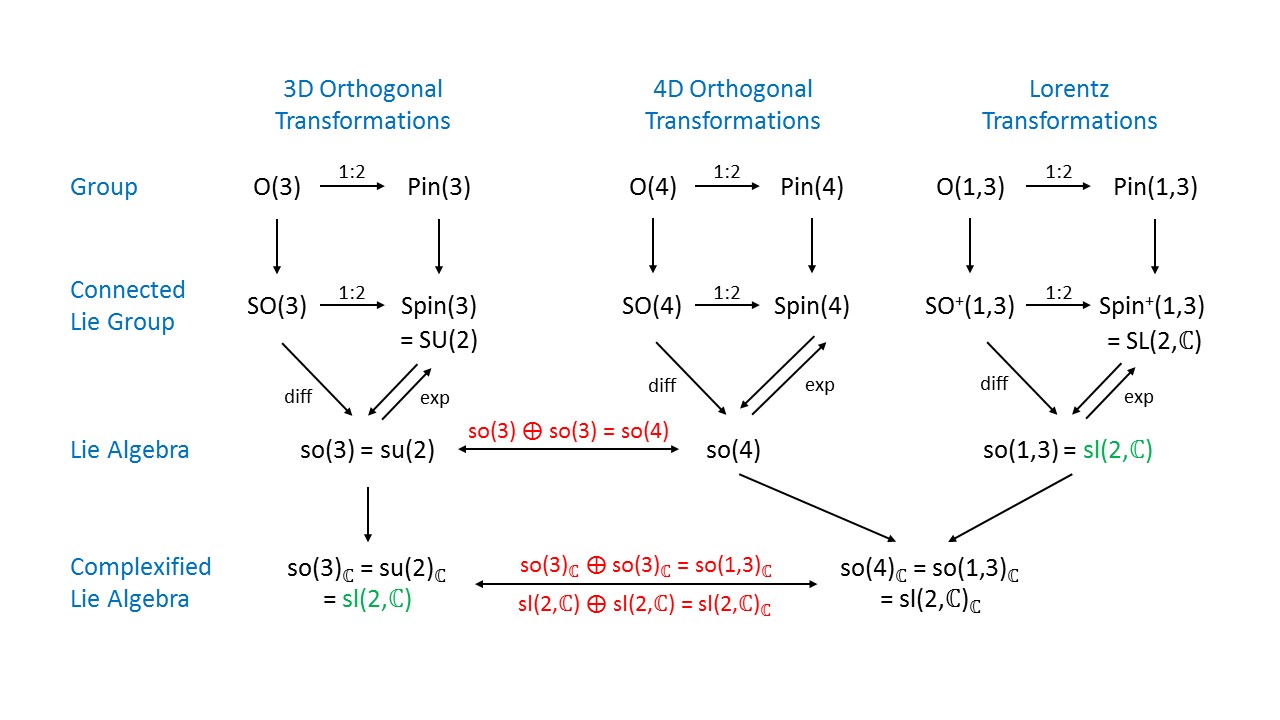
We can use that the Lie algebra of $SO(4)$, denoted by $\mathfrak{so}(4)$, is isomorphic to to the Lie algebra $\mathfrak{su}(2)\times \mathfrak{su}(2)$. (In fact, $SU(2) \times SU(2)$ is the double cover of $SO(4)$ and therefore we have the isomorphism $SO(4) \simeq SU(2) \times SU(2) / \mathbb{Z}_2$).
The understand this explicitly, we write down the commutation relations of the Lorentz group:
\begin{equation} \label{eq:JJcommutator} [J_i,J_j]=i \epsilon_{ijk} J_k \end{equation} \begin{equation} \label{eq:JKcommutator} [J_i,K_j]=i \epsilon_{ijk} K_k \end{equation} \begin{equation} \label{eq:KKcommutator} [K_i,K_j]=- i \epsilon_{ijk} J_k \, ,\end{equation} where $J_i$ are the generators of rotations and $K_i$ are the generators of boosts. This means, a general Lorentz transformation can be written as \begin{equation} \Lambda = {\mathrm{e }}^{i \vec J \cdot \vec \theta + i \vec K \cdot \vec \Phi} .\end{equation}
Now, we employ Weyl's unitary trick and multiply the boost generators with $i$: $K_i \rightarrow i K_i$. This is a deformation of the Lie algebra. The deformed Lie algebra is simply the Lie algebra $\mathfrak{so}(4)$. Then, we can introduce the following new generators from the old ones \begin{equation} \label{eq:defN} N^{+}_i \equiv \frac{1}{2}(J_i +i K_i) \end{equation} \begin{equation} N^{-}_i \equiv \frac{1}{2}(J_i -i K_i) . \end{equation} (Another point of view is that we here complexify the Lorentz algebra: $\mathfrak{so}(3,1) \rightarrow \mathfrak{so}(3,1)_\mathbb{C}$, because we now allow complex linear combinations of the generators).
The commutation relations for these new set of generators are \begin{equation} [N^{+}_i,N^{+}_j]=i \epsilon_{ijk} N^{+}_k \end{equation} \begin{equation} [N^{-}_i,N^{-}_j]=i \epsilon_{ijk} N^{-}_k \end{equation} \begin{equation} [N^{+}_i,N^{-}_j]= 0 \, . \end{equation} Thus, we can see that we have here simply two times the Lie algebra $\mathfrak{su}(2)$. We conclude that through the introduction of the new set of generators $N^{+}_i $ and $N^{-}_i $, we have found an isomorphism between $\mathfrak{so}(4)$ and $\mathfrak{su}(2) \times \mathfrak{su}(2)$.
To summarize:
| $\mathfrak{so}(3,1)$ | Weyl Trick | $\mathfrak{so}(4) $ | $\mathfrak{su}(2) \times \mathfrak{su}(2)$ | |||||||||||||||||||||||||||||||
Take note that we have changed something fundamental through the Lie algebra deformation (the Weyl trick) $K_i \rightarrow i K_i$. The resulting complexified Lorentz algebra $\mathfrak{so}(3,1)_\mathbb{C}$ is isomorphic to $\mathfrak{sl}(2,\mathbb{C})_\mathbb{C}$. Thus by deriving the representations of this Lie algebra we get the representations of the group $SL(2,\mathbb{C})$. $SL(2,\mathbb{C})$ is the group of complex $2 \times 2$ matrices with unit determinant. The difference between $SL(2,\mathbb{C}$ and $SU(2)$ is that the former group contains transformations that aren't necesarrily unitary). This group is the universal cover of the Lorentz group. ( $SL(2,\mathbb{C})$ double covers $SO(3,1)^\uparrow$. This means there is a map that maps $SL(2,\mathbb{C})$ elements to $SO(3,1)^\uparrow$ elements and this map is not one-to-one, but two-to-one. Two elements of $SL(2,\mathbb{C})$ get mapped to the same element of $SO(3,1)^\uparrow$.) Therefore by studying the irreducible representations of $\mathfrak{so}(3,1)_\mathbb{C}$, we do not only get representations of the Lorentz group, but additional representations. One additional representations is, for example, the famous spin $1/2$ representation that we use to describe fermions. This means the representations of the Lorentz group aren't enough to describe all fundamental systems. We actually need to representations of the double cover of the Lorentz group to describe fermions.
See also https://apps.carleton.edu/curricular/math/assets/symmetrycompsproject.pdf
"the Lorentz group is not compact because it contains boosts (hence all unitary representations are infinite-dimensional); and it is not simply connected because it contains rotations (so we need to study the representations of its universal covering group SL(2, C))."http://www.staff.uni-giessen.de/~gd1632/2014-hadron-physics/hadron-app-2.pdf
"physical experiments show that a connected double cover of the Poincare is more appropriate in creating the symmetry group actual spacetime." https://apps.carleton.edu/curricular/math/assets/symmetrycompsproject.pdf
The usual way how the representation theory of the Lorentz algebra is explained makes use of the complexification of the Lie algebra and the fact that the complexified Lorentz algebra looks like two copies of the $SU(2)$ Lie algebra $\mathfrak{su}(2)$: $$ \mathfrak{so}(3,1)\otimes \mathbf C = \mathfrak{sl}(2,\mathbf C) + \mathfrak{sl}(2,\mathbf C) $$ However, the complexification of the Lie algebra of an orthogonal group is the same thing no matter what signature you start with $$ \mathfrak{so}(3,1)\otimes \mathbf C =\mathfrak{so}(4)\otimes \mathbf C =\mathfrak{so}(2,2)\otimes \mathbf C = \mathfrak{sl}(2,\mathbf C) + \mathfrak{sl}(2,\mathbf C) $$
The Lie algebras we are interested in in physics are real Lie algebras. By restricting to real Lie algebras, we can still consider different real forms of a given Lie algebra: \begin{align} \mathfrak{so}(3,1)&=\mathfrak{sl}(2,\mathbf C) \\ \mathfrak{so}(4)&=\mathfrak {su}(2) + \mathfrak {su}(2) \\ \mathfrak{so}(2,2)&=\mathfrak{sl}(2,R) +\mathfrak{sl}(2,R) \end{align}
Source: http://www.math.columbia.edu/~woit/wordpress/?p=9222
See also, section 5.5 at page 79 in http://www.math.columbia.edu/~woit/QM/qmbook.pdf
Graphical Summary
The picture below shows the weight diagrams of some important irreducible representations of the (double cover of the) Lorentz group (right) and, for comparison, some irreducible representations of $SU(2)$ (left). For a more detailed explanation of this picture see Fun with Symmetry.
The following diagram illustrates the relationship between the groups of rotation $O(3)$ and $O(4)$, in 3D and 4D Euclidean space, respectively, and the Lorentz group $O(1,3)$. For a more detailed explanation of this diagram see Fun with Symmetry.
The Lorentz group is an important part of the fundamental spacetime symmetry group of the standard model, called the Poincare group.
It encodes the fact that physics should be the same in all frames of reference and additionally that the speed of light is the same in all such frames.
Understanding the representations is crucial for the standard model, because these representations are the tools that we need to describe elementary particles.