$$ \mathcal H=-J\sum_{\langle ij\rangle}S_iS_j$$

Ising Model

Intuitive

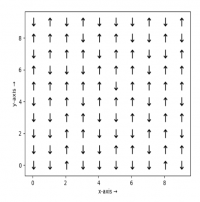
The Ising model consists of a linear chain (or lattice) where at each node we have an either an arrow that points upwards or an arrow that points downwards. The force between two neighboring lattice nodes depends on whether they point in the same direction or not.

Concrete

The Hamiltonian of the Ising model is: \begin{equation} \mathcal H=-J\sum_{\langle ij\rangle}S_iS_j\,,\label{HIsing} \end{equation} where the summation runs only over nearest-neighbor pairs $\langle ij\rangle$ on the lattice. $J$ is the interaction strength.

The statistical properties of the system are obtained from the corresponding partition function \begin{equation} Z=\sum_{\mathcal C} e^{-\beta E({\mathcal C})}\,, \end{equation} where the summation runs over all possible configurations $\mathcal C$ and $E({\mathcal C})$ denotes the energy of a given configuration. Moreover, $\beta\equiv 1/(k_B T)$ is the inverse temperature (temperature $T$ and Boltzmann constant $k_B$).

There is a second-order phase transition at temperature $T_c$. This phase transition is characterised by a high temperature phase with an average magnetization zero (disordered phase) and a low temperature phase with a non-zero average magnetization (ordered phase).

The Ising model is exactly solvable in one and two dimensions. In four-dimension, we can calculate the critical properties using the renormalization group.

  • The best introduction can be found in Critical point phenomena: universal physics at large length scales by Bruce, A.; Wallace, D. published in the book "The New Physics", edited by P. Davies.
  • Another great introduction can be found here.
  • See also An introduction to the Ising model by Barry A. Cipra, which is a good introduction for beginners.

The Ising model was originally devised as a simplified model of a ferromagnet, but is applicable also in a much broader sense. There is no need to refer to any ferromagnetic setup, but instead the Ising model can be used in a generalized sense.

Recommended Resources

  • A Python simulation of the 2D Ising model, can be downloaded here.

Abstract

Why is it interesting?

The Ising model is the simplest model with a critical point and thus ideal to understand notions like critical exponents and the renormalization group in a simplified setup.

The Ising Model has been called the Drosophila of condensed matter physics: a simple and well understood case on which the phenomena associated with phase transitions can be studied. http://philsci-archive.pitt.edu/8339/1/Is_more_different_2006.pdf

FAQ

Where does the Ising model come from?
Source: Where do quantum field theories come from? by McGreevy
In what forms does the Ising model appear?
Source: Where do quantum field theories come from? by McGreevy

Abstract

←-

History