Seesaw Models

Intuitive

Concrete

Seesaw scenarios can be understood systematically by looking at the Weinberg operator. The Weinberg operator $\frac{1}{\Lambda} LL \phi \phi$ is a (non-renormalizable) dimension-5 operator that yields nonzero masses for the neutrinos. Since it is an dimension-5 operator, it is suppressed by some large mass scale $\Lambda$. The origin of the Weinberg operator can be understood in terms of concrete seesaw scenarios (UV-completions).

There are three seesaw scenarios that yield the Weinberg operator in the low-energy limit when we integrate out all heavy fields and thus use an effective field theory approach. In particular, we can distinguish different scenarios depending on how we understand the contractions of our $SU(2)_L$ multiplets:

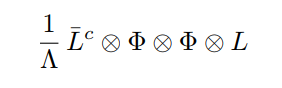
In terms of Feynman diagrams, the three scenarios can be understood as follows:

Here, $N_R$ denotes a heavy right-handed ($SU(2)_L$ singlet) neutrino, $\Delta^0$ the neutral component of an $SU(2)_L$ scalar triplet and $\Sigma_R^0$, the neutral component of a fermionic $SU(2)_L$ triplet.

A slightly different way of understanding the seesaw scenarios in terms of Feynman diagrams is (source):

Great reviews are:

• Low energy effects of neutrino masses by A. Abada, C.Biggio, F. Bonnet, M.B. Gavela, T. Hambye
• The Effective Lagrangian for the Seesaw Model of Neutrino Mass and Leptogenesis by A. Broncano, M.B. Gavela, E. Jenkins

Abstract

Why is it interesting?

Seesaw models are extensions of the Standard Model of particle physics that aim to explain why neutrino masses are so tiny.