Dot Product / Scalar Product

Intuitive

Concrete

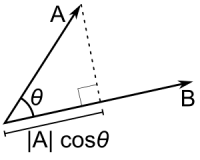
The [dot] product may be understood geometrically as the projection of one vector onto another, multiplied by the length of the vector that it is projected onto. If one takes the dot product of two vectors $\vec{a}$ and $\vec{b}$, we can apply this procedure to find the correct formula for the dot product:

Let's call the angle between the vectors $\varphi$. Then, the projection of $\vec{a}$ onto $\vec{b}$ is $|\vec{a}|\cos \varphi$. Multiplying by the length of $\vec{b}$ gives us $$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\varphi$$ This is the correct expression for the dot product. Of course, the dot product is symmetric so we might as well picture it as projecting $\vec{b}$ along $\vec{a}$. https://physics.stackexchange.com/a/111869/37286

• Vector Calculus: Understanding the Dot Product by Kalid Azad
• See also https://math.stackexchange.com/questions/348717/dot-product-intuition

Abstract

Why is it interesting?

The dot product is a tool that we can use to combine two vectors and get a number out. (That's why it is also called scalar product; scalar=number). This number tells us how much the first vector points in the direction of the second vector.

This is an extremely useful concept and used in almost any physical theory, like for example, electrodynamics. Moreover, many other important tools, like the divergence or the gradient are defined with the help of the dot product.