Renormalization Group

Intuitive

You are arranging the theory in such a way that only the right degrees of freedom, the ones that are really relevant to you, are appearing in your equations. I think that this is in the end what the renormalization group is all about. It's a way of satisfying the Third Law of Progress in Theoretical Physics, which is that you may use any degrees of freedom you like to describe a physical system, but if you use the wrong ones, you'll be sorry.

Why the Renormalization Group Is a Good Thing by Steven Weinberg

Concrete

Recommended Textbooks:

—-

Navier-Stokes Equation

The idea of nineteenth century hydrodynamic physics was that, upon systematically integrating out the high frequency, short wavelength modes associated with atoms and molecules, one ought to be able to arrive at a universal long wavelength theory of fluids, say, the Navier-Stokes equations, regardless of whether the fluid was composed of argon, water, toluene, benzene. […] The existence of atoms and molecules is irrelevant to the profound and, some might say, even fundamental problem of understanding the Navier-Stokes equations at high Reynold's numbers. We would face almost identical problems in constructing a theory of turbulence if quantum mechanics did not exist, or if matter first became discrete at length scales of Fermis instead of Angstroms.

Michael Fisher in Conceptual Foundations of Quantum Field Theory, Edited by Cao

Abstract

It is worthwhile to stress, at the outset, what a "renormalization group" is not! Although in many applications the particular renormalization group employed may be invertible, and so constitute a continuous or discrete, group of transformations, it is, in general, only a semigroup. In other words a renormalization group is not necessarily invertible and, hence, cannot be 'run backwards' without ambiguity: in short it is not a "group". The misuse of mathematical terminology may be tolerated since these aspects play, at best, a small role in RG theory.

Michael Fisher in Conceptual Foundations of Quantum Field Theory, Edited by Cao

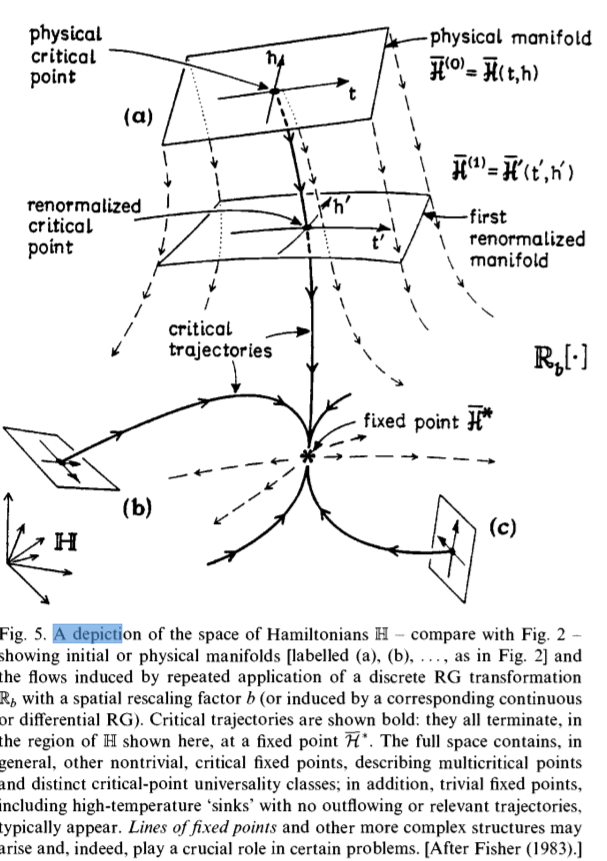
in Wilson's conception RG theory crudely says: "Well, (a) there is a flow in some space, $\mathcal{H}$, of Hamiltonians (or "coupling constants"); (b) the critical point of a system is associated with a fixed point (or stationary point) of that flow; ( c ) the flow operator - technically the RG transformation $\mathbb{R}$ - can be linearized about that fixed point; and (d) typically, such a linear operator (as in quantum mechanics) has a spectrum of discrete but nontrivial eigenvalues, say $\lambda_k$; then (e) each (asymptotically independent) exponential term in the flow varies as $e^{\lambda_k l}$ where $l$ is the flow (or renormalization) parameter and corresponds to a physical power law, say $|t|^{\phi_k}$, with critical exponent $\phi_k$ proportional to the eigenvalue $\lambda_k$." How one may find suitable transformations $\mathbb R$, and why the flows matter, are the subjects for the following chapters of our story. Just as quantum mechanics does much more than explain sharp spectral lines, so RG theory should also explain, at least in principle, (ii) the values of the leading thermodynamic and correlation exponents, $\alpha, \beta, \gamma, \delta, \nu, \eta$ (to cite those we have already mentioned above) and (iii) clarify why and how the classical values are in error, including the existence of borderline dimensionalities, like $d_x = 4$, above which classical theories become valid. Beyond the leading exponents, one wants (iv) the correction-to-scaling exponent $0$ (and, ideally, the higher-order correction exponents) and, especially, (v) one needs a method to compute crossover exponents, $\phi$, to check for the relevance or irrelevance of a multitude of possible perturbations. Two central issues, of course, are (vi) the understanding of universality with nontrivial exponents and (vii) a derivation of scaling: see (16) and (19). And, more subtly, one wants (viii) to understand the breakdown of universality and scaling in certain circumstances - one might recall continuous spectra in quantum mechanics - and (ix) to handle effectively logarithmic and more exotic dependences on temperature, etc.

Michael Fisher in Conceptual Foundations of Quantum Field Theory, Edited by Cao

Source: Conceptual Foundations of Quantum Field Theory, Edited by Cao

Recommended Papers:

Why is it interesting?

What does a JPEG have to do with economics and quantum gravity? All of them are about what happens when you simplify world-descriptions. A JPEG compresses an image by throwing out fine structure in ways a casual glance won't detect. Economists produce theories of human behavior that gloss over the details of individual psychology. Meanwhile, even our most sophisticated physics experiments can't show us the most fundamental building-blocks of matter, and so our theories have to make do with descriptions that blur out the smallest scales. The study of how theories change as we move to more or less detailed descriptions is known as renormalization. https://www.complexityexplorer.org/tutorials/67-introduction-to-renormalization

Furthermore, it forthrightly acknowledges the breadth of the RG approach citing as examples of problems implicitly or explicitly treated by RG theory:

(i) The KAM (Kolmogorov-Arnold-Moser) theory of Hamiltonian stability

(ii) The constructive theory of Euclidean fields

(iii) Universality theory of the critical point in statistical mechanics

(iv) Onset of chaotic motions in dynamical systems (which includes Feigenbaum's period-doubling cascades)

(v) The convergence of Fourier series on a circle

(vi) The theory of the Fermi surface in Fermi liquids (as described in the lecture by Shankar)

To this list one might well add:

(vii) The theory of polymers in solutions and in melts

(viii) Derivation of the Navier-Stokes equations for hydrodynamics

(ix) The fluctuations of membranes and interfaces

(x) The existence and properties of 'critical phases' (such as superfluid and liquid- crystal films)

(xi) Phenomena in random systems, fluid percolation, electron localization, etc.

(xii) The Kondo problem for magnetic impurities in nonmagnetic metals.

This last problem, incidentally, was widely advertised as a significant, major issue in solid state physics. However, when Wilson solved it by a highly innovative, numerical RG technique he was given surprisingly little credit by that community. It is worth noting Wilson's own assessment of his achievement: "This is the most exciting aspect of the renormalization group, the part of the theory that makes it possible to solve problems which are unreachable by Feynman diagrams. The Kondo problem has been solved by a nondiagrammatic computer method."

Earlier in this same passage, written in 1975, Wilson roughly but very usefully divides RG theory into four parts: (a) the formal theory of fixed points and linear and nonlinear behavior near fixed points where he especially cites Wegner (1972a, 1976), as did I, above; (b) the diagrammatic (or field-theoretic) formulation of the RG for critical phenomena 33 where the e expansion 34 and its many variants 35 plays a central role; © QFT methods, including the 1970-71 Callan-Symanzik equations 36 and the original, 1954 Gell-Mann-Low RG theory - restricted to systems with only a single, marginal variable 37 - from which Wilson drew some of his inspiration and which he took to name the whole approach. 38 Wilson characterizes these methods as efficient calculationally - which is certainly the case - but applying only to Feynman diagram expansions and says: "They completely hide the physics of many scales." Indeed, from the perspective of condensed matter physics, as I will try to explain below, the chief drawback of the sophisticated field-theoretic techniques is that they are safely applicable only when the basic physics is already well understood. By contrast, the general formulation (a), and Wilson's approach (b), provide insight and understanding into quite fresh problems.

Michael Fisher in Conceptual Foundations of Quantum Field Theory, Edited by Cao

If one is to pick out a single feature that epitomizes the power and successes of RG theory, one can but endorse Gallavotti and Benfatto when they say "it has to be stressed that the possibility of nonclassical critical indices (i.e., of nonzero anomaly $\eta$) is probably the most important achievement of the renormalization group."

Michael Fisher in Conceptual Foundations of Quantum Field Theory, Edited by Cao

FAQ

What are bare charges?

I said that poetically speaking, the bare charge of the electron is the charge we would see if we could strip off the electron’s virtual particle cloud. A somewhat more precise statement is that ebare(Λ) is the charge we would see if we collided two electrons head-on with a momentum on the order of Λ. In this collision, there is a good chance that the electrons would come within a distance of $\hbar$/Λ from each other. The larger Λ is, the smaller this distance is, and the more we penetrate past the effects of the virtual particle cloud, whose polarization ‘shields’ the electron’s charge. Thus, the larger Λ is, the larger ebare(Λ) becomes

https://arxiv.org/pdf/1609.01421.pdf

Where does the name Renormalization Group come from?

The word "renormalization" signifies that the parameters in the energy function $H'$ reflect the influence of degrees of freedom (describing the microscopic details eliminated in the coarse-graining procedure) not explicit in $H'$. The word "group" signifies that,for example, a double application of the operation with coarse graining length $L$ lattice spacings could be ralisied, in principle, by a single application with coarse-graining length $L^2$ lattice spacings.

Critical point phenomena: universal physics at large length scales by Bruce, A.; Wallace, D. published in the book The new physics, edited by P. Davies

A feature of quantum field theories that plays a special role in our considerations is the renormalization group. This group consists of symmetry transformations that in their earliest form were assumed to be associated to the procedure of adding renormalization counter terms to masses and interaction coefficients of the theory. These counter terms are necessary to assure that higher order corrections do not become infinitely large when systematic (perturbative) calculations are performed. The ambiguity in separating interaction parameters from the counter terms can be regarded as a symmetry of the theory. [11]

https://arxiv.org/pdf/1405.1548.pdf

However, take note that the renormalization group is not really a group, but only a semi-group, because coarse graining is not invertible. There are many microscopic theories that look the same after coarse-graining, i.e. after applying renormalization group transformations. Thus there is no way to invert the operation, because there are multiple possibilities.

How is the renormalization group used in QFT?

When there are no marginal variables and the least negative $\phi_{ij}$ is larger than unity in magnitude, a simple scaling description will usually work well and the Kadanoff picture almost applies. When there are no relevant variables and only one or a few marginal variables, field-theoretic perturbative techniques of the Gell-Mann-Low (1954), Callan-Symanzik or so-called "parquet diagram" varieties may well suffice (assuming the dominating fixed point is sufficiently simple to be well under- stood). There may then be little incentive for specifically invoking general RG theory. This seems, more or less, to be the current situation in QFT and it applies also in certain condensed matter problems. […] Certain aspects of the full theory do seem important because Nature teaches us, and particle physicists have learned, that quantum field theory is, indeed, one of those theories in which the different scales are connected together in nontrivial ways via the intrinsic quantum-mechanical fluctuations. However, in current quantum field theory, only certain facets of renormalization group theory play a pivotal role. High-energy physics did not have to be the way it is!

Michael Fisher in Conceptual Foundations of Quantum Field Theory, Edited by Cao

t' Hooft's 2-Loop Exact Renormalization Group Equation
Usually, the $\beta$ functions for the gauge couplings are given in the form

$$ \beta(g) = \sum a_n g^n . $$

t'Hooft noted, that by defining $g_R \equiv g + \sum r_n g^n$, we get a new coupling $g_R$ whose $\beta$ function stops at the second order, i.e. all higher orders are zero:

$$ \beta_R(g_R) = a_1 g_R + a_2 g_R^2. $$

This transformation is known as 't Hooft transformation and the corresponding renormalization scheme the 't Hooft scheme.

This scheme is only defined relative to other schemes, because we can only define the $r_n$ in terms of the $a_n$.

(Source)

't Hooft' has suggested that one can exploit this freedom in the choice of g even further and choose a new coupling parameter $g_R$ such that the corresponding $\beta(g_R) =a_1 g_R+ a_2 g_R^2$ (for the above case) and thus has only two terms in its expansion in $g_R$.

Explicit solutions for the 't Hooft transformation by N. N. Khuri and Oliver A. McBryan*

Given that the bℓ for ℓ ≥ 3 are scheme-dependent, one may ask whether it is possible to transform to a scheme in which the b ′ ℓ are all zero for ℓ ≥ 3, i.e., a scheme in which the two-loop β function is exact. Near the UV fixed point at α = 0, this is possible, as emphasized by ’t Hooft [21]. The resultant scheme, in which the beta function truncates at two-loop order is commonly called the ’t Hooft scheme [22].

https://arxiv.org/pdf/1411.6645.pdf

The nullification of higher order coefficients of the β-function is achieved by finite renormalizations of charge. They are changing the expressions for the coefficients of perturbation theory series for Green functions, evaluated in the concrete renormalization scheme, say MS-scheme. https://arxiv.org/pdf/1108.5909.pdf

Problems of the Scheme:

This observation, together with the fail to reproduce factorizable expression for the MS-scheme variant of Crewther relation leads to the conclusion that one should not use ’t Hooft prescription in the theoretical studies of the special features of gauge theories, which are manifesting themselves in the renormalization group calculations, performed at the beyond-two-loop level. In principle, this was foreseen by ’t Hooft himself in the work of Ref.[19], where he wrote “We do think perturbation theory up to two loops is essential to obtain accurate definition of the theory. But we were not able to obtain sufficient information on the theory to formulate self-consistent procedure for accurate computations”. This statement makes quite understandable the doubts on applicability of the ’t Hooft scheme in asymptotic regime [46], related to applications of the perturbative results obtained beyond-two-loop approximation. This forgotten statement of Ref.[19] is also supporting our non-comfortable feeling from the fail to reproduce factorizable expressions of the Crewther relation, explicitly obtained with the help of application of another ’t Hooft prescription - the scheme of minimal subtractions for subtracting ultraviolet divergences [16] at the level of order a 4 s corrections [13], [18]. https://arxiv.org/pdf/1108.5909.pdf

Renormalization Scheme Dependence of the Renormalization Group Equation
The beta functions for the couplings depend on the renormalization scheme.

However, this dependence starts at the three-loop level; the one-loop and two-loop terms in the beta-function are the same in all renormalization schemes!

http://bolvan.ph.utexas.edu/~vadim/classes/2009s.homeworks/ms.pdf

What is the meaning of Landau Poles?

Unfortunately, nobody has been able to carry out this kind of analysis for quantum electrodynamics. In fact, the current conventional wisdom is that this theory is inconsistent, due to problems at very short distance scales. In our discussion so far, we summed over Feynman diagrams with ≤ n vertices to get the first n terms of power series for answers to physical questions. However, one can also sum over all diagrams with ≤ n loops: that is, graphs with genus ≤ n. This more sophisticated approach to renormalization, which sums over infinitely many diagrams, may dig a bit deeper into the problems faced by quantum field theories. If we use this alternate approach for QED we find something surprising. Recall that in renormalization we impose a momentum cutoff Λ, essentially ignoring waves of wavelength less than $\hbar$/Λ, and use this to work out a relation between the the electron’s bare charge ebare(Λ) and its renormalized charge eren. We try to choose ebare(Λ) that makes eren equal to the electron’s experimentally observed charge e. If we sum over Feynman diagrams with ≤ n vertices this is always possible. But if we sum over Feynman diagrams with at most one loop, it ceases to be possible when Λ reaches a certain very large value, namely

$$ \Lambda = exp \left( \frac{3\pi}{2\alpha}+\frac{5}{6}\right) m_e c \approx e^{647} m_e c. $$ According to this one-loop calculation, the electron’s bare charge becomes in- finite at this point! This value of Λ is known as a ‘Landau pole’, since it was first noticed in about 1954 by Lev Landau and his colleagues [54].

I said that poetically speaking, the bare charge of the electron is the charge we would see if we could strip off the electron’s virtual particle cloud. A somewhat more precise statement is that ebare(Λ) is the charge we would see if we collided two electrons head-on with a momentum on the order of Λ. In this collision, there is a good chance that the electrons would come within a distance of $\hbar$/Λ from each other. The larger Λ is, the smaller this distance is, and the more we penetrate past the effects of the virtual particle cloud, whose polarization ‘shields’ the electron’s charge. Thus, the larger Λ is, the larger ebare(Λ) becomes. So far, all this makes good sense: physicists have done experiments to actually measure this effect. The problem is that ebare(Λ) becomes infinite when Λ reaches a certain huge value.

Of course, summing only over diagrams with ≤ 1 loops is not definitive. Physicists have repeated the calculation summing over diagrams with ≤ 2 loops, and again found a Landau pole. But again, this is not definitive. Nobody knows what will happen as we consider diagrams with more and more loops. Moreover, the distance $\hbar$/Λ corresponding to the Landau pole is absurdly small! […]

Quantum field theory seems to be holding up very well so far, but no reasonable physicist would be willing to extrapolate this success down to $6 × 10^{-294}$ meters, and few seem upset at problems that manifest themselves only at such a short distance scale.

https://arxiv.org/pdf/1609.01421.pdf

History

The renormalization group equations were discovered by Gell-Mann and Low in their paper Quantum Electrodynamics at Small Distances. They studied the Coulomb potential $V$ and discovered that in the high momentum limit, where the mass of the electron shouln't matter, the potential does not scale as one would expect naively from dimensional analysis. They explained this by noting that this is a result of the renormalization procedure. If we, instead define the fine structure constant $ \alpha$ simply by

$$ \alpha \equiv r V(r) ,$$

which means that $\alpha$ is simply the coefficient of $1/r$ in the Coulomb potential, there is no problem at all. The interpretation is then that $\alpha$ is scale dependend. The scale dependence is described by the famous $\beta$ functions.

In a similar analysis by Callan and Symanzik they explained the "anomaly in the trace of the energy-momentum tensor". This trace should be zero in the no-mass limit, but isn't in higher order perturbation theory. This problem came up through the studying of the scaling behaviour of higher order contributions to scattering ampliteds. Analogously, to the Coulomb potential problem described above, these also did not posses the "naive" scaling behaviour one would expect. The analogous to the Gell-Mann-Low $\beta$ functions for this problem are the famous Callan-Symanzik equations.

The common theme of both analysis is that the naive dimensional analysis breaks down, because of renormalization.

The beginning of modern field theory in Russia I would associate with the great work by Landau, Abrikosov and Khalatnikov [1]. They studied the structure of the logarithmic divergences in QED and introduced the notion of the scale dependent coupling. This scale dependence comes from the fact that the bare charge is screened by the cloud of the virtual particles, and the larger this cloud is the stronger screening we get.

https://arxiv.org/pdf/hep-th/9211140.pdf

Unfortunately, when the book on quantum field theory by Bogoliubob and Shorkov was published in the late 1950s, which I believe contained the first mention in a book of these matters, Bogoliubov and Shorkov seized on the point about the invariance with respect to where you renormalize the charge, and they introduced the term "renormalization group" to express this invariance. But what they were emphasizing, it seems to me, was the least important thing in the whole business.

It's a truism, after all, that physics doesn't depend on how you define the parameters. I think readers of Bogoliubov and Shirkov may have come into the grip of a misunderstanding that if you somehow identify a group that then you're going to learn something physicsl from it. Of, course, this is not always so. For instance when you do bookkeeping you can count the credits in black and the debits in red, or you can perform a group transformation and interchange black and red, and the rules of bookkeeping will have an invariance under that interchange. But this does not help you to make any money.

The important thing about the Gell-Mann-Low paper was the fact that they realized that quantum field theory has a scale invariance, that the scale invariance is broken by particle masses but these are negligible at very high energy or very short distances if you renormalize in an appropriate way, and that then the only thing that's breaking scale invariance is the renormalization procedure, and that one can take that into account by keeping track of the running coupling constant $\alpha_R$.

Why the Renormalization Group Is a Good Thing by Steven Weinberg

Recommended Resources:

Roadmaps

Here's a plan of how to understand the renormalization group effectively and quickly:

  1. First, have a look at http://philosophy.wisc.edu/forster/Percolation.pdf
  2. Then read http://jakobschwichtenberg.com/renormalization-group-flow/
  3. Then, the best complete introduction can be found in Critical point phenomena: universal physics at large length scales by Bruce, A.; Wallace, D. published in the book The new physics, edited by P. Davies
  4. Afterwards read https://www.andrew.cmu.edu/user/kk3n/found-phys-emerge.pdf which explains lucidly many of the most important "advanced" concepts.
  5. See also "Why the Renormalization Group Is a Good Thing" by S. Weinberg
  6. Critical Phenomena for Field Theorists by Steven Weinberg
  7. Also the video course: Introduction to Renormalization by Simon DeDeo is highly recommended to understand how the renormalization group can be used in other fields than physics.
  8. http://www.damtp.cam.ac.uk/user/tong/sft.html
  9. A hint of renormalization by B. Delamotte