Non-Perturbative QFT
Why is it interesting?
Calculation methods beyond the usual perturbation expansion are especially important in QCD, because the coupling becomes large at large distances and therefore the expansion is useless.
Since QCD is strongly coupled and therefore non-perturbative at low energies, we expect the vacuum to be populated by strong fields. (This is in contrast to standard QED, for example, where the vacuum contains mostly zero-point fluctuations, i.e. weakly interacting electron-positron pairs and photons which can be handled perturbatively.) […] Strong fields can contain a very large number of quanta, and those quanta can become coherent and render the corresponding action large compared to ℏ. In other words, such fields behave (semi-) classically since quantum fluctuations are of O (ℏ) and thus contribute only relatively small corrections. The above reasoning suggests that insight into the vacuum fields of QCD may be gained from a semiclassical perspective.
Layman
Instead of using the usual perturbation expansion one can try to find solutions to the classical field equations and use these as starting points for calculations.
However, in contrast to electromagnetism, the classical field equations of general Yang-Mills theory are highly complicated. While the Maxwell equations are linear and can be easily solved (the solutions describe electromagnetic waves), the analogous Yang-Mills equations are non-linear and complicated to solve.
This complicated structure gives rise to many interesting phenomena that can not be described by a perturbative approach. The most important example is the structure of the QCD vacuum.
Non-perturbative methods are also approximation methods, but a different kind of approximation. Instead small perturbations, described by an expansion in the gauge coupling, one considers semi-classical approximations. Non-perturbative methods are important to describe scenarios where the usual perturbation theory is not applicable. A good example are tunneling processes. For example, the QCD vacuum posses an infinite number of ground states with equal energy. With perturbation theory we can only describe small perturbations around such a minimum. However in a quantum theory, there can be tunneling processes between minimums of a potential. Such processes are called instantons. A perturbative approach would never notice anything about the other minimas and is therefore not able to describe the true ground state, which is a superpositon of all "classical" ground states, with tunneling processes connecting them. At first it is confusing why such processes are described by a semi-classical approximation, because there is no tunneling in classical physics. However, the semi-classical approach is merely a trick to identify the dominant contributions to the path integral. We focus on these dominant contributions, because we can not compute the path integral exactly. We call the saddle points of the action classical paths and these dominante the sum over all possible paths. Another trick to make this idea work, is to redefine the time as $i t$, i.e. make the time complex. This is necessary, because there is no tunneling in classical physics. By making the time imaginary, in some sense, we flip the potential upside down, and thus classical paths become possible. Another way to see why imaginary times are useful to describe tunneling processes, is to remember the usual quantum mechanical situation of tunneling through a potential barrier. Outside of the barrier, the wave function oscillated $\mathrm{e}^{i\omega t}$. However, in the potential the wave function is damped exponentially:$\mathrm{e}^{- \omega t}$. The connection between a "usual" wave function, and a tunneling wave function is therefore $t \to i t$. These points are described in the following sections in more detail.
Student
- Advanced Topics in Quantum Field Theory by M. Shifman
Researcher
Examples
- Example1
- Example2:
FAQ
- Why do we use a semi-classical approximation?
-
Classical solutions dominate the path integral. (Source: page 416 in Topological Solitons by Manton, Sutcliff)
The corresponding quantum field theory (including the quarks) determines the structure of the QCD vacuum, i.e. the unique state of lowest energy on which the Fock space is built. Since QCD is strongly coupled and therefore non-perturbative at low energies, we expect the vacuum to be populated by strong fields. (This is in contrast to standard QED, for example, where the vacuum contains mostly zero-point fluctuations, i.e. weakly interacting electron-positron pairs and photons which can be handled perturbatively.) […] Strong fields can contain a very large number of quanta, and those quanta can become coherent and render the corresponding action large compared to ℏ. In other words, such fields behave (semi-) classically since quantum fluctuations are of O (ℏ) and thus contribute only relatively small corrections. The above reasoning suggests that insight into the vacuum fields of QCD may be gained from a semiclassical perspective.
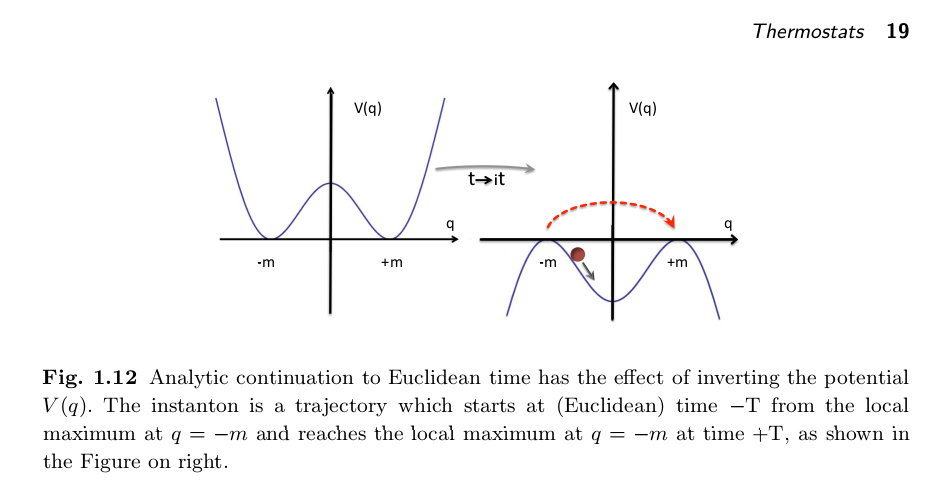
Usually in QFT we use perturbation theory. However, there are phenomena that can not be described by this method. A good example is the double well potential $V(q)=\frac{\lambda}{4!}(q^2-a^2)^2$:
There are two classical ground states. However, in the usual perturbation approach, we ignore this fact and expand $V$ around one of these minimas. The potential then looks exactly as the potential of the harmonic oscillator about that minimum plus anharmonic terms (cubic, quartic). The perturbation approach then yields possible wave functions and energies. However, we never see any evidence of the second minimum. Of course, it makes no difference which minimum we choose. Equally, we could expand around the other minimum. The energy levels are exactly the same in all orders of perturbation theory. However through perturbative effects there is only one true ground state and not two degenerate ground states which is suggested by perturbation theory. This shows that perturbation theory fails to describe all possible phenomena. (Source: http://www.weizmann.ac.il/particle/perez/Courses/QMII16/TA4.pdf)
The approximation method that is used in such situations is called semi-classical approximation or the method of steepest descend. See page 2 in http://www.weizmann.ac.il/particle/perez/Courses/QMII16/TA4.pdf for an illustration of the idea behind this method.
As far as I know there is currently no better approach to deal with such effects. For example, QCD can not be solved exactly and therefore, we need to use approximation methods. Perturbation theory does not work and thus we need another approximation method. At the moment, non-perturbative effects are described using the semi-classical approximation. However this method also has limitations.
[Instanton physics] is both exciting and frustrating. It is exciting because, at last, a substantial body of evidence shows that the original vision of the role of instantons in QCD is borne out in nature. However, as will be clear below, it is also frustrating because of intrinsic limits to the precision with which one can apply ultimately semiclassical concepts.
Instantons, the QCD Vacuum, and Hadronic Physics by J. W. Negele
- Why do we use a imaginary time?
-
Tunneling processes can not be described with perturbation theory. Instead one employs a semi-classical approach. This works, because we can describe a tunneling trajectory as a classical trajectory in imaginary time. This can be seen by considering the following example:
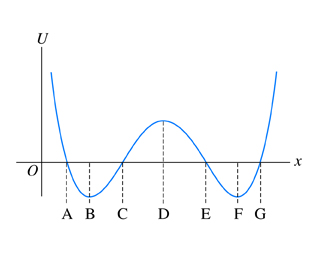
Consider a particle with energy $E$ sitting in the minimum of a double well potential, for example, at B in the following picture:
The classical energy momentum relation is: \begin{equation} E=\frac{m}{2}\dot{x}^{2}+V \quad \Rightarrow \quad \dot{x}=\sqrt{\frac{2(E-V)}{m}} \end{equation}
We can the use separation of variables for $\dot{x} = \frac{dx}{d\tau}$:
\begin{equation} \sqrt{\frac{m}{2}}\frac{dx}{\sqrt{(E-V)\left( x\right) }}=d\tau, \end{equation} and then integrate the equation to find the trajectory
\begin{align} \int_{B}^{F}\sqrt{\frac{m}{2}}\frac{dx}{\sqrt{(E-V)\left( x\right) }}&= \int_{\tau_1}^{\tau_2}d\tau \notag \\ \int_{B}^{F}\sqrt{\frac{m}{2}}\frac{dx}{\sqrt{(E-V)\left( x\right) }}&= \tau_1 - \tau_2 . \end{align}
Classically there is no solution if $V>E$, because then the time becomes complex through the negative root above. However, we know that in Quantum Mechanics tunneling through such a potential barrier is possible. Therefore, we see here that formally such a trajectory through a forbidden region corresponds to a classical trajectory in imaginary time.
Another point of view is that if we work with $t \rightarrow i \tau$, we flip the potential upside down: $V \rightarrow -V$.
Since no classical trajectory can be associated to barrier penetration, one may wonder how it is possible to evaluate such effects in the semi-classical limit. Actually, it has been noticed that, formally, barrier penetration has a semi-classical interpretation in terms of classical particles moving in imaginary time. […] To calculate instanton contributions at leading order, one must master two problems that are increasingly difficult: find the saddle points by solving classical equations, expand the integrand around the saddle point and evaluate the path integral at leading order by integrating over Gaussian fluctuations.
http://ipht.cea.fr/Docspht/articles/t11/211/public/2011_Zinn-Justin_all_lectures.pdf
The seemingly artificial analytical continuation to imaginary times has allowed us to identify those paths whose neighborhoods give the dominant contributions to the path integral for a tunneling process in the semiclassical limit, and to evaluate this path integral to O (~) in the saddle-point approximation. In more physical terms the situation can be described as follows: for tunneling problems there exist no minimal-action trajectories (i.e. classical solutions) with the appropriate boundary conditions in real time. Therefore all trajectories between those boundary conditions (over which we sum in the real-time path integral) interfere highly destructively. Still, their net effect can be approximately gathered in a finite number of regions in function space, namely those in the neighborhood of the saddle points in imaginary time. In other words, while the tunneling amplitudes would have to be recovered at real times from a complex mixture of non-stationary paths (a forbidding task in practice), they are concentrated around the classical paths in imaginary time, and are therefore accessible to the saddlepoint approximation. The destructive interference at real times leaves a conspicuous trace, however, namely the exponential suppression of (2.40) due to the Gamov factor exp (−SE/h), which is typical for tunneling amplitudes.
To bring the tunneling interpretation into clearer view, it is helpful to pass to the imaginary time picture, i.e. to discuss $<n'|e^{-HT}|n>$ instead of $<n'|e^{-HTi}|n>$, The reason for this is that we know from experience with ordinary quantum mechanics that imaginary time solutions of the classical eguations of motion can be used to obtain a WKB (or small H) treatment of barrier penetration problems. In real time a classically forbidden process defines no stationary path which dominates the functional integral and there is no simple way to study tunneling. […] Since the action is positive definite, the dominant history is the one of minimum action consistent with the boundary conditions. Such a path satisfies all the Euclidean Yang-Mills equations - except the Gauss' law constraint. Upon varying the end points of the Ai path history, one will finally pick out the path which satisfies the constraint as well. This path is guaranteed to have the absolute minimum action consistent with the constraint that it describe a transition n ~ n' and satisfies the full set of Euclidean Yang-Hills equations. A rather large class of Euclidean Yang-Hills solutions are known by now, 19 but we need only discuss the original one of Belavin et al. out of which, in a sense, all the others are constructed.
Toward a Theory of the Strong Interactions by Curtis G. Callan et. al.
- What is the role of the path integral formalism for non-perturbative methods?
-
As mentioned above, we use a semi-classical approach to investigate effects that are not captured by the usual perturbative approach. This semi-classical approximation can be realized nicely by using Feynman's path integral formalism, which, in addition, can also be used in quantum field theory.
Most of the time it is impossible to carry out the summation over all paths. Therefore, in practice one looks for those paths that dominate the summation, i.e. yield the largest contributions. The paths that yield are the extremal points of the action and these paths are exactly what we usually call the classical paths. This can be understand nicely, for example, by considering "cornu spirals".
Thus, we can approximate the highly complicated sum over all paths by just keeping these dominant contributions and small fluctuations about them. However, as already mentioned above, there are no classical paths that describe, for example, the tunneling through a potential barrier.
The clever trick one then employs is to continue the time variable to imaginary values. This enables us to find those path that dominate the sum over all paths and thus find a sensible approximation.
Another way of looking at this trick is that the potential gets flipped. We start with the action
$$ S[x]^{t_2}_{t_1} = \int^{t_2}_{t_1} \left[ \frac{1}{2m}\left(\frac{dx}{dt}\right)^2-V(x) \right] dt $$
and then change the integration variable by defining $t= -i\tau$:
$$ S[x]^{-i\tau_2}_{-i\tau_1} = \int^{-i\tau_2}_{-i\tau_1} \left[ \frac{1}{2m}\left(\frac{dx}{-id\tau}\right)^2-V(x) \right] (-i d\tau) .$$
We then define the Euclidean action $S_E$ as
$$ S_E [x]^{\tau_2}_{\tau_1} \equiv i S[x]^{t_2}_{t_1} $$
and thus have
$$ S_E [x]^{\tau_2}_{\tau_1} = \int^{\tau_2}_{\tau_1} \left[ \frac{1}{2m}\left(\frac{dx}{d\tau}\right)^2+V(x) \right] d\tau $$
where $\tau$ is called the Euclidean time. This is exactly the action for a "mirror image" of the problem that we started with, i.e. the same problem with a flipped potential $ -V(x)$. The potential barrier has become a well and therefore, now there exist classical paths!
As mentioned above, we investigate this situation to find the classical paths that dominate the sum over all paths. In the approximate solution, we must at the end switch back to the correct time by using $\tau \to i t$.
(Source: page 315 in An Introduction to Gauge Theories and Modern Particle Physics, Vol 2 by Elliot Leader,Enrico Predazzi)
The most useful approach to the quantization of gauge theories appears to be Feynman's path integral method. From a geometric point of view, the path integral has the advantage of being able to take into account the global topology of the gauge potentials, while the canonical perturbation theory approach to quantization is sensitive only to the local topology.
http://home.fnal.gov/~leonardo/physicsnotes/notes/NotesInstantons.pdf