SU(3)

Intuitive

The Lie group $SU(3)$ describes abstract "rotations" in a space with three complex dimensions. A "rotation" is characterized by eight abstract "angles" or parameters.

Concrete

Representations

The diagram below shows the defining (3-dimensional) representation of $SU(3)$ in its upper branch and the 8-dimensional adjoint representations of the same group in its lower branch. The adjoint representation can be rewritten such that it acts on 8-dimensional vectors (as opposed to 3x3 matrices) by regular matrix-vector multiplication.

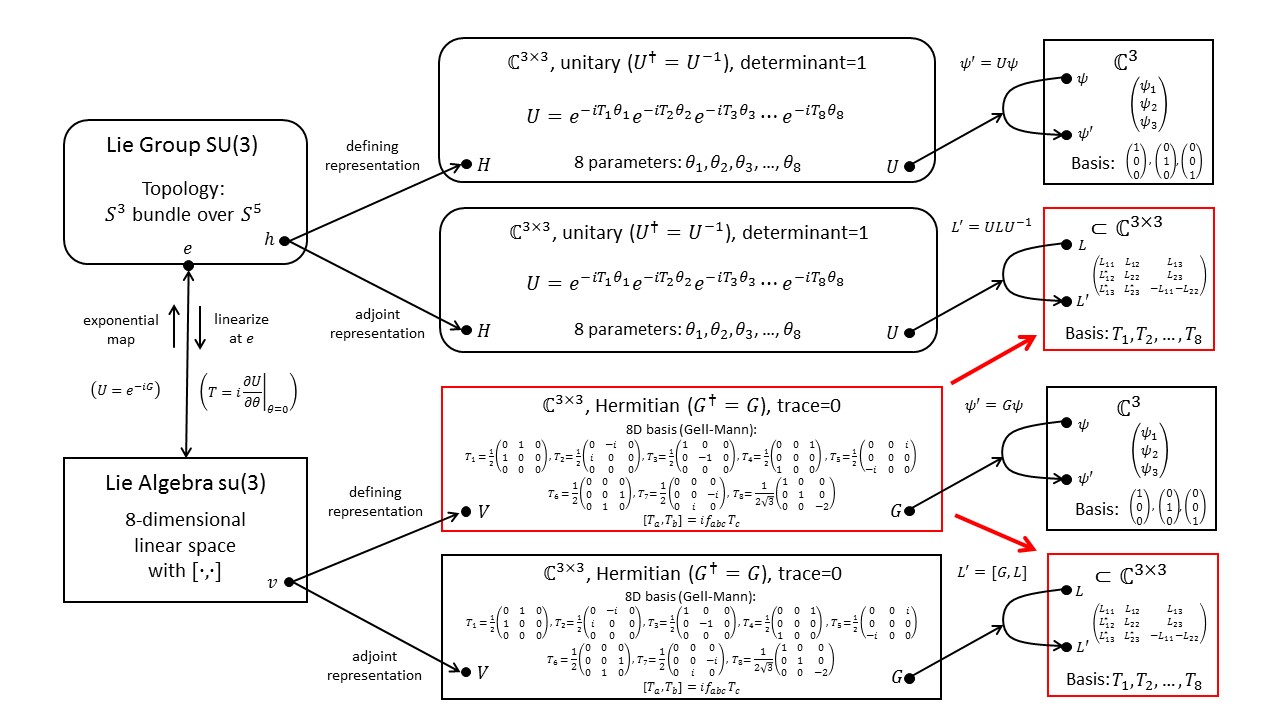
For more groups and their representations see Fun with Symmetry.

Abstract

Why is it interesting?

$SU(3)$ is at the heart of the so-called "eightfold way", a scheme that organizes the large "zoo" of hadron particles into neat geometrical patterns (octets and decuplets).

$SU(3)$ is also the gauge group of the strong nuclear interaction. It describes how particles with "color charge" (quarks and gluons) interact.