Dual Representation

Intuitive

For any representation, there is a dual representation, which acts on the dual vector space instead of the original vector space. The elements of the dual vector space are covectors, which are linear functions from the vectors to scalars.

For representations with orthogonal matrices, the dual representation is the same as the original representation.

For unitary representations, the dual representation is the same as the complex-conjugate representation.

The dual of the defining representation of the Lorentz group is the parity-reversed representation.

Concrete

Example

The diagram below shows the defining representation of $SU(2)$ in its upper branch. To construct the dual representation, we let it act on the dual vector space, that is, the space of covectors. In this example, the dual representation is the same as the complex-conjugate representation ($\tilde{U}=U^*$). Moreover, the defining and complex-conjugate representations of $SU(2)$ are equivalent, that is, there is a similarity transformation that takes one to the other.

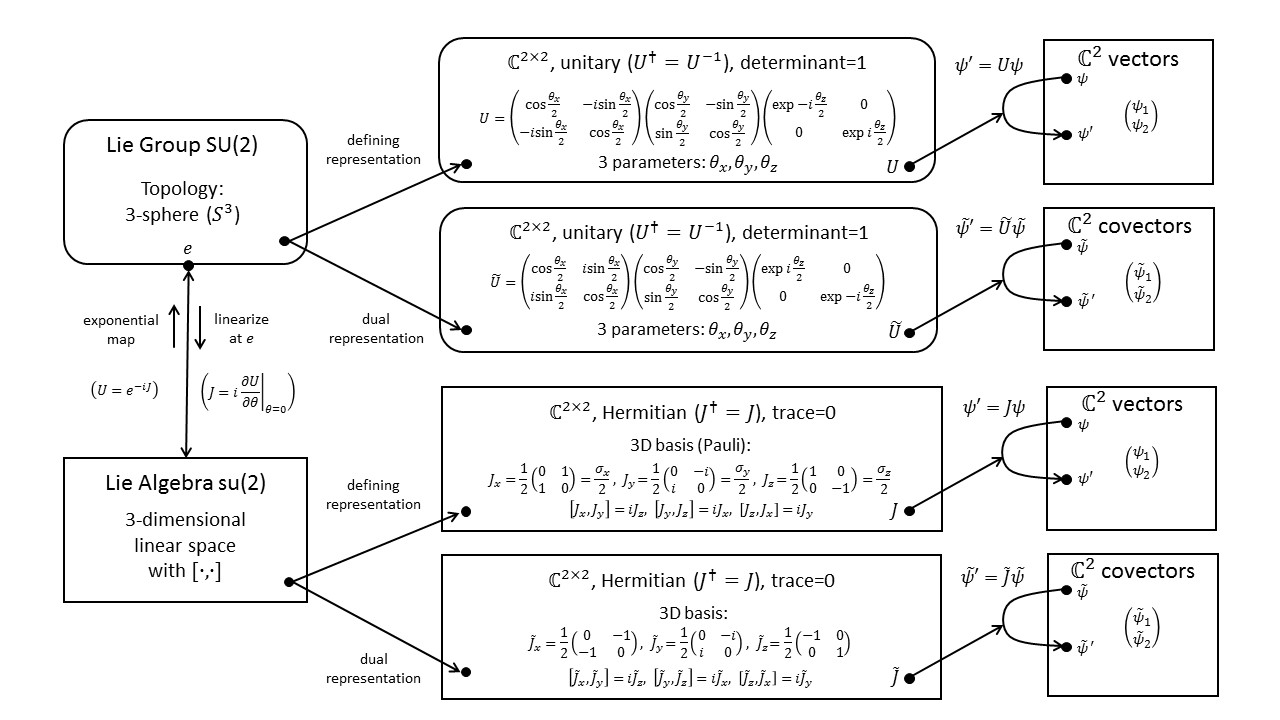
For a more detailed explanation of this diagram see Fun with Symmetry.

Abstract

Why is it interesting?